Как решить модель Лоренца 96 методом Рунге – Кутты?
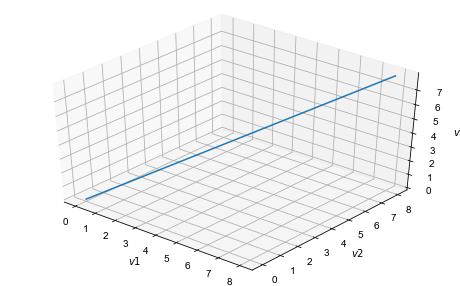
Я написал приведенный ниже код для решения модели Лоренца 96 с использованием метода Рунге-Кутты, но результаты ненадежны, как видно на рисунке ниже:
Правильное соотношение между тремя переменными выглядит следующим образом:
Как я могу изменить код, чтобы решить проблему правильно? Для получения дополнительной информации о Lorenz 96 см. Модель Lorenz 96 в Википедии .
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
###############################################################################
# Define Lorenz 96 function
# These are our constants
N = 3 # Number of variables
F = 8 # Forcing
def L96(v, t):
"""Lorenz 96 model with constant forcing"""
# Setting up vector
dv_dt = np.zeros(N)
# Loops over indices (with operations and Python underflow indexing handling edge cases)
for i in range(N):
dv_dt[i] = (v[(i + 1) % N] - v[i - 2]) * v[i - 1] - v[i] + F
return dv_dt
#define the given range t
t0=0
tn=100
h=0.005
#define number of steps (n)
time_range=np.arange(t0, tn, h)
# preallocate space
v0=np.zeros((len(time_range)+1, 1, N))
t=np.zeros(len(time_range)+1)
v0[0][0][0] += 0.01 # Add small perturbation to the first variable
L96(v0[0][0],0)
# Solve Runge-Kutta
for i in range (len(time_range)):
print(i)
dv_dt=L96(v0[i][0],t[i])
k1=dv_dt[0]
l1=dv_dt[1]
m1=dv_dt[2]
k2=L96([v0[i][0][0]+0.5*k1*h,v0[i][0][1]+0.5*l1*h,v0[i][0][2]+0.5*m1*h],t[i]+h/2)
l2=L96([v0[i][0][0]+0.5*k1*h,v0[i][0][1]+0.5*l1*h,v0[i][0][2]+0.5*m1*h],t[i]+h/2)
m2=L96([v0[i][0][0]+0.5*k1*h,v0[i][0][1]+0.5*l1*h,v0[i][0][2]+0.5*m1*h],t[i]+h/2)
k3=L96([v0[i][0][0]+0.5*k2[0]*h,v0[i][0][1]+0.5*l2[0]*h,v0[i][0][2]+0.5*m2[0]*h],t[i]+h/2)
l3=L96([v0[i][0][0]+0.5*k2[1]*h,v0[i][0][1]+0.5*l2[1]*h,v0[i][0][2]+0.5*m2[1]*h],t[i]+h/2)
m3=L96([v0[i][0][0]+0.5*k2[2]*h,v0[i][0][1]+0.5*l2[2]*h,v0[i][0][2]+0.5*m2[2]*h],t[i]+h/2)
k4=L96([v0[i][0][0]+0.5*k3[0]*h,v0[i][0][1]+0.5*l3[0]*h,v0[i][0][2]+0.5*m3[0]*h],t[i]+h/2)
l4=L96([v0[i][0][0]+0.5*k3[1]*h,v0[i][0][1]+0.5*l3[1]*h,v0[i][0][2]+0.5*m3[1]*h],t[i]+h/2)
m4=L96([v0[i][0][0]+0.5*k3[2]*h,v0[i][0][1]+0.5*l3[2]*h,v0[i][0][2]+0.5*m3[2]*h],t[i]+h/2)
v0[i+1][0][0] = v0[i][0][0] + h*(k1 +2*k2[0] +2*k3[0] +k4[0])/6 # final equations
v0[i+1][0][1] = v0[i][0][1] + h*(l1 +2*k2[1] +2*k3[1] +k4[1])/6
v0[i+1][0][2] = v0[i][0][2] + h*(m1+2*k2[2] +2*k3[2] +k4[2])/6
t[i+1]=time_range[i]
###############################################################################
v_array=np.array(v0)
v_array.shape
v1=v_array[:,0][:,0]
v2=v_array[:,0][:,1]
v3=v_array[:,0][:,2]
fig, (ax1, ax2) = plt.subplots(1, 2,constrained_layout=True,figsize=(10, 4))
ax1.plot(v1,v3)
ax1.set_title('v1 vs v2')
ax2.plot(v2,v3)
ax2.set_title('v2 vs v3')
# Plot 3d plot of v1,v2, and v3
from mpl_toolkits import mplot3d
fig = plt.figure(figsize=(8, 5))
ax = plt.axes(projection='3d', elev=40, azim=-50)
ax.plot3D(v1, v2, v3)
ax.set_xlabel('$v1$')
ax.set_ylabel('$v2$')
ax.set_zlabel('$v3$')
plt.show()
1 ответ
Я не совсем уверен, какова ваша мотивация снова разорвать векторизацию на строки для отдельных компонентов. В любом случае это неправильно. Ваша временная петля должна быть такой же простой, как
for i in range(len(time)-1):
v[i+1] = RK4_step(lambda t,y:L96(y,t),time[i],v[i],time[i+1]-time[i])
где метод stepper - это просто код кулинарной книги
def RK4_step(f,t,y,h):
k1 = h*f(t,y)
k2 = h*f(t+0.5*h, y+0.5*k1)
k3 = h*f(t+0.5*h, y+0.5*k2)
k4 = h*f(t+h, y+k3)
return y+(k1+2*k2+2*k3+k4)/6
Таким образом, нет жесткого ограничения на 3 компонента, компоненты кода универсальны,
L96Функцию можно использовать с любым числом численных решателей из библиотек или самостоятельно реализованных, степпер и временная петля для RK4 действительны для любой другой системы дифференциальных уравнений.
Обратите внимание, что в примере из Википедии есть компоненты, где 3D-график строится из первых 3-х из них. За
N=3вы действительно получаете сходимость к фиксированной точке, которая выглядит как прямая линия, для
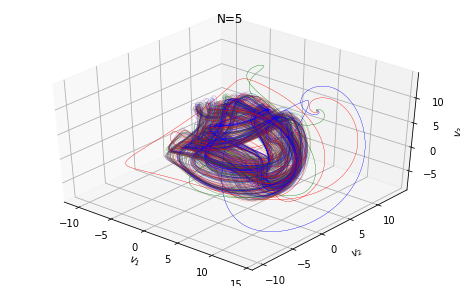
N=4кажется, что существует предельный цикл, только для
N=5решение начинает выглядеть хаотичным.
Наличие трехмерного массива имеет смысл при одновременном вычислении нескольких траекторий. (Но только с методами с фиксированным шагом или если гарантируется, что они остаются близко друг к другу, в противном случае управление размером шага будет неподходящим для большинства траекторий большую часть времени.) Полный сценарий для этой адаптации гласит:
# Define Lorenz 96 function
# These are our constants
N = 4 # Number of variables
F = 8 # Forcing
def L96(t, v):
"""Lorenz 96 model with constant forcing"""
# Setting up vector
dv_dt = 0*v
# Loops over indices (with operations and Python underflow indexing handling edge cases)
for i in range(N):
dv_dt[i] = (v[(i + 1) % N] - v[i - 2]) * v[i - 1] - v[i] + F
return dv_dt
#define the given range t
t0=0
tn=100
h=0.005
#define number of steps (n)
time = np.arange(t0, tn, h)
v = np.zeros([len(time),N,3], float)
v[0] +=F
v[0,0,0] -= 0.005
v[0,0,1] += 0.005
v[0,0,2] += 0.01
for i in range(len(time)-1):
v[i+1] = RK4_step(L96,time[i],v[i],time[i+1]-time[i])
# Plot 3d plot of first 3 coordinates
from mpl_toolkits import mplot3d
fig = plt.figure(figsize=(8, 5))
ax = plt.axes(projection='3d', elev=40, azim=-50)
ax.plot3D(v[:,0,0], v[:,1,0], v[:,2,0],'g', lw=0.2)
ax.plot3D(v[:,0,1], v[:,1,1], v[:,2,1],'r', lw=0.2)
ax.plot3D(v[:,0,2], v[:,1,2], v[:,2,2],'b', lw=0.2)
ax.set_xlabel('$v_1$')
ax.set_ylabel('$v_2$')
ax.set_zlabel('$v_3$')
ax.set_title(f"N={N}")
plt.show()