Python, учитывая неявное уравнение, найти точки в этом уравнении?
Контекст: преобразование
.iges к
.vtk.
У меня есть следующее уравнение
Ax^2+Bxy+Cy^2+Dx+Ey+F=0 представляющий коническое сечение.
Параметры
A~Fданы. Я хочу найти точки на конической секции , чтобы я мог соединить их линиями и создать сетку.
Причина, по которой мне нужны очки, а не просто использовать
matplotlib Ellipse потому что я создаю сетку, а не сюжет.
Он находится в трехмерном пространстве, но сначала я получаю точки на плоскости xy и использую аффинное преобразование, чтобы отправить его в 3 dim.
Вопрос:
How do I find points given an implicit equation?
2 ответа
Чтобы не тратить на это слишком много времени, я написал некоторый код, который, кажется, обрабатывает общие эллипсы. Его можно расширить для других коник, в зависимости от того, что необходимо. Код принимает коэффициенты общего квадратного уравнения эллипса и количество желаемых точек, которые должны быть сгенерированы на эллипсе, и генерирует набор точек на эллипсе.
import numpy as np
def equation(conic, points):
'''
equation of a conic with coefficients 'conic'
applied to a matrix number_of_points x 3 whose each row is the coordinates
of each point
'''
c = np.array(conic)
x = np.array([points[:,0]**2, points[:, 0]*points[:,1], points[:,1]**2, points[:,0], points[:,1], np.ones(points.shape[0])])
return c.dot(x)
def equation_to_matrix(eq):
'''
eq[0]*x**2 + eq[1]*x*y + eq[2]*y**2 + eq[3]*x + eq[4]*y + eq[5] = 0
'''
return np.array([[2*eq[0], eq[1], eq[3]],
[ eq[1], 2*eq[2], eq[4]],
[ eq[3], eq[4], 2*eq[5]]]) / 2
def solve_quadratic(a, b, c):
'''
solves
ax^2 + bx + c = 0
'''
D = b**2 - 4*a*c
D = np.sqrt(D)
return (-b-D)/(2*a), (-b+D)/(2*a)
def eigen2(S):
'''
solves the eigen-decomposition problem
for a 2x2 symmetric matrix
'''
k1, k2 = solve_quadratic(1, -S[0,0]-S[1,1], S[0,0]*S[1,1] - S[0,1]*S[1,0])
u1 = np.array([-S[0,1], S[0,0]-k1, 0])
u1 = u1 / np.sqrt(u1.dot(u1))
u2 = np.array([-u1[1], u1[0], 0])
return np.array([k1, k2]), np.array([u1, u2, np.array([0,0,1])]).T
def center(conic_matrix):
center = np.linalg.solve(conic_matrix, np.array([0,0,1]))
return center/center[2]
def find_rotation_and_translation(conic_matrix):
'''
conic = c[0]x^2 + c[1]*xy + c[2]*y^2 + c[3]*x + c[4]*y + c[5] = 0
the result is rotation U such that U.T C U = diag
'''
k, U = eigen2(conic_matrix)
U[:,2] = center(conic_matrix)
return U, k
def find_transform(conic):
C = equation_to_matrix(conic)
U, k = find_rotation_and_translation(C)
C = (U.T).dot(C.dot(U))
C = - C / C[2,2]
k = np.array([1/np.sqrt(C[0,0]), 1/np.sqrt(C[1,1]), 1])
return U.dot(np.diag(k))
def generate_points_on(conic, num_points):
'''
conic = [c[0], c[1], c[2], c[3], c[4], c[5]]
coefficients of the qudaratic equation:
conic: c[0]x^2 + c[1]*xy + c[2]*y^2 + c[3]*x + c[4]*y + c[5] = 0
result is the affine transformation (scaling, rotation, translation)
that maps the unit circle to the ellipse defined by the coefficients
'conic'
'''
cos_ = np.cos(2*np.pi* np.arange(0, num_points)/ num_points)
sin_ = np.sin(2*np.pi* np.arange(0, num_points)/ num_points)
U = find_transform(conic)
points = np.array([cos_, sin_, np.ones(num_points)])
return ((U.dot(points)).T)[:,[0,1]]
'''
Test:
'''
'''
Ellipse with equation whose coefficients are in the list E.
The ellipse has semi-major axes 2 and 1,
it is rotated 60 deg from the horizontal,
and its center is at (1, 4)
'''
E = [ 3.25, -2.59807621, 1.75, -23.40192379, 6.89230485, 39.35769515]
'''
U maps points from unit circle to points on E
'''
U = find_transform(E)
print(U)
'''
the set of points on the ellipse E
'''
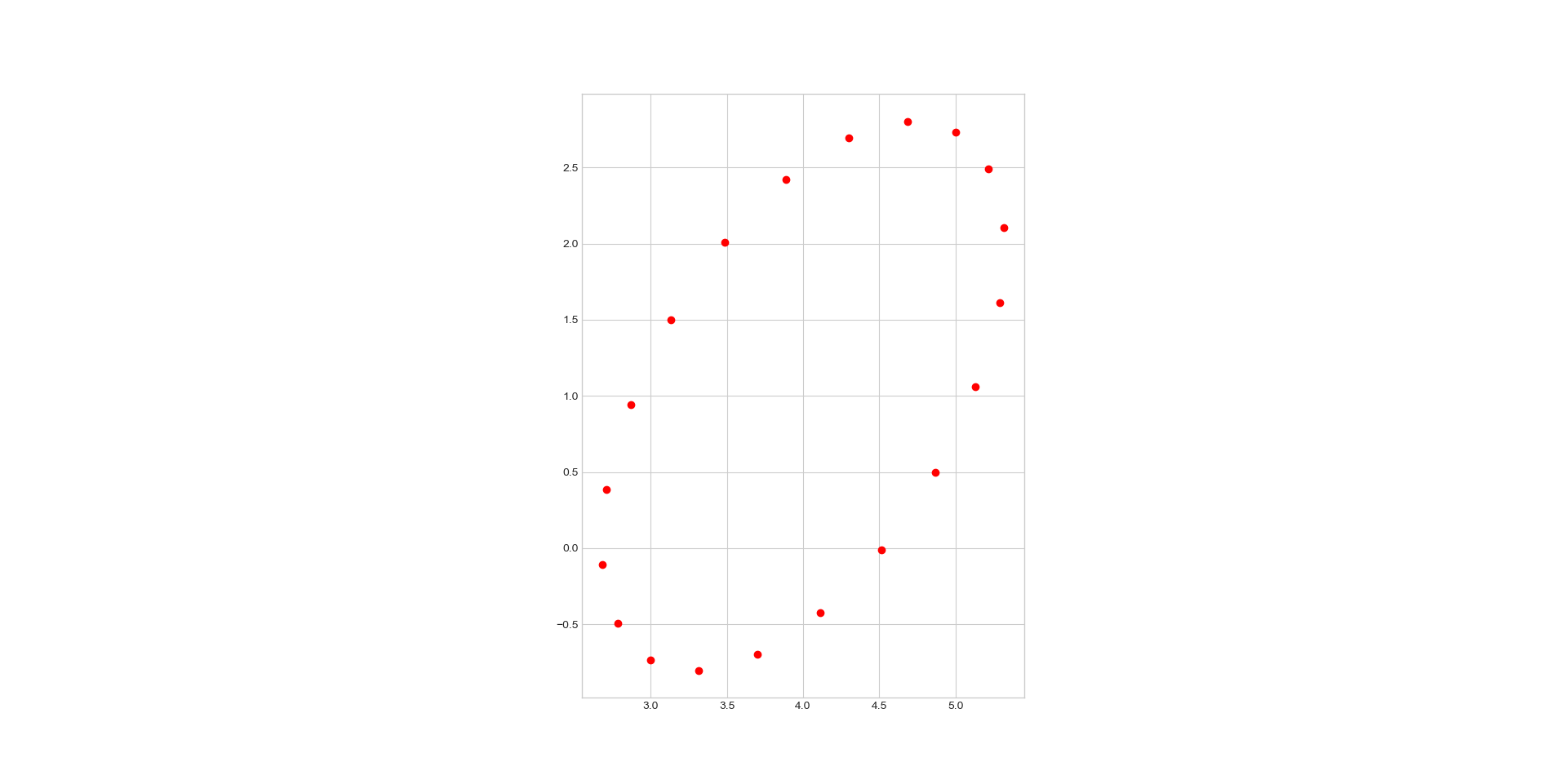
p = generate_points_on(E, num_points = 20)
print(p)
'''
check that the points p lie on the ellipse E
'''
print(equation(E, p).round(10))
'''
plot
'''
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(p[:,0], p[:,1], 'ro')
ax.set_aspect('equal')
plt.show()
Код ниже обрабатывает случай гиперболы. Он в значительной степени адаптирует код отсюда
import numpy as np
import matplotlib.pyplot as plt
def equation_to_matrix(eq):
'''
eq[0]*x**2 + eq[1]*x*y + eq[2]*y**2 + eq[3]*x + eq[4]*y + eq[5] = 0
'''
return np.array([[2*eq[0], eq[1], eq[3]],
[ eq[1], 2*eq[2], eq[4]],
[ eq[3], eq[4], 2*eq[5]]]) / 2
def hyp_params_from_general(coeffs):
# get the matrix of the quadratic equation
Aq = equation_to_matrix(coeffs)
# get the matrix of the quadratic form A33
A33 = Aq[:2, :2]
# determinant of A33
detA33 = np.linalg.det(A33)
if detA33 > 0:
raise ValueError('coeffs do not represent a hyperbola: det A33 must be negative!')
# get the center
x0 = -np.linalg.det(np.array([Aq[:2, 2], Aq[:2, 1]]).T) / detA33
y0 = -np.linalg.det(np.array([Aq[:2, 0], Aq[:2, 2]]).T) / detA33
# The semi-major and semi-minor axis lengths (these are not sorted).
# get discriminant of the conic section
delta = np.linalg.det(Aq)
# get the eigenvalues
k1, k2 = np.linalg.eigvals(A33)
k1isk2 = np.isclose(k1/k2, -1)
ap = np.sqrt(abs(delta/k1/detA33))
bp = np.sqrt(abs(delta/k2/detA33))
# Eccentricity.
fac = np.sqrt((Aq[0, 0] - Aq[1, 1])**2 + Aq[0, 1]**2)
if delta < 0:
nu = 1
else:
nu = -1
e = np.sqrt(2*fac/(nu*(Aq[0, 0] - Aq[1, 1]) + fac))
# slope of the asymptotes
if Aq[0, 0] == Aq[1, 1] and k1isk2:
m1 = 0.
m2 = np.nan
else:
m1 = Aq[0, 0]/(-Aq[0, 1] - np.sqrt(-detA33))
m2 = Aq[0, 0]/(-Aq[0, 1] + np.sqrt(-detA33))
# Sort the semi-major and semi-minor axis lengths but keep track of
# the original relative magnitudes of width and height.
width_gt_height = True
if ap < bp and not k1isk2:
width_gt_height = False
ap, bp = bp, ap
# The angle of anticlockwise rotation of the major-axis from x-axis.
if Aq[0, 1] == 0:
phi = 0 if Aq[0, 0] < Aq[1, 1] else np.pi/2
elif Aq[0, 0] == Aq[1, 1]:
phi = np.pi/4 # would divide by zero and arctan(inf) -> pi/4
if m1 > 0 and m2 > 0:
width_gt_height = True
else:# Aq[0, 0] > Aq[1, 1]:
phi = np.arctan(2*Aq[0, 1]/(Aq[0, 0] - Aq[1, 1])) / 2
if not width_gt_height:
# Ensure that phi is the angle to rotate to the semi-major axis.
phi += np.pi/2
phi = phi % np.pi
return x0, y0, ap, bp, phi, e, m1, m2, width_gt_height
def get_hyperbola_pts(params, npts=100, tmin=-1, tmax=1):
x0, y0, ap, bp, phi, m1, m2 = params
# A grid of the parametric variable, t.
t = np.linspace(tmin, tmax, npts)
# points
x = x0 + ap * np.cosh(t) * np.cos(phi) - bp * np.sinh(t) * np.sin(phi)
y = y0 + ap * np.cosh(t) * np.sin(phi) + bp * np.sinh(t) * np.cos(phi)
# asymptotes
ya1 = y0 + m1*(x - x0)
ya2 = y0 + m2*(x - x0)
return x, y, ya1, ya2
if __name__ == '__main__':
coeffs = [1., 6., -2., 3., 0., 0.]
x0, y0, ap, bp, phi, e, m1, m2, width_gt_height = hyp_params_from_general(coeffs)
print('x0, y0, ap, bp, phi, e, m1, m2, width_gt_height = ', x0, y0, ap, bp, phi, e, m1, m2)
x_, y_, ya1, ya2 = get_hyperbola_pts((x0, y0, ap, bp, phi, m1, m2), npts=250, tmin=-2, tmax=3)
fig, ax = plt.subplots(figsize=(16, 9))
ax.plot(x_, y_, marker='.', linewidth=0.5, c='r')
ax.plot(x_, ya1, marker='.', linewidth=0.2, c='b')
ax.plot(x_, ya2, marker='.', linewidth=0.2, c='b')
ax.grid(True, linestyle='--')