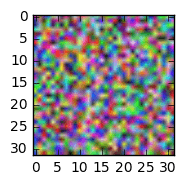Это правильный способ отбеливания изображения в Python?
Я пытаюсь zero-center а также whitenCIFAR10 набор данных, но результат, который я получаю, выглядит как случайный шум!Cifar10 набор данных содержит 60,000 цветные изображения размера 32x32, Учебный набор содержит 50,000 и тестовый набор содержит 10,000 изображения соответственно.
Следующие фрагменты кода показывают процесс, который я сделал для отбеливания набора данных:
# zero-center
mean = np.mean(data_train, axis = (0,2,3))
for i in range(data_train.shape[0]):
for j in range(data_train.shape[1]):
data_train[i,j,:,:] -= mean[j]
first_dim = data_train.shape[0] #50,000
second_dim = data_train.shape[1] * data_train.shape[2] * data_train.shape[3] # 3*32*32
shape = (first_dim, second_dim) # (50000, 3072)
# compute the covariance matrix
cov = np.dot(data_train.reshape(shape).T, data_train.reshape(shape)) / data_train.shape[0]
# compute the SVD factorization of the data covariance matrix
U,S,V = np.linalg.svd(cov)
print 'cov.shape = ',cov.shape
print U.shape, S.shape, V.shape
Xrot = np.dot(data_train.reshape(shape), U) # decorrelate the data
Xwhite = Xrot / np.sqrt(S + 1e-5)
print Xwhite.shape
data_whitened = Xwhite.reshape(-1,32,32,3)
print data_whitened.shape
выходы:
cov.shape = (3072L, 3072L)
(3072L, 3072L) (3072L,) (3072L, 3072L)
(50000L, 3072L)
(50000L, 32L, 32L, 3L)
(32L, 32L, 3L)
и пытаемся показать полученное изображение:
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.misc import imshow
print data_whitened[0].shape
fig = plt.figure()
plt.subplot(221)
plt.imshow(data_whitened[0])
plt.subplot(222)
plt.imshow(data_whitened[100])
plt.show()
Кстати data_train[0].shape является (3,32,32), но если я изменить форму побеленного изображения в соответствии с этим я получаю
TypeError: Invalid dimensions for image data
Может ли это быть проблемой визуализации? если так, как я могу убедиться в этом?
Обновить:
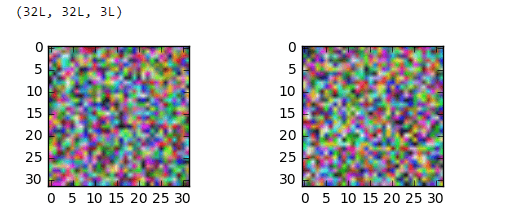
Благодаря @AndrasDeak я исправил код визуализации таким образом, но результат все равно выглядит случайным:
data_whitened = Xwhite.reshape(-1,3,32,32).transpose(0,2,3,1)
print data_whitened.shape
fig = plt.figure()
plt.subplot(221)
plt.imshow(data_whitened[0])
Обновление 2:
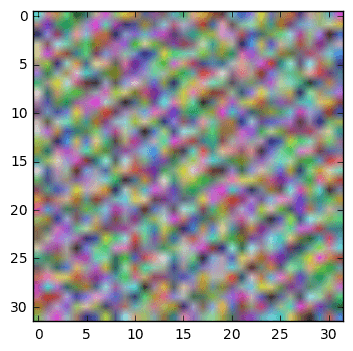
Это то, что я получаю, когда запускаю некоторые из приведенных ниже команд: Как видно из рисунка ниже, toimage может показать изображение очень хорошо, но попытка изменить его форму испортило изображение. 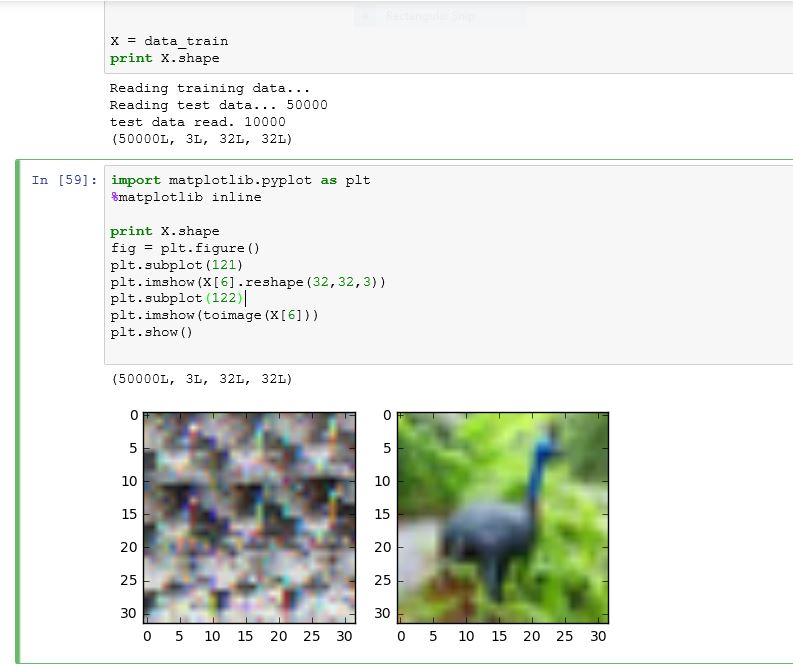
# output is of shape (N, 3, 32, 32)
X = X.reshape((-1,3,32,32))
# output is of shape (N, 32, 32, 3)
X = X.transpose(0,2,3,1)
# put data back into a design matrix (N, 3072)
X = X.reshape(-1, 3072)
plt.imshow(X[6].reshape(32,32,3))
plt.show()
по какой-то странной причине, это было то, что я сначала получил, но затем, после нескольких попыток, он изменился на предыдущее изображение. 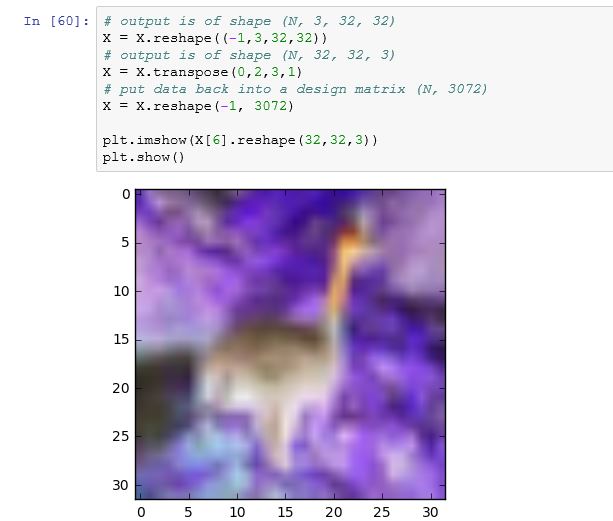
3 ответа
Давайте пройдемся по этому. Как вы указали, CIFAR содержит изображения, которые хранятся в матрице; каждое изображение представляет собой строку, и каждая строка имеет 3072 столбцов uint8 цифры (0-255). Изображения имеют размер 32x32 пикселя, а пиксели - RGB (трехканальный цвет).
# https://www.cs.toronto.edu/~kriz/cifar.html
# wget https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
# tar xf cifar-10-python.tar.gz
import numpy as np
import cPickle
with open('cifar-10-batches-py/data_batch_1') as input_file:
X = cPickle.load(input_file)
X = X['data'] # shape is (N, 3072)
Оказывается, столбцы упорядочены немного забавно: сначала идут все значения красного пикселя, затем все зеленые пиксели, затем все синие пиксели. Это усложняет просмотр изображений. Это:
import matplotlib.pyplot as plt
plt.imshow(X[6].reshape(32,32,3))
plt.show()
дает это:
Итак, просто для удобства просмотра, давайте перемешаем размеры нашей матрицы вокруг reshape а также transpose:
# output is of shape (N, 3, 32, 32)
X = X.reshape((-1,3,32,32))
# output is of shape (N, 32, 32, 3)
X = X.transpose(0,2,3,1)
# put data back into a design matrix (N, 3072)
X = X.reshape(-1, 3072)
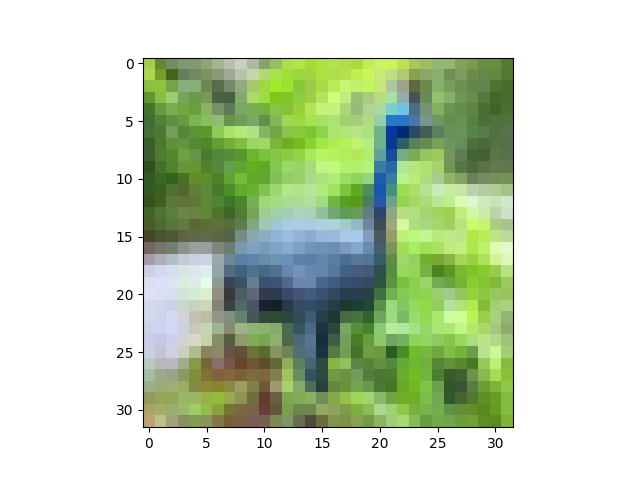
Сейчас:
plt.imshow(X[6].reshape(32,32,3))
plt.show()
дает:
Хорошо, на отбеливание ZCA. Нам часто напоминают, что очень важно центрировать данные до их отбеливания. На данный момент, наблюдение о коде, который вы включаете. Из того, что я могу сказать, компьютерное зрение рассматривает цветовые каналы как еще одно измерение характеристик; нет ничего особенного в отдельных значениях RGB в изображении, как нет ничего особенного в отдельных значениях пикселей. Все они просто числовые функции. Итак, в то время как вы вычисляете среднее значение пикселя, учитывая цветовые каналы (т. Е. Ваш mean это кортеж r,g,b значения), мы просто вычислим среднее значение изображения. Обратите внимание, что X большая матрица с N строками и 3072 столбцами. Мы будем рассматривать каждый столбец как "вещь такого же типа", как и любой другой столбец.
# zero-centre the data (this calculates the mean separately across
# pixels and colour channels)
X = X - X.mean(axis=0)
На этом этапе давайте также проведем глобальную нормализацию контраста, которая довольно часто применяется к данным изображения. Я буду использовать норму L2, которая дает каждому изображению векторную величину 1:
X = X / np.sqrt((X ** 2).sum(axis=1))[:,None]
Можно легко использовать что-то еще, например, стандартное отклонение (X = X / np.std(X, axis=0)) или минимальное-максимальное масштабирование до некоторого интервала, например [-1,1].
Где-то там. На данный момент мы не сильно изменили наши данные, так как мы просто сместили и масштабировали их (линейное преобразование). Чтобы отобразить его, нам нужно вернуть данные изображения в диапазон [0,1], поэтому давайте воспользуемся вспомогательной функцией:
def show(i):
i = i.reshape((32,32,3))
m,M = i.min(), i.max()
plt.imshow((i - m) / (M - m))
plt.show()
show(X[6])
Здесь павлин выглядит немного ярче, но это только потому, что мы растянули его значения в пикселях, чтобы заполнить интервал [0,1]:
ZCA отбеливание:
# compute the covariance of the image data
cov = np.cov(X, rowvar=True) # cov is (N, N)
# singular value decomposition
U,S,V = np.linalg.svd(cov) # U is (N, N), S is (N,)
# build the ZCA matrix
epsilon = 1e-5
zca_matrix = np.dot(U, np.dot(np.diag(1.0/np.sqrt(S + epsilon)), U.T))
# transform the image data zca_matrix is (N,N)
zca = np.dot(zca_matrix, X) # zca is (N, 3072)
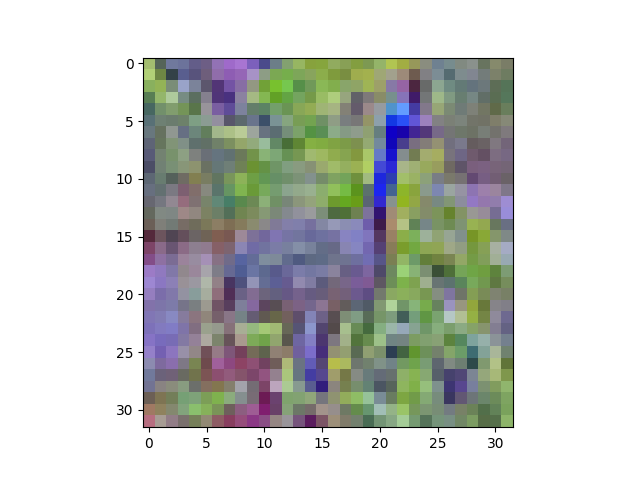
Смотрю (show(zca[6])):
Теперь павлин определенно выглядит иначе. Вы можете видеть, что ZCA повернул изображение в цветовом пространстве, поэтому оно выглядит как изображение на старом телевизоре с отключенным тоном. Тем не менее, узнаваемый.
Предположительно из-за epsilon Значение, которое я использовал, ковариация моих преобразованных данных не совсем идентична, но она довольно близка:
>>> (np.cov(zca, rowvar=True).argmax(axis=1) == np.arange(zca.shape[0])).all()
True
Обновление 29 января
Я не совсем уверен, как решить проблемы, которые у вас возникли; похоже, ваша проблема в настоящее время находится в форме ваших необработанных данных, поэтому я бы посоветовал вам сначала разобраться с этим, прежде чем пытаться перейти к центрированию нуля и ZCA.
С одной стороны, первый график из четырех графиков в вашем обновлении выглядит хорошо, предполагая, что вы правильно загрузили данные CIFAR. Второй сюжет производится toimageЯ думаю, что это автоматически определит, какое измерение имеет данные о цвете, что является хорошим трюком. С другой стороны, то, что идет после этого, выглядит странно, поэтому кажется, что-то где-то идет не так. Признаюсь, я не совсем могу следить за состоянием вашего скрипта, потому что подозреваю, что вы работаете в интерактивном режиме (записная книжка), повторяете вещи, когда они не работают (подробнее об этом через секунду), и что вы используете код что вы не показали в своем вопросе. В частности, я не уверен, как вы загружаете данные CIFAR; ваш скриншот показывает вывод некоторых print заявления (Reading training data...и т. д.), а затем при копировании train_data в X и распечатать shape из Xформа уже преобразована в (N, 3, 32, 32), Как я уже сказал, график обновления 1 будет означать, что изменение формы произошло правильно. Из графиков 3 и 4 я думаю, что вы где-то путаетесь с размерами матрицы, поэтому я не уверен, как вы делаете изменение формы и транспонирование.
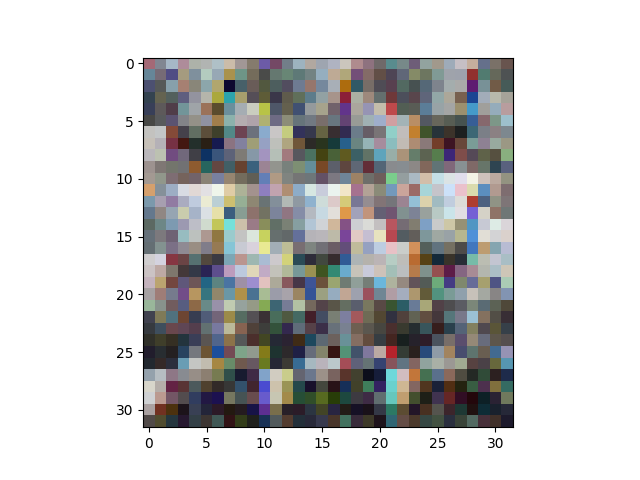
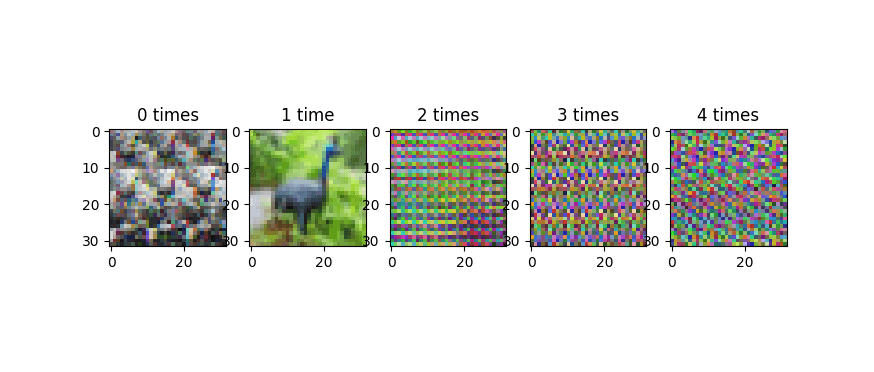
Обратите внимание, что важно быть осторожным с изменением формы и транспонированием по следующей причине. X = X.reshape(...) а также X = X.transpose(...) Код модифицирует матрицу на месте. Если вы сделаете это несколько раз (например, случайно в блокноте jupyter), вы будете перетасовывать оси вашей матрицы снова и снова, и построение графика данных будет выглядеть действительно странно. Это изображение показывает прогресс, когда мы повторяем операции изменения формы и транспонирования:
Эта прогрессия не повторяется, или, по крайней мере, она не повторяется быстро. Из-за периодических закономерностей в данных (например, 32-пиксельная структура строк изображений), вы склонны к полосатости в этих неправильно измененных изображениях. Мне интересно, происходит ли это на третьем из четырех ваших графиков в вашем обновлении, которое выглядит гораздо менее случайным, чем изображения в исходной версии вашего вопроса.
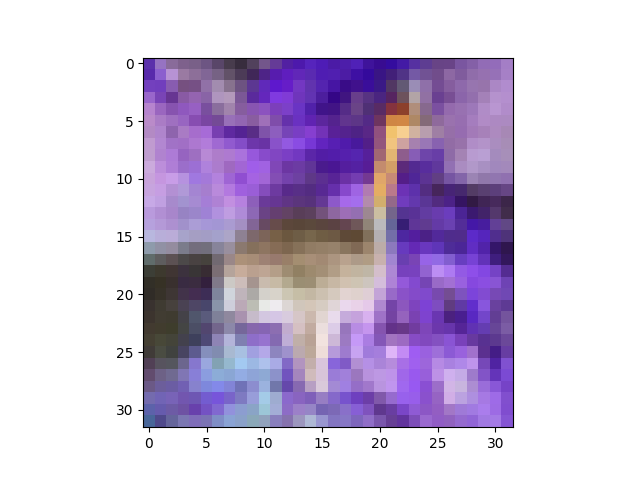
Четвертый сюжет вашего обновления - цветной негатив павлина. Я не уверен, как вы получаете это, но я могу воспроизвести ваш вывод с помощью:
plt.imshow(255 - X[6].reshape(32,32,3))
plt.show()
который дает:
Один из способов получить это, если вы используете мой show вспомогательная функция, и вы перепутали m а также M, как это:
def show(i):
i = i.reshape((32,32,3))
m,M = i.min(), i.max()
plt.imshow((i - M) / (m - M)) # this will produce a negative img
plt.show()
У меня была та же проблема: результирующие прогнозируемые значения выключены:
Предполагается, что плавающее изображение должно иметь значения [0-1,0] для каждого
def toimage(data):
min_ = np.min(data)
max_ = np.max(data)
return (data-min_)/(max_ - min_)
ВНИМАНИЕ: используйте эту функцию только для визуализации!
Однако обратите внимание, как вычисляется матрица "декорреляции" или "отбеливания" @wildwilhelm
zca_matrix = np.dot(U, np.dot(np.diag(1.0/np.sqrt(S + epsilon)), U.T))
Это потому, что U-матрица собственных векторов корреляционной матрицы на самом деле такая: SVD(X) = U,S,V, но U - это собственная база X*X, а не X https://en.wikipedia.org/wiki/Singular-value_decomposition
В заключение, я бы предпочел рассматривать статистические единицы только пиксели, а каналы RGB - их модальности, а не изображения как статистические единицы, а пиксели - модальности. Я пробовал это в базе данных CIFAR 10, и она работает довольно хорошо.
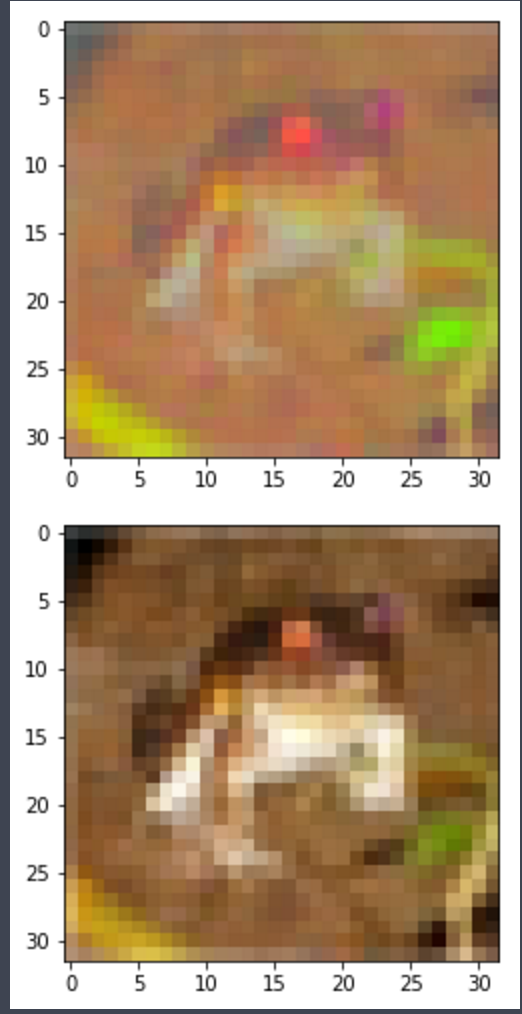
ПРИМЕР ИЗОБРАЖЕНИЯ: верхнее изображение имеет значения RGB, "засохшие", нижнее - оригинал
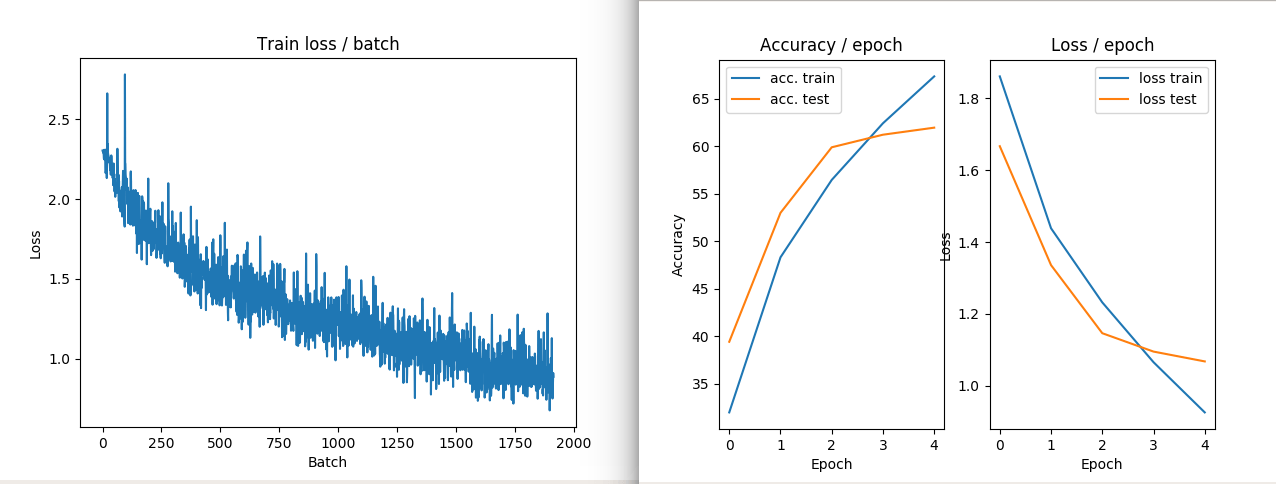
ПРИМЕР ИЗОБРАЖЕНИЯ 2: НЕТ преобразований ZCA в поезде и потере
ПРИМЕР ИЗОБРАЖЕНИЯ 3: трансформация ZCA в поезде и проигрыш
Если вы хотите линейно масштабировать изображение, чтобы оно имело нулевую среднюю и единичную норму, вы можете сделать такое же отбеливание изображения, как и в Tensofrlow. tf.image.per_image_standardization
, После документации необходимо использовать следующую формулу для нормализации каждого изображения независимо:
(image - image_mean) / max(image_stddev, 1.0/sqrt(image_num_elements))
Имейте в виду, что mean и standard deviation должны быть рассчитаны по всем значениям в изображении. Это означает, что нам не нужно указывать оси / оси, вдоль которых они вычисляются.
Способ реализовать это без Tensorflow с помощью numpy следующим образом:
import math
import numpy as np
from PIL import Image
# open image
image = Image.open("your_image.jpg")
image = np.array(image)
# standardize image
mean = image.mean()
stddev = image.std()
adjusted_stddev = max(stddev, 1.0/math.sqrt(image.size))
standardized_image = (image - mean) / adjusted_stddev