Кривая Левенберга Маркварда, подходящая MATLAB
Введите описание изображения здесь, я не знаю, как выбрать lb а также ub за lsqcurvefit в MATLAB, а также x0, чтобы приспособить мою функцию к данным, я имею в виду, что у меня есть вывод, но они не верны
Вот мои данные:
xdata= [22.8700000000000;7.92000000000000;3.45000000000000;1.78000000000000;
1.57000000000000;6.41000000000000;12.9000000000000;1.82000000000000;
1.86000000000000;3.71000000000000;12.0900000000000;15.9900000000000;
18.9600000000000;23.1500000000000;23.4500000000000;24.8200000000000;
25.0700000000000;13.2800000000000];
ydata= [8.44300000000000;7.92100000000000;7.64600000000000;7.51600000000000;
7.47100000000000;7.82100000000000;8.03200000000000;7.76200000000000;
7.77400000000000;7.87800000000000;8.07000000000000;8.26000000000000;
8.40000000000000;8.52000000000000;8.52000000000000;8.57000000000000;
8.58000000000000;8.03200000000000];
и тогда у меня будет myfunc в отдельном файле m:
function F = myfun(x,xdata)
F=x(1)*(1-x(2)^2)./((1+x(2)^2+2*x(2)*cosd(xdata)).^1.5);
я имею x(1) а также x(2)неизвестный, который я хотел бы оценить после подгонки к моим данным, и я знаю, что к x(2) не будет отрицательным значением.
Итак, я установил lsqcurvefit как это:
[x, resnorm]=lsqcurvefit(@myfun,[-0.5:0.5], xdata, ydata, 0, 1.5, options)
И вот результат:
х = 1,5000 -0,4945
resnorm = 52,1739
который показывает отрицательное значение для x(2)!
не могли бы вы мне помочь?
Большое спасибо за ответ на мой вопрос, и теперь, когда команда вычислила x и resnorm, я использую результаты в своей функции, это означает, что я использовал x(1)=92.8054 x(2)=0.7427
так;
F = 92,8054*(1-(0,7427)^2)./((1-0.7427)^2+2*(0,7427)*cosd(XData)) ^1,5.
теперь у меня есть вектор F, когда я строю свои данные и результаты, заговор (xdata, ydata, 'o', xdata, F, '*')
Я не знаю, почему диапазон оси y такой разный! возможно мне нужно добавить х (3) к моей функции.
Я прикрепил рисунок.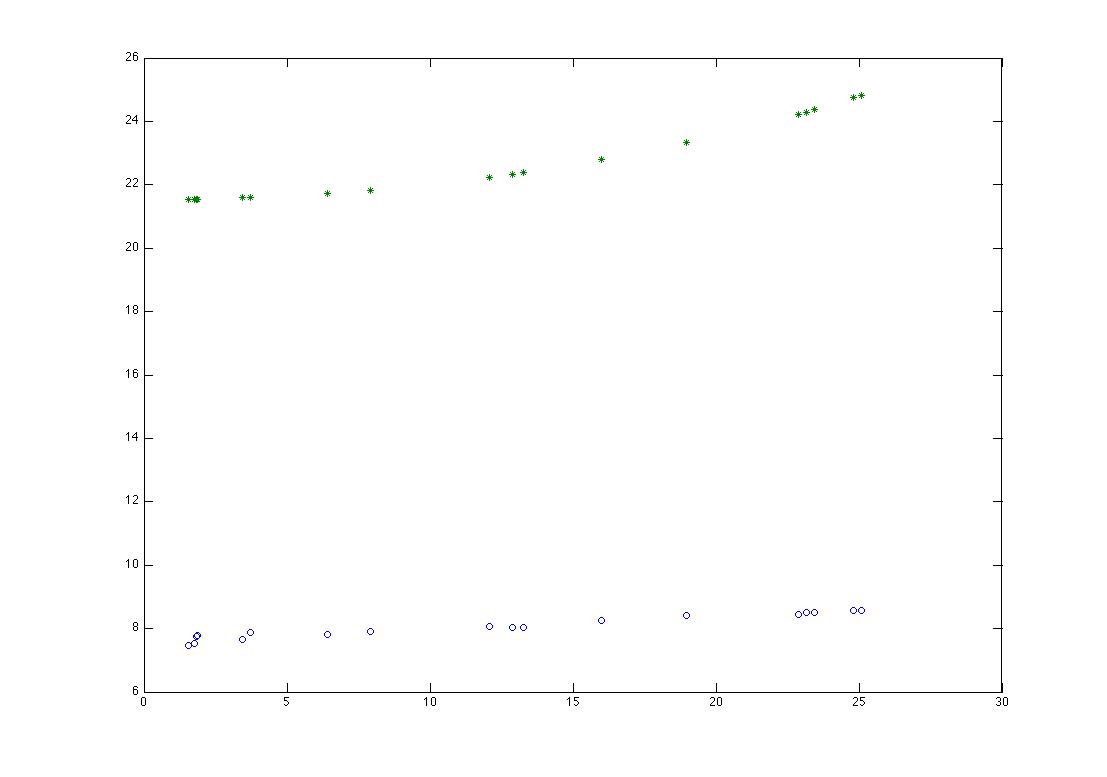
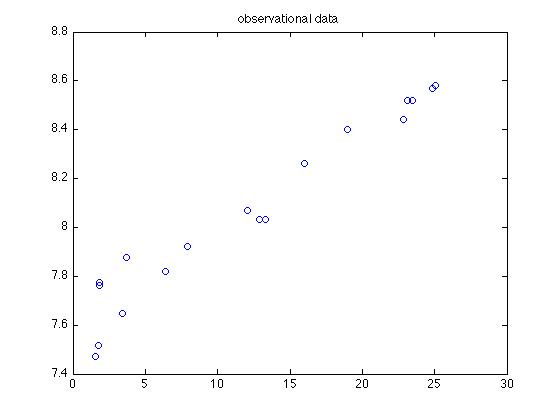
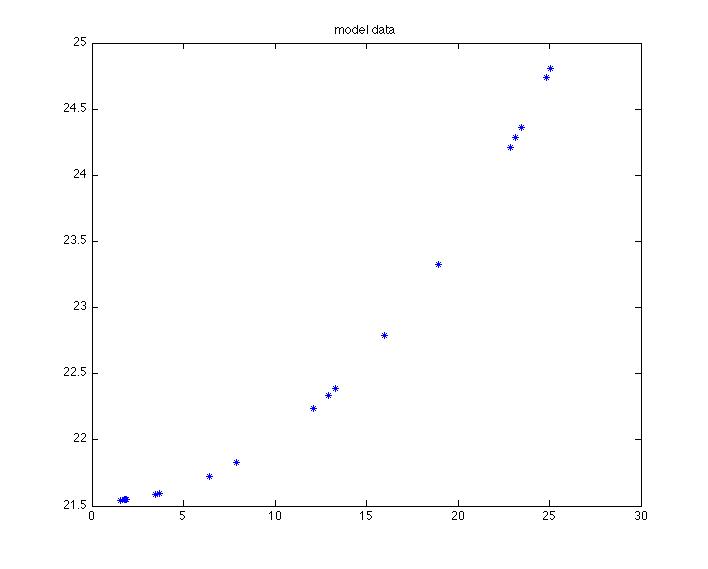
3 ответа
Ваша верхняя и нижняя границы должны быть векторами с тем же числом элементов, что и то, что вы пытаетесь оценить, в вашем случае x.
Так, например, если вы хотите, чтобы x(1) был неограниченным, а x(2) - между 0 и 1,5, попробуйте
[x, resnorm]=lsqcurvefit(@myfun,[-0.5:0.5], xdata, ydata, [-inf, 0], [inf, 1.5], options)
Для расчета F используйте вашу целевую функцию, которую вы уже создали:
F = myfun(x, xdata) и затем подготовьте сюжет так, как вы уже это сделали. В вашем комментарии ниже у вас есть переключатель + к - Вот почему ваши графики не выравниваются.
Параметры lb а также ub нижняя и верхняя границы вашего вывода, т.е. ваше оптимизированное значение xopt удовлетворит lb <= xopt <= ub,
Как вы уже знаете, что x(2) не может быть отрицательным, у вас уже есть одна нижняя граница, которая равна нулю, т.е. lb(2) = 0, Теперь вам нужно только определить нижнюю границу для x(1) и верхние границы для обоих x(1) а также x(2),
Следующий код будет ограничивать x(1) to [-inf, 1e3] а также x(2) to [0, 1e3]:
lb = [-inf, 0];
ub = [1e3, 1e3];
[x, resnorm] = lsqcurvefit(@myfun,[-0.5:0.5], xdata, ydata, 0, 1.5, ...
lb, ub, options)
Я также немного озадачен тем, что ваш подход сработал. Согласно документации, вы должны передавать пустые векторы, если у вас нет верхних или нижних границ, но вы хотите предоставить optionsт.е. твой пример должен читать
[x, resnorm] = lsqcurvefit(@myfun,[-0.5:0.5], xdata, ydata, 0, 1.5, ...
[], [], options)
Возможно, у нас есть разные версии Matlab.
Почему бы не использовать простое решение наименьших квадратов:
in = [ones(size(xdata, 1), 1), xdata];
w = in \ ydata;
ydata_fit = in * w;
Результат:
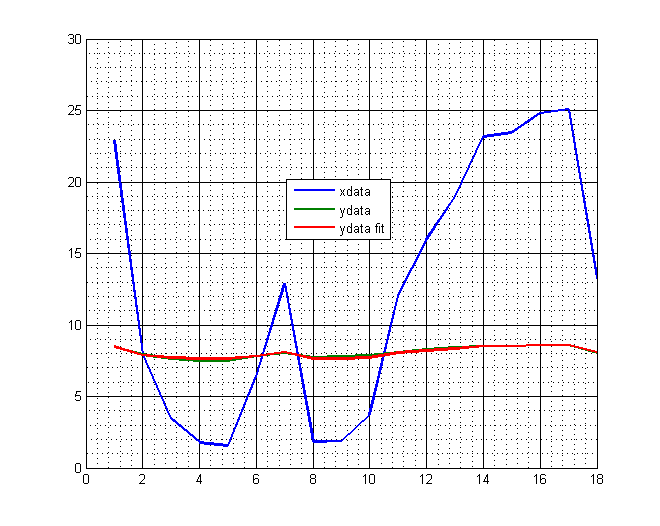
>> disp(w)
7.5744
0.0401