Положение солнца с учетом времени суток, широты и долготы
Этот вопрос был задан чуть более трех лет назад. Был дан ответ, однако я нашел ошибку в решении.
Код ниже написан на R. Я перенес его на другой язык, однако я проверил исходный код непосредственно на R, чтобы убедиться, что проблема не с моим портированием.
sunPosition <- function(year, month, day, hour=12, min=0, sec=0,
lat=46.5, long=6.5) {
twopi <- 2 * pi
deg2rad <- pi / 180
# Get day of the year, e.g. Feb 1 = 32, Mar 1 = 61 on leap years
month.days <- c(0,31,28,31,30,31,30,31,31,30,31,30)
day <- day + cumsum(month.days)[month]
leapdays <- year %% 4 == 0 & (year %% 400 == 0 | year %% 100 != 0) & day >= 60
day[leapdays] <- day[leapdays] + 1
# Get Julian date - 2400000
hour <- hour + min / 60 + sec / 3600 # hour plus fraction
delta <- year - 1949
leap <- trunc(delta / 4) # former leapyears
jd <- 32916.5 + delta * 365 + leap + day + hour / 24
# The input to the Atronomer's almanach is the difference between
# the Julian date and JD 2451545.0 (noon, 1 January 2000)
time <- jd - 51545.
# Ecliptic coordinates
# Mean longitude
mnlong <- 280.460 + .9856474 * time
mnlong <- mnlong %% 360
mnlong[mnlong < 0] <- mnlong[mnlong < 0] + 360
# Mean anomaly
mnanom <- 357.528 + .9856003 * time
mnanom <- mnanom %% 360
mnanom[mnanom < 0] <- mnanom[mnanom < 0] + 360
mnanom <- mnanom * deg2rad
# Ecliptic longitude and obliquity of ecliptic
eclong <- mnlong + 1.915 * sin(mnanom) + 0.020 * sin(2 * mnanom)
eclong <- eclong %% 360
eclong[eclong < 0] <- eclong[eclong < 0] + 360
oblqec <- 23.429 - 0.0000004 * time
eclong <- eclong * deg2rad
oblqec <- oblqec * deg2rad
# Celestial coordinates
# Right ascension and declination
num <- cos(oblqec) * sin(eclong)
den <- cos(eclong)
ra <- atan(num / den)
ra[den < 0] <- ra[den < 0] + pi
ra[den >= 0 & num < 0] <- ra[den >= 0 & num < 0] + twopi
dec <- asin(sin(oblqec) * sin(eclong))
# Local coordinates
# Greenwich mean sidereal time
gmst <- 6.697375 + .0657098242 * time + hour
gmst <- gmst %% 24
gmst[gmst < 0] <- gmst[gmst < 0] + 24.
# Local mean sidereal time
lmst <- gmst + long / 15.
lmst <- lmst %% 24.
lmst[lmst < 0] <- lmst[lmst < 0] + 24.
lmst <- lmst * 15. * deg2rad
# Hour angle
ha <- lmst - ra
ha[ha < -pi] <- ha[ha < -pi] + twopi
ha[ha > pi] <- ha[ha > pi] - twopi
# Latitude to radians
lat <- lat * deg2rad
# Azimuth and elevation
el <- asin(sin(dec) * sin(lat) + cos(dec) * cos(lat) * cos(ha))
az <- asin(-cos(dec) * sin(ha) / cos(el))
elc <- asin(sin(dec) / sin(lat))
az[el >= elc] <- pi - az[el >= elc]
az[el <= elc & ha > 0] <- az[el <= elc & ha > 0] + twopi
el <- el / deg2rad
az <- az / deg2rad
lat <- lat / deg2rad
return(list(elevation=el, azimuth=az))
}
Проблема, которую я поражаю, состоит в том, что азимут, который это возвращает, кажется неправильным. Например, если я запускаю функцию в (южное) летнее солнцестояние в 12:00 для мест 0ºE и 41ºS, 3ºS, 3ºN и 41ºN:
> sunPosition(2012,12,22,12,0,0,-41,0)
$elevation
[1] 72.42113
$azimuth
[1] 180.9211
> sunPosition(2012,12,22,12,0,0,-3,0)
$elevation
[1] 69.57493
$azimuth
[1] -0.79713
Warning message:
In asin(sin(dec)/sin(lat)) : NaNs produced
> sunPosition(2012,12,22,12,0,0,3,0)
$elevation
[1] 63.57538
$azimuth
[1] -0.6250971
Warning message:
In asin(sin(dec)/sin(lat)) : NaNs produced
> sunPosition(2012,12,22,12,0,0,41,0)
$elevation
[1] 25.57642
$azimuth
[1] 180.3084
Эти цифры просто не кажутся правильными. Возвышение, которым я доволен - первые два должны быть примерно одинаковыми, третье - чуть ниже, а четвертое - намного ниже. Однако первый азимут должен быть примерно на север, тогда как число, которое он дает, является полной противоположностью. Остальные три должны указывать примерно на юг, однако только последний делает. Два в средней точке рядом с севером, снова на 180º.
Как вы можете видеть, есть также несколько ошибок, вызванных низкими широтами (закройте экватор)
Я полагаю, что ошибка в этом разделе, с ошибкой, вызванной в третьей строке (начиная с elc).
# Azimuth and elevation
el <- asin(sin(dec) * sin(lat) + cos(dec) * cos(lat) * cos(ha))
az <- asin(-cos(dec) * sin(ha) / cos(el))
elc <- asin(sin(dec) / sin(lat))
az[el >= elc] <- pi - az[el >= elc]
az[el <= elc & ha > 0] <- az[el <= elc & ha > 0] + twopi
Я гуглил и нашел похожий кусок кода в C, преобразовал в R строку, которую он использует для вычисления азимута, что-то вроде
az <- atan(sin(ha) / (cos(ha) * sin(lat) - tan(dec) * cos(lat)))
Вывод здесь, кажется, идет в правильном направлении, но я просто не могу получить его, чтобы дать мне правильный ответ все время, когда он переводится обратно в градусы.
Исправление кода (подозреваю, что это всего лишь несколько строк выше), чтобы заставить его вычислять правильный азимут, было бы фантастическим.
6 ответов
Это кажется важной темой, поэтому я разместил более длинный, чем обычно, ответ: если этот алгоритм будет использоваться другими в будущем, я думаю, важно, чтобы он сопровождался ссылками на литературу, из которой он был получен,
Краткий ответ
Как вы уже заметили, ваш опубликованный код не работает должным образом для мест вблизи экватора или в южном полушарии.
Чтобы это исправить, просто замените эти строки в исходном коде:
elc <- asin(sin(dec) / sin(lat))
az[el >= elc] <- pi - az[el >= elc]
az[el <= elc & ha > 0] <- az[el <= elc & ha > 0] + twopi
с этими:
cosAzPos <- (0 <= sin(dec) - sin(el) * sin(lat))
sinAzNeg <- (sin(az) < 0)
az[cosAzPos & sinAzNeg] <- az[cosAzPos & sinAzNeg] + twopi
az[!cosAzPos] <- pi - az[!cosAzPos]
Теперь он должен работать в любой точке земного шара.
обсуждение
Код в вашем примере адаптирован почти дословно из статьи 1988 года JJ Michalsky (Solar Energy. 40:227-235). Эта статья, в свою очередь, усовершенствовала алгоритм, представленный в статье Р. Уолравена в 1978 году (Solar Energy. 20:393-397). Уолравен сообщил, что метод успешно использовался в течение нескольких лет для точного позиционирования поляризационного радиометра в Дэвисе, Калифорния (38° 33' 14"с.ш., 121° 44' 17" з.д.).
Код Михальского и Вальравена содержит важные / фатальные ошибки. В частности, хотя алгоритм Михальского прекрасно работает в большинстве Соединенных Штатов, он выходит из строя (как вы уже нашли) для областей вблизи экватора или в южном полушарии. В 1989 году Дж. В. Спенсер из Виктории, Австралия, отметил то же самое (Solar Energy. 42(4):353):
Уважаемый господин:
Метод Михальского для назначения вычисленного азимута правильному квадранту, полученному из Уолравена, не дает правильных значений при применении для южных (отрицательных) широт. Кроме того, расчет критической высоты (elc) потерпит неудачу на нулевой широте из-за деления на ноль. Оба эти возражения можно избежать, просто назначив азимут правильному квадранту, учитывая знак cos (азимут).
Мои изменения в вашем коде основаны на исправлениях, предложенных Спенсером в опубликованном комментарии. Я просто несколько изменил их, чтобы убедиться, что функция R sunPosition() остается "векторизованным" (т.е. работает должным образом над векторами местоположений точек, вместо того, чтобы проходить по одной точке за раз).
Точность функции sunPosition()
Чтобы проверить это sunPosition() работает правильно, я сравнил его результаты с результатами, рассчитанными солнечным калькулятором Национальной администрации океанических и атмосферных исследований. В обоих случаях положения солнца были рассчитаны для полудня (12:00 вечера) в день южного летнего солнцестояния (22 декабря) 2012 года. Все результаты были в пределах 0,02 градуса.
testPts <- data.frame(lat = c(-41,-3,3, 41),
long = c(0, 0, 0, 0))
# Sun's position as returned by the NOAA Solar Calculator,
NOAA <- data.frame(elevNOAA = c(72.44, 69.57, 63.57, 25.6),
azNOAA = c(359.09, 180.79, 180.62, 180.3))
# Sun's position as returned by sunPosition()
sunPos <- sunPosition(year = 2012,
month = 12,
day = 22,
hour = 12,
min = 0,
sec = 0,
lat = testPts$lat,
long = testPts$long)
cbind(testPts, NOAA, sunPos)
# lat long elevNOAA azNOAA elevation azimuth
# 1 -41 0 72.44 359.09 72.43112 359.0787
# 2 -3 0 69.57 180.79 69.56493 180.7965
# 3 3 0 63.57 180.62 63.56539 180.6247
# 4 41 0 25.60 180.30 25.56642 180.3083
Другие ошибки в коде
В опубликованном коде есть как минимум две другие (довольно незначительные) ошибки. Первое приводит к тому, что 29 февраля и 1 марта високосных лет считаются 61-м днем года. Вторая ошибка происходит из-за опечатки в оригинальной статье, которая была исправлена Михальским в заметке 1989 года (Solar Energy. 43(5):323).
Этот блок кода показывает ошибочные строки, закомментированные и сопровождаемые исправленными версиями:
# leapdays <- year %% 4 == 0 & (year %% 400 == 0 | year %% 100 != 0) & day >= 60
leapdays <- year %% 4 == 0 & (year %% 400 == 0 | year %% 100 != 0) &
day >= 60 & !(month==2 & day==60)
# oblqec <- 23.429 - 0.0000004 * time
oblqec <- 23.439 - 0.0000004 * time
Исправленная версия sunPosition()
Вот исправленный код, который был проверен выше:
sunPosition <- function(year, month, day, hour=12, min=0, sec=0,
lat=46.5, long=6.5) {
twopi <- 2 * pi
deg2rad <- pi / 180
# Get day of the year, e.g. Feb 1 = 32, Mar 1 = 61 on leap years
month.days <- c(0,31,28,31,30,31,30,31,31,30,31,30)
day <- day + cumsum(month.days)[month]
leapdays <- year %% 4 == 0 & (year %% 400 == 0 | year %% 100 != 0) &
day >= 60 & !(month==2 & day==60)
day[leapdays] <- day[leapdays] + 1
# Get Julian date - 2400000
hour <- hour + min / 60 + sec / 3600 # hour plus fraction
delta <- year - 1949
leap <- trunc(delta / 4) # former leapyears
jd <- 32916.5 + delta * 365 + leap + day + hour / 24
# The input to the Atronomer's almanach is the difference between
# the Julian date and JD 2451545.0 (noon, 1 January 2000)
time <- jd - 51545.
# Ecliptic coordinates
# Mean longitude
mnlong <- 280.460 + .9856474 * time
mnlong <- mnlong %% 360
mnlong[mnlong < 0] <- mnlong[mnlong < 0] + 360
# Mean anomaly
mnanom <- 357.528 + .9856003 * time
mnanom <- mnanom %% 360
mnanom[mnanom < 0] <- mnanom[mnanom < 0] + 360
mnanom <- mnanom * deg2rad
# Ecliptic longitude and obliquity of ecliptic
eclong <- mnlong + 1.915 * sin(mnanom) + 0.020 * sin(2 * mnanom)
eclong <- eclong %% 360
eclong[eclong < 0] <- eclong[eclong < 0] + 360
oblqec <- 23.439 - 0.0000004 * time
eclong <- eclong * deg2rad
oblqec <- oblqec * deg2rad
# Celestial coordinates
# Right ascension and declination
num <- cos(oblqec) * sin(eclong)
den <- cos(eclong)
ra <- atan(num / den)
ra[den < 0] <- ra[den < 0] + pi
ra[den >= 0 & num < 0] <- ra[den >= 0 & num < 0] + twopi
dec <- asin(sin(oblqec) * sin(eclong))
# Local coordinates
# Greenwich mean sidereal time
gmst <- 6.697375 + .0657098242 * time + hour
gmst <- gmst %% 24
gmst[gmst < 0] <- gmst[gmst < 0] + 24.
# Local mean sidereal time
lmst <- gmst + long / 15.
lmst <- lmst %% 24.
lmst[lmst < 0] <- lmst[lmst < 0] + 24.
lmst <- lmst * 15. * deg2rad
# Hour angle
ha <- lmst - ra
ha[ha < -pi] <- ha[ha < -pi] + twopi
ha[ha > pi] <- ha[ha > pi] - twopi
# Latitude to radians
lat <- lat * deg2rad
# Azimuth and elevation
el <- asin(sin(dec) * sin(lat) + cos(dec) * cos(lat) * cos(ha))
az <- asin(-cos(dec) * sin(ha) / cos(el))
# For logic and names, see Spencer, J.W. 1989. Solar Energy. 42(4):353
cosAzPos <- (0 <= sin(dec) - sin(el) * sin(lat))
sinAzNeg <- (sin(az) < 0)
az[cosAzPos & sinAzNeg] <- az[cosAzPos & sinAzNeg] + twopi
az[!cosAzPos] <- pi - az[!cosAzPos]
# if (0 < sin(dec) - sin(el) * sin(lat)) {
# if(sin(az) < 0) az <- az + twopi
# } else {
# az <- pi - az
# }
el <- el / deg2rad
az <- az / deg2rad
lat <- lat / deg2rad
return(list(elevation=el, azimuth=az))
}
Рекомендации:
Михальский, JJ 1988. Алгоритм астрономического альманаха для приближенного положения Солнца (1950-2050). Солнечная энергия. 40(3):227-235.
Михальский, JJ 1989. Ошибки. Солнечная энергия. 43(5):323.
Спенсер, JW 1989. Комментарии к "Алгоритму астрономического альманаха для приблизительного положения Солнца (1950-2050)". Солнечная энергия. 42 (4): 353.
Walraven, R. 1978. Расчет положения солнца. Солнечная энергия. 20:393-397.
Используя "Солнечные вычисления NOAA" по одной из ссылок выше, я немного изменил финальную часть функции, используя немного другой алгоритм, который, я надеюсь, был переведен без ошибок. Я закомментировал бесполезный теперь код и добавил новый алгоритм сразу после преобразования широты в радианы:
# -----------------------------------------------
# New code
# Solar zenith angle
zenithAngle <- acos(sin(lat) * sin(dec) + cos(lat) * cos(dec) * cos(ha))
# Solar azimuth
az <- acos(((sin(lat) * cos(zenithAngle)) - sin(dec)) / (cos(lat) * sin(zenithAngle)))
rm(zenithAngle)
# -----------------------------------------------
# Azimuth and elevation
el <- asin(sin(dec) * sin(lat) + cos(dec) * cos(lat) * cos(ha))
#az <- asin(-cos(dec) * sin(ha) / cos(el))
#elc <- asin(sin(dec) / sin(lat))
#az[el >= elc] <- pi - az[el >= elc]
#az[el <= elc & ha > 0] <- az[el <= elc & ha > 0] + twopi
el <- el / deg2rad
az <- az / deg2rad
lat <- lat / deg2rad
# -----------------------------------------------
# New code
if (ha > 0) az <- az + 180 else az <- 540 - az
az <- az %% 360
# -----------------------------------------------
return(list(elevation=el, azimuth=az))
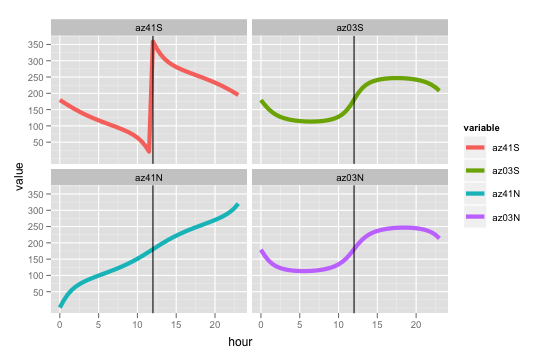
Чтобы проверить азимутальный тренд в четырех упомянутых вами случаях, построим график в зависимости от времени суток:
hour <- seq(from = 0, to = 23, by = 0.5)
azimuth <- data.frame(hour = hour)
az41S <- apply(azimuth, 1, function(x) sunPosition(2012,12,22,x,0,0,-41,0)$azimuth)
az03S <- apply(azimuth, 1, function(x) sunPosition(2012,12,22,x,0,0,-03,0)$azimuth)
az03N <- apply(azimuth, 1, function(x) sunPosition(2012,12,22,x,0,0,03,0)$azimuth)
az41N <- apply(azimuth, 1, function(x) sunPosition(2012,12,22,x,0,0,41,0)$azimuth)
azimuth <- cbind(azimuth, az41S, az03S, az41N, az03N)
rm(az41S, az03S, az41N, az03N)
library(ggplot2)
azimuth.plot <- melt(data = azimuth, id.vars = "hour")
ggplot(aes(x = hour, y = value, color = variable), data = azimuth.plot) +
geom_line(size = 2) +
geom_vline(xintercept = 12) +
facet_wrap(~ variable)
Изображение прикреплено:
Вот переписывание, которое более идиоматично для R, и его легче отлаживать и поддерживать. По сути, это ответ Джоша, но с азимутом, рассчитанным с использованием алгоритмов Джоша и Чарли для сравнения. Я также включил упрощения в код даты из моего другого ответа. Основной принцип состоял в том, чтобы разбить код на множество мелких функций, для которых вам будет проще написать модульные тесты.
astronomersAlmanacTime <- function(x)
{
# Astronomer's almanach time is the number of
# days since (noon, 1 January 2000)
origin <- as.POSIXct("2000-01-01 12:00:00")
as.numeric(difftime(x, origin, units = "days"))
}
hourOfDay <- function(x)
{
x <- as.POSIXlt(x)
with(x, hour + min / 60 + sec / 3600)
}
degreesToRadians <- function(degrees)
{
degrees * pi / 180
}
radiansToDegrees <- function(radians)
{
radians * 180 / pi
}
meanLongitudeDegrees <- function(time)
{
(280.460 + 0.9856474 * time) %% 360
}
meanAnomalyRadians <- function(time)
{
degreesToRadians((357.528 + 0.9856003 * time) %% 360)
}
eclipticLongitudeRadians <- function(mnlong, mnanom)
{
degreesToRadians(
(mnlong + 1.915 * sin(mnanom) + 0.020 * sin(2 * mnanom)) %% 360
)
}
eclipticObliquityRadians <- function(time)
{
degreesToRadians(23.439 - 0.0000004 * time)
}
rightAscensionRadians <- function(oblqec, eclong)
{
num <- cos(oblqec) * sin(eclong)
den <- cos(eclong)
ra <- atan(num / den)
ra[den < 0] <- ra[den < 0] + pi
ra[den >= 0 & num < 0] <- ra[den >= 0 & num < 0] + 2 * pi
ra
}
rightDeclinationRadians <- function(oblqec, eclong)
{
asin(sin(oblqec) * sin(eclong))
}
greenwichMeanSiderealTimeHours <- function(time, hour)
{
(6.697375 + 0.0657098242 * time + hour) %% 24
}
localMeanSiderealTimeRadians <- function(gmst, long)
{
degreesToRadians(15 * ((gmst + long / 15) %% 24))
}
hourAngleRadians <- function(lmst, ra)
{
((lmst - ra + pi) %% (2 * pi)) - pi
}
elevationRadians <- function(lat, dec, ha)
{
asin(sin(dec) * sin(lat) + cos(dec) * cos(lat) * cos(ha))
}
solarAzimuthRadiansJosh <- function(lat, dec, ha, el)
{
az <- asin(-cos(dec) * sin(ha) / cos(el))
cosAzPos <- (0 <= sin(dec) - sin(el) * sin(lat))
sinAzNeg <- (sin(az) < 0)
az[cosAzPos & sinAzNeg] <- az[cosAzPos & sinAzNeg] + 2 * pi
az[!cosAzPos] <- pi - az[!cosAzPos]
az
}
solarAzimuthRadiansCharlie <- function(lat, dec, ha)
{
zenithAngle <- acos(sin(lat) * sin(dec) + cos(lat) * cos(dec) * cos(ha))
az <- acos((sin(lat) * cos(zenithAngle) - sin(dec)) / (cos(lat) * sin(zenithAngle)))
ifelse(ha > 0, az + pi, 3 * pi - az) %% (2 * pi)
}
sunPosition <- function(when = Sys.time(), format, lat = 46.5, long = 6.5)
{
if(is.character(when)) when <- strptime(when, format)
when <- lubridate::with_tz(when, "UTC")
time <- astronomersAlmanacTime(when)
hour <- hourOfDay(when)
# Ecliptic coordinates
mnlong <- meanLongitudeDegrees(time)
mnanom <- meanAnomalyRadians(time)
eclong <- eclipticLongitudeRadians(mnlong, mnanom)
oblqec <- eclipticObliquityRadians(time)
# Celestial coordinates
ra <- rightAscensionRadians(oblqec, eclong)
dec <- rightDeclinationRadians(oblqec, eclong)
# Local coordinates
gmst <- greenwichMeanSiderealTimeHours(time, hour)
lmst <- localMeanSiderealTimeRadians(gmst, long)
# Hour angle
ha <- hourAngleRadians(lmst, ra)
# Latitude to radians
lat <- degreesToRadians(lat)
# Azimuth and elevation
el <- elevationRadians(lat, dec, ha)
azJ <- solarAzimuthRadiansJosh(lat, dec, ha, el)
azC <- solarAzimuthRadiansCharlie(lat, dec, ha)
data.frame(
elevation = radiansToDegrees(el),
azimuthJ = radiansToDegrees(azJ),
azimuthC = radiansToDegrees(azC)
)
}
Это рекомендуемое обновление отличного ответа Джоша.
Большая часть запуска функции - это стандартный код для расчета количества дней с полудня 1 января 2000 года. Это гораздо лучше, если использовать существующую функцию даты и времени R.
Я также думаю, что вместо шести различных переменных для указания даты и времени проще (и более согласованно с другими функциями R) указать существующий объект даты или строки даты + строки формата.
Вот две вспомогательные функции
astronomers_almanac_time <- function(x)
{
origin <- as.POSIXct("2000-01-01 12:00:00")
as.numeric(difftime(x, origin, units = "days"))
}
hour_of_day <- function(x)
{
x <- as.POSIXlt(x)
with(x, hour + min / 60 + sec / 3600)
}
И запуск функции теперь упрощается до
sunPosition <- function(when = Sys.time(), format, lat=46.5, long=6.5) {
twopi <- 2 * pi
deg2rad <- pi / 180
if(is.character(when)) when <- strptime(when, format)
time <- astronomers_almanac_time(when)
hour <- hour_of_day(when)
#...
Другая странность в линиях как
mnlong[mnlong < 0] <- mnlong[mnlong < 0] + 360
поскольку mnlong имел %% Обращаясь к его значениям, они все уже должны быть неотрицательными, так что эта строка лишняя.
Мне нужно было положение солнца в проекте Python. Я адаптировал алгоритм Джоша О'Брайена.
Спасибо, Джош.
На случай, если это кому-нибудь пригодится, вот моя адаптация.
Обратите внимание, что моему проекту требовалось только мгновенное положение солнца, поэтому время не является параметром.
def sunPosition(lat=46.5, long=6.5):
# Latitude [rad]
lat_rad = math.radians(lat)
# Get Julian date - 2400000
day = time.gmtime().tm_yday
hour = time.gmtime().tm_hour + \
time.gmtime().tm_min/60.0 + \
time.gmtime().tm_sec/3600.0
delta = time.gmtime().tm_year - 1949
leap = delta / 4
jd = 32916.5 + delta * 365 + leap + day + hour / 24
# The input to the Atronomer's almanach is the difference between
# the Julian date and JD 2451545.0 (noon, 1 January 2000)
t = jd - 51545
# Ecliptic coordinates
# Mean longitude
mnlong_deg = (280.460 + .9856474 * t) % 360
# Mean anomaly
mnanom_rad = math.radians((357.528 + .9856003 * t) % 360)
# Ecliptic longitude and obliquity of ecliptic
eclong = math.radians((mnlong_deg +
1.915 * math.sin(mnanom_rad) +
0.020 * math.sin(2 * mnanom_rad)
) % 360)
oblqec_rad = math.radians(23.439 - 0.0000004 * t)
# Celestial coordinates
# Right ascension and declination
num = math.cos(oblqec_rad) * math.sin(eclong)
den = math.cos(eclong)
ra_rad = math.atan(num / den)
if den < 0:
ra_rad = ra_rad + math.pi
elif num < 0:
ra_rad = ra_rad + 2 * math.pi
dec_rad = math.asin(math.sin(oblqec_rad) * math.sin(eclong))
# Local coordinates
# Greenwich mean sidereal time
gmst = (6.697375 + .0657098242 * t + hour) % 24
# Local mean sidereal time
lmst = (gmst + long / 15) % 24
lmst_rad = math.radians(15 * lmst)
# Hour angle (rad)
ha_rad = (lmst_rad - ra_rad) % (2 * math.pi)
# Elevation
el_rad = math.asin(
math.sin(dec_rad) * math.sin(lat_rad) + \
math.cos(dec_rad) * math.cos(lat_rad) * math.cos(ha_rad))
# Azimuth
az_rad = math.asin(
- math.cos(dec_rad) * math.sin(ha_rad) / math.cos(el_rad))
if (math.sin(dec_rad) - math.sin(el_rad) * math.sin(lat_rad) < 0):
az_rad = math.pi - az_rad
elif (math.sin(az_rad) < 0):
az_rad += 2 * math.pi
return el_rad, az_rad
Я столкнулся с небольшой проблемой с точкой данных и функциями Ричи Коттона выше (в реализации кода Чарли)
longitude= 176.0433687000000020361767383292317390441894531250
latitude= -39.173830619999996827118593500927090644836425781250
event_time = as.POSIXct("2013-10-24 12:00:00", format="%Y-%m-%d %H:%M:%S", tz = "UTC")
sunPosition(when=event_time, lat = latitude, long = longitude)
elevation azimuthJ azimuthC
1 -38.92275 180 NaN
Warning message:
In acos((sin(lat) * cos(zenithAngle) - sin(dec))/(cos(lat) * sin(zenithAngle))) : NaNs produced
потому что в функции solarAzimuthRadiansCharlie было возбуждение с плавающей запятой вокруг угла 180, так что (sin(lat) * cos(zenithAngle) - sin(dec)) / (cos(lat) * sin(zenithAngle)) самое маленькое количество больше 1, 1.0000000000000004440892098, которое генерирует NaN, так как входные данные для acos не должны быть выше 1 или ниже -1.
Я подозреваю, что могут быть аналогичные крайние случаи для вычисления Джоша, где эффекты округления с плавающей запятой приводят к тому, что вход для шага asin выходит за пределы -1: 1, но я не поразил их в моем конкретном наборе данных.
В полудюжине или около того случаев, которые я затронул, "истина" (середина дня или ночи) - это когда проблема возникает так эмпирически, истинное значение должно быть 1/-1. По этой причине мне было бы удобно исправить это, применив шаг округления внутри solarAzimuthRadiansJosh а также solarAzimuthRadiansCharlie, Я не уверен, какова теоретическая точность алгоритма NOAA (точка, в которой численная точность все равно перестает иметь значение), но округление до 12 десятичных знаков зафиксировало данные в моем наборе данных.