Кривая подгонка или интерполяция на графике полулогии с использованием scipy

Question

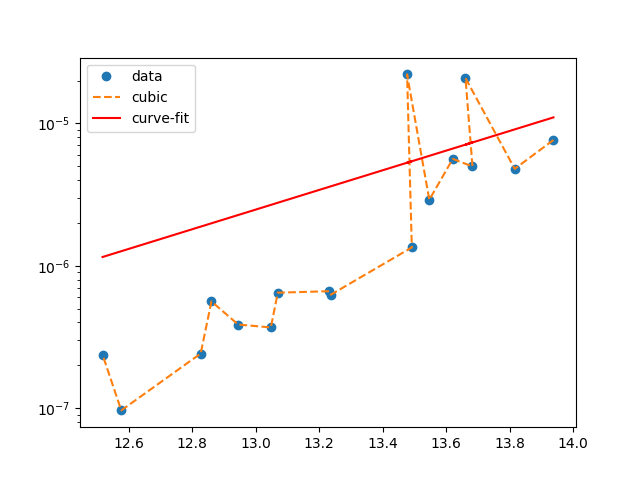
У меня очень мало точек данных, и я хочу создать линию, которая наилучшим образом соответствует точкам данных при построении в полулогическом масштабе. Я пробовал кривую и кубическую интерполяцию от scipy, но ни одна из них не кажется мне очень разумной по сравнению с трендом данных.

Я прошу вас проверить, есть ли более эффективный способ создать прямую линию, подходящую для данных. Вероятно, экстраполяция может сделать, но я не нашел хорошую документацию по экстраполяции на Python.

ваша помощь очень ценится

import sys
import os
import numpy
import matplotlib.pyplot as plt
from pylab import *
from scipy.optimize import curve_fit
import scipy.optimize as optimization
from scipy.interpolate import interp1d
from scipy import interpolate

Mass500 = numpy.array([ 13.938 , 13.816,  13.661,  13.683,  13.621,  13.547,  13.477,  13.492,  13.237,
  13.232,  13.07,   13.048,  12.945,  12.861,  12.827,  12.577,  12.518])

y500 = numpy.array([  7.65103978e-06,   4.79865790e-06,   2.08218909e-05,   4.98385924e-06,
   5.63462673e-06,   2.90785458e-06,   2.21166794e-05,   1.34501705e-06,
   6.26021870e-07,   6.62368879e-07,   6.46735547e-07,   3.68589447e-07,
   3.86209019e-07,   5.61293275e-07,   2.41428755e-07,   9.62491134e-08,
   2.36892162e-07])



plt.semilogy(Mass500, y500, 'o')


# interpolation
f2 = interp1d(Mass500, y500, kind='cubic')
plt.semilogy(Mass500, f2(Mass500), '--')


# curve-fit
def line(x, a, b):
    return 10**(a*x+b)

#Initial guess.
x0     = numpy.array([1.e-6, 1.e-6])

print optimization.curve_fit(line, Mass500, y500, x0)
popt, pcov = curve_fit(line, Mass500, y500)
print popt
plt.semilogy(Mass500, line(Mass500, popt[0], popt[1]), 'r-')



plt.legend(['data', 'cubic', 'curve-fit'], loc='best')

show()

Answer 1

Есть много функций регрессии, доступных в numpy и scipy. scipy.stats.lingress является одной из более простых функций, и она возвращает общие параметры линейной регрессии.

Вот два варианта подгонки полулоговых данных:

1. Трансформированные данные графика
2. Масштабирование осей и преобразование значений функций ввода / вывода

Дано

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt

%matplotlib inline


# Data
mass500 = np.array([ 
    13.938 , 13.816,  13.661,  13.683,
    13.621,  13.547,  13.477,  13.492,
    13.237,  13.232,  13.07,   13.048,  
    12.945,  12.861,  12.827,  12.577,  
    12.518
])

y500 = np.array([  
    7.65103978e-06,   4.79865790e-06,   2.08218909e-05,   4.98385924e-06,
    5.63462673e-06,   2.90785458e-06,   2.21166794e-05,   1.34501705e-06,
    6.26021870e-07,   6.62368879e-07,   6.46735547e-07,   3.68589447e-07,
    3.86209019e-07,   5.61293275e-07,   2.41428755e-07,   9.62491134e-08,
    2.36892162e-07
])

Код

Вариант 1: Трансформированные данные графика

# Regression Function
def regress(x, y):
    """Return a tuple of predicted y values and parameters for linear regression."""
    p = sp.stats.linregress(x, y)
    b1, b0, r, p_val, stderr = p
    y_pred = sp.polyval([b1, b0], x)
    return y_pred, p

# Plotting
x, y = mass500, np.log(y500)                      # transformed data
y_pred, _ = regress(x, y)

plt.plot(x, y, "mo", label="Data")
plt.plot(x, y_pred, "k--", label="Pred.")
plt.xlabel("Mass500")
plt.ylabel("log y500")                            # label axis
plt.legend()

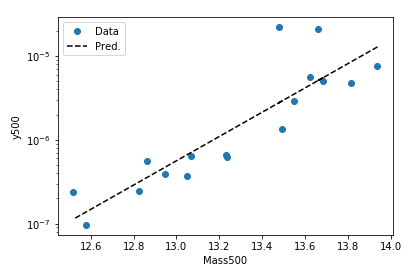
Выход

Простой подход заключается в построении преобразованных данных и маркировке соответствующих логарифмических осей.

---

Вариант 2. Масштабирование осей и преобразование значений функций ввода / вывода

Код

x, y = mass500, y500                              # data, non-transformed
y_pred, _ = regress(x, np.log(y))                 # transformed input             

plt.plot(x, y, "o", label="Data")
plt.plot(x, np.exp(y_pred), "k--", label="Pred.") # transformed output
plt.xlabel("Mass500")
plt.ylabel("y500")
plt.semilogy()
plt.legend()

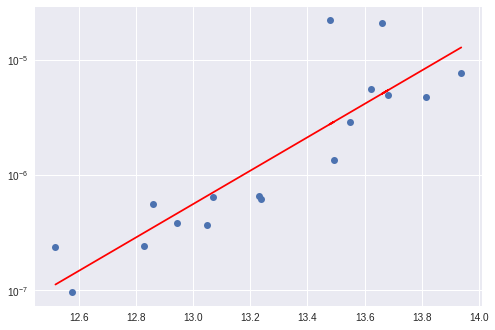
Выход

Второй вариант - изменить оси на полулогарифмическую шкалу (через plt.semilogy()). Здесь нетрансформированные данные естественно выглядят линейными. Также обратите внимание, что метки представляют данные как есть.

Чтобы сделать точную регрессию, остается только преобразовать данные, переданные в функцию регрессии (через np.log(x) или же np.log10(x)), чтобы вернуть правильные параметры регрессии. Это преобразование немедленно отменяется при построении предикатных значений с использованием дополнительной операции, т.е. np.exp(x) или же 10**x,

Answer 2

Если вы хотите, чтобы линия выглядела хорошо в масштабе log-y, то подгоните ее под логарифмы значений y.

def line(x, a, b):
    return a*x+b
popt, pcov = curve_fit(line, Mass500, np.log10(y500))
plt.semilogy(Mass500, 10**line(Mass500, popt[0], popt[1]), 'r-')

Это оно; Я только пропустил кубическую часть интерполяции, которая не казалась актуальной.