Как избежать переобучения в множественной линейной регрессии (lm) в R, поскольку степень полинома увеличивается вместе с статистикой подгонки [закрыто]
Я подгоняю несколько линейных регрессий к набору данных, в котором подобранная плоскость должна аппроксимировать значения, равные 99; красновато-оранжевые точки на рисунке ниже. Я тестирую посадки со степенью полинома от 1 до 7.
Моя проблема в том, что при использовании общих показателей производительности линейной модели, чем выше степень полинома, тем лучше соответствие (очевидно), но это (i) не имеет смысла с научной точки зрения, и (ii) модель (подобранная поверхность) не может быть впоследствии использовался из-за своей формы (местами загибается назад). Для того, чтобы иметь возможность использовать функцию самолета после я должен был бы монотонная гладкая поверхность наклон в заданном направлении , как это: 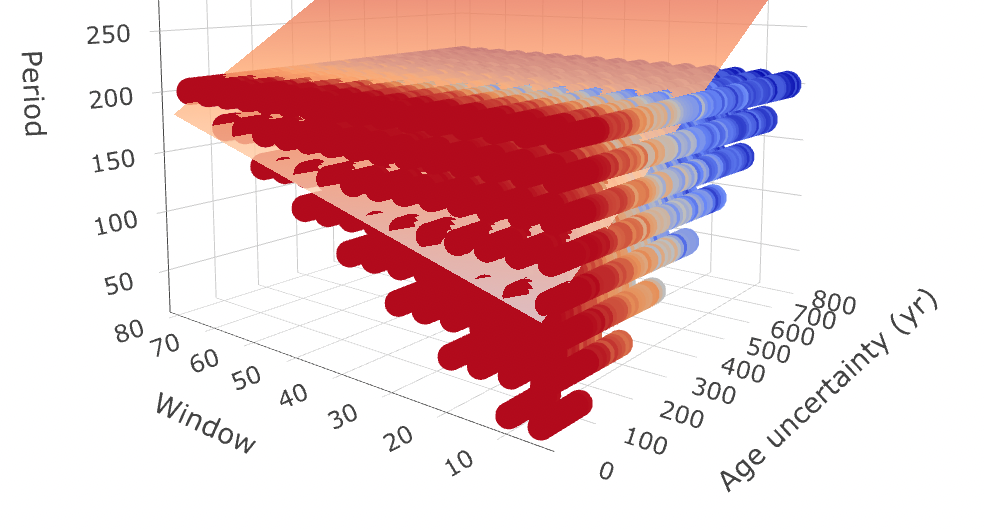 .
.
Модель первой степени обеспечивает именно это, но хуже всего подходит для AIC, BIC, прил. R2 и т. Д.
Данные здесь (mdata_nem_interp2) и использование I - код модели в R это один.
library(performance)
library(stats)
centrum=99
Weight_nem_interp=1/(centrum-mdata_nem_interp2$value)^2
Weight_nem_interp[mapply(is.infinite, Weight_nem_interp)] <- 1
per_lm1 <- lm(variable ~ polym(Unc, Window, degree=1, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm2 <- lm(variable ~ polym(Unc, Window, degree=2, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm3 <- lm(variable ~ polym(Unc, Window, degree=3, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm4 <- lm(variable ~ polym(Unc, Window, degree=4, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm5 <- lm(variable ~ polym(Unc, Window, degree=5, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm6 <- lm(variable ~ polym(Unc, Window, degree=6, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
per_lm7 <- lm(variable ~ polym(Unc, Window, degree=7, raw=TRUE),data = mdata_nem_interp2, weights = Weight_nem_interp)
#Evaluation
#Get the performance metrics
model_performance(per_lm1)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56882.588 | 56907.695 | 0.282 | 0.282 | 76.943 | 18.289
> model_performance(per_lm2)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56824.623 | 56868.562 | 0.293 | 0.293 | 56.366 | 18.147
> model_performance(per_lm3)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56801.164 | 56870.210 | 0.299 | 0.298 | 52.652 | 18.084
> model_performance(per_lm4)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56790.610 | 56891.041 | 0.303 | 0.300 | 45.092 | 18.048
> model_performance(per_lm5)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56786.532 | 56924.623 | 0.306 | 0.302 | 47.961 | 18.025
> model_performance(per_lm6)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56775.245 | 56957.276 | 0.310 | 0.305 | 59.946 | 17.984
> model_performance(per_lm7)
# Indices of model performance
AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
-----------------------------------------------------------
56755.145 | 56987.390 | 0.316 | 0.310 | 62.748 | 17.920
Мои вопросы),
- (i) какие альтернативные метрики я мог бы использовать для оценки производительности моделей с другого аспекта, что дает штраф за переобучение,
- (ii) стоит ли попробовать использовать другую модель?
- (iii) есть ли литература, которую я мог бы использовать, чтобы спорить, почему я должен использовать линейную аппроксимацию?
Спасибо за любые предложения.