Использование квадрата SciPy для получения главного значения интеграла путем интегрирования чуть ниже и чуть выше особой точки

Question

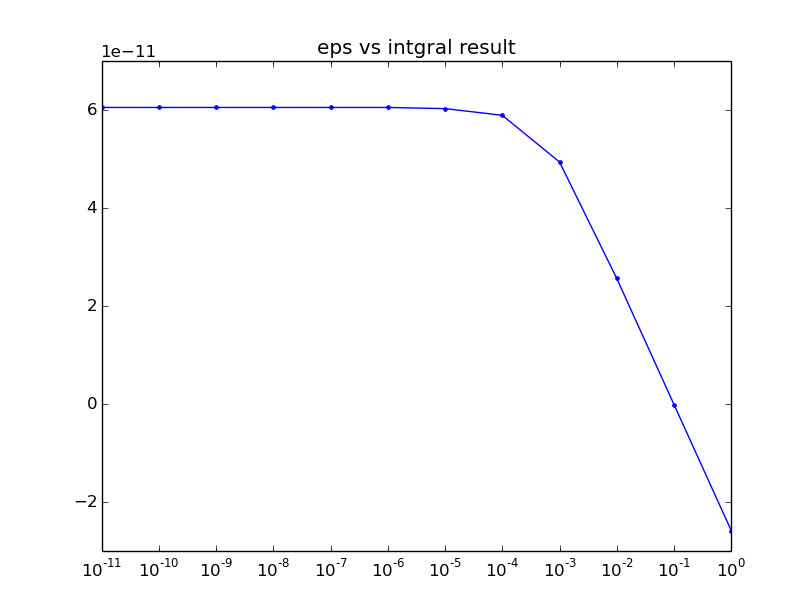
Я пытаюсь вычислить главное значение интеграла (по s) 1/((s - q02)*(s - q2)) на [Ecut, inf] с q02

ln ((q2-Ecut)/(Ecut-q02)) / (q02 -q2)

В приведенном ниже конкретном примере это дает результат -1,58637*10^-11. Нужно также иметь возможность получить тот же результат, разделив интеграл на две части, интегрируя до q2-eps, а затем начиная с q2 + eps, а затем сложив два результата (расхождения должны быть отменены). Принимая EPS все меньше и меньше, нужно восстановить результат выше. Когда я реализую это в scipi, используя quad, мой результат сходится к неправильному результату 6.04685e-11, как я показываю на графике eps против интегрального результата, который я включаю.
Почему квад это делает? даже если у меня есть eps = 0, это дает мне неправильный результат, когда я ожидаю, что он выдаст мне ошибку, когда объект взорвется...

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad


q02  = 485124412.
Ecut = 17909665929.
q2   = 90000000000.

def integrand(s):
    return 1/((s - q02)*(s - q2))

xx=[1.,0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.00000001,
    0.000000001,0.0000000001,0.00000000001,0.]

integral = [0*y for y in xx]
i=0
for eps in xx:

    ans1,err = quad(integrand, Ecut, q2 -eps )
    ans2,err= quad(integrand, q2 + eps, np.inf)

    integral[i] = ans1 + ans2
    i=i+1

plt.semilogx(xx,integral,marker='.')
plt.show()

Answer 1

Нужно также иметь возможность получить тот же результат, разделив интеграл на две части, интегрируя до q2 - eps, а затем начиная с q2 + eps, а затем сложив два результата.

Только если вычисления были совершенно точными. В числовой практике то, что вы описали, по сути является худшей вещью, которую можно сделать. Вы получаете два больших интеграла противоположных знаков, которые почти добавляются друг к другу при добавлении; то, что осталось, больше связано с ошибками интегрирования, чем с фактическим значением интеграла.

Я заметил, что вы проигнорировали значения ошибок err в вашем сценарии, даже не распечатывая их. Плохая идея: они имеют размер 1e-10, что уже скажет вам, что конечный результат с "что-то e-11" является мусором.

Вопрос вычислительной науки Числовая интеграция основных значений - Гильберт как будто решает эту проблему. Один из подходов, которые они указывают, состоит в том, чтобы добавить значения подынтегрального выражения в точках, симметричных относительно особенности, прежде чем пытаться интегрировать ее. Для этого требуется взять интеграл по симметричному интервалу с центром в сингулярности q2 (то есть от Ecut до 2*q2-Ecut), а затем добавить вклад интеграла от 2 * q2-Ecut до бесконечности. Этот раскол в любом случае имеет смысл, потому что quad трактует бесконечные пределы совсем по-другому (используя интеграцию Фурье), что является еще одной вещью, которая будет влиять на то, как сингулярность компенсируется.

Таким образом, реализация этого подхода будет

ans1, err = quad(lambda s: integrand(s) + integrand(2*q2-s), Ecut, q2)
ans2, err = quad(integrand, 2*q2-Ecut, np.inf)

EPS не требуется. Тем не менее, результат все еще выключен: это о -2.5e-11, Оказывается, второй интеграл является виновником. К сожалению, интегральный подход Фурье здесь не кажется эффективным (или я не нашел способа заставить его работать). Оказывается, что предоставление большого, но конечного значения в качестве верхнего предела приводит к лучшему результату, особенно если опция epsabs также используется, например, epsabs=1e-20,

А еще лучше, внимательно прочитайте документацию по quad и обратите внимание, что он напрямую поддерживает интегралы с весом Коши 1/(s-q2), выбирая для них подходящий числовой метод. Это все еще требует конечного верхнего предела и небольшого значения epsabs, но результат довольно точный:

quad(lambda s: 1/(s - q02), Ecut, 1e9*q2, weight='cauchy', wvar=q2, epsabs=1e-20)

возвращается -1.5863735715967363e-11по сравнению с точным значением -1.5863735704856253e-11, Обратите внимание, что коэффициент 1 / (s-q2) не отображается в подынтегральном выражении выше, поскольку он относится к весовым опциям.