Определить, пересекаются ли две линии

Question

Я видел много сообщений здесь на stackru, которые обсуждают эту тему. Я принял решение от stackru, но не смог найти публикацию. Было сказано: если две линии пересекаются, то перекрестный продукт дает для левой и правой стороны два разных результата. Один положительный и один отрицательный. В противном случае оба имеют одинаковый знак. Пока все в порядке. Используется формула, где AB - одна строка, а CD - другая.

dotproductleft = (Bx-Axe)(Cy-By)-(By-Ay)(Cx-Bx)

dotproductright = (Bx-Axe)(Dy-By)-(By-Ay)(Dx-Bx)

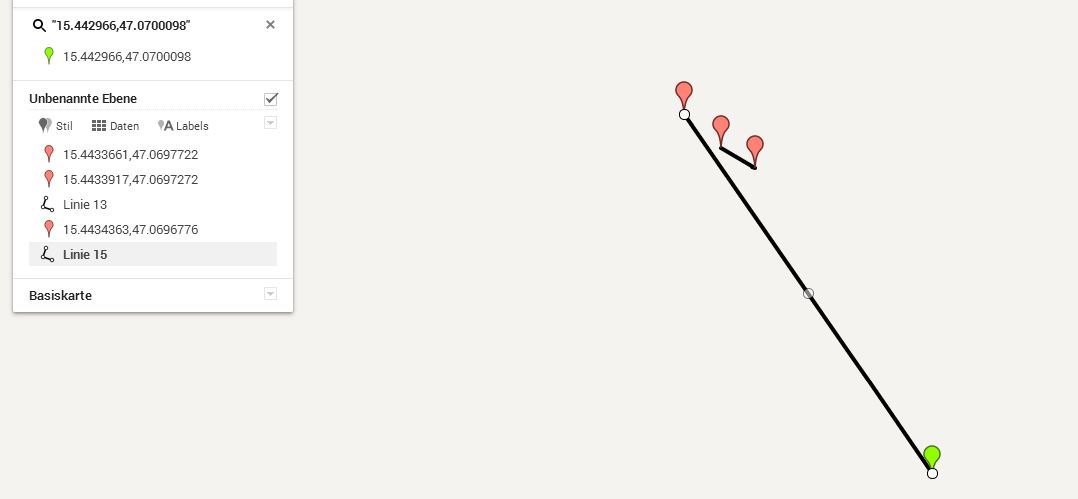
Если я рассчитываю это для следующих заданных координат GPS, я получаю пересечение, если пересечение невозможно.

A: x: 15.4433917 y: 47.0697272

B: x: 15,4433661 y: 47,0697722

С: х: 15,4434363 у: 47,0696776

D: x: 15.442966 y: 47.0700098

Если я нарисую его в Google Maps Engine, я вижу, что между этими линиями точно нет пересечения.

Результаты для dotproductleft: -7.372399999828474E-10 и для dotproductleright: 1.1921940000328E-8

Он хорошо работает с другими примерами, но здесь я видел, что он работает неправильно. Но я не смог обнаружить ни одной ошибки в формуле.

Answer 1

Линии, содержащие любой отрезок (например, AB и CD), всегда будут пересекаться (если они не параллельны).

Вы хотите проверить, пересекаются ли отрезки. Это легко сделать, найдя точку пересечения и проверив, лежит ли она на обоих отрезках.

Итак, используя ваш пример, две линии (на которых лежат отрезки AB и CD) пересекаются при P = (15.4434,47.0697). Теперь, если P лежит на AB, то произведение точек PA и PB отрицательно (поскольку угол между PA и PB составляет 180°, а cos (180°) = - 1).

Если вы вычислите скалярное произведение PA и PB, вы получите положительное число (таким образом, оно не лежит на AB). Тем не менее, скалярное произведение ПК и ПД дает отрицательное число (таким образом, оно находится на CD).

Таким образом, вы можете проверить, пересекаются ли отрезки, если вышеупомянутые точечные произведения (с точкой пересечения) являются отрицательными.