Пользовательское ядро ​​Sklearn дает неправильную функцию принятия решения

Question

Я успешно реализовал собственное линейное ядро, которое отлично работает с clf.predict. Однако, когда я хочу использовать, он дает постоянные значения для всех точек.

Это код кастомного ядра:

      def linear_basis(x, y):
    return np.dot(x.T, y)

def linear_kernel(X, Y, K=linear_basis):
    gram_matrix = np.zeros((X.shape[0], Y.shape[0]))
    for i, x in enumerate(X):
        for j, y in enumerate(Y):
            gram_matrix[i,j] = K(x,y)
        return gram_matrix

Теперь используем это ядро ​​для небольшого линейного обучающего набора.

      #creating random 2D points
sample_size = 100
dat = {
    'x': [random.uniform(-2,2) for i in range(sample_size)],
    'y': [random.uniform(-2,2) for i in range(sample_size)]
}

data = pd.DataFrame(dat)

# giving the random points a linear structure
f_lin = np.vectorize(lambda x, y: 1 if x > y else 0)
data['z_lin'] = f_lin(data['x'].values, data['y'].values)
data_pos = data[data.z_lin == 1.]
data_neg = data[data.z_lin == 0.]

X_train = data[['x', 'y']]
y_train = data[['z_lin']]

clf_costum_lin = svm.SVC(kernel=linear_kernel) # using my costum kernel here
clf_costum_lin.fit(X_train.values,y_train.values)

# creating a 100x100 grid to manually predict each point in 2D
gridpoints = np.array([[i,j] for i in np.linspace(-2,2,100) for j in np.linspace(-2,2,100)])
gridresults = np.array([clf.predict([gridpoints[k]]) for k in range(len(gridpoints))])

# now plotting each point and the training samples
plt.scatter(gridpoints[:,0], gridpoints[:,1], c=gridresults, cmap='RdYlGn')
plt.scatter(data_pos['x'], data_pos['y'], color='green', marker='o', edgecolors='black')
plt.scatter(data_neg['x'], data_neg['y'], color='red', marker='o', edgecolors='black')
plt.show()

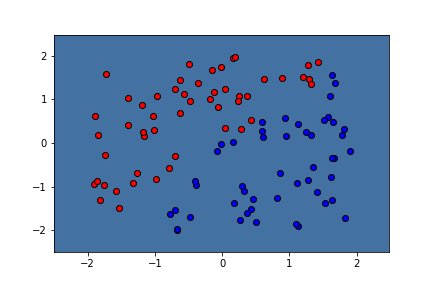
Это дает следующий результат:

Теперь я хочу воспроизвести сюжет, используя clf.decision_function:

(! Обратите внимание, что я случайно поменял цвета здесь!)

      h = .02
xx, yy = np.meshgrid(np.arange(-2 - .5, 2 + .5, h),
    np.arange(-2 - .5, 2 + .5, h))

# using the .decision_function here
Z = clf_costum_lin.decision_function(np.c_[xx.ravel(), yy.ravel()]) 

Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.RdBu, alpha=.8)

plt.scatter(data_pos['x'], data_pos['y'], color='blue', marker='o', edgecolors='black')
plt.scatter(data_neg['x'], data_neg['y'], color='red', marker='o', edgecolors='black')
plt.show()

Это дает следующий сюжет:

Это пример графика тех же данных с использованием интегрированного линейного ядра (kernel="linear"):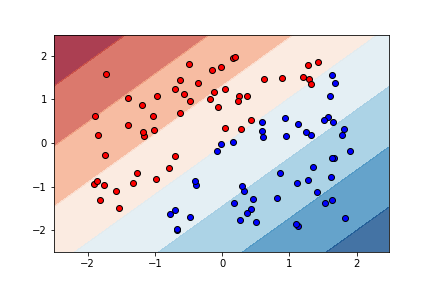

Поскольку функция прогнозирования для настраиваемого ядра только что работала, она должна давать тот же рабочий график с функцией принятия решения, верно? Я понятия не имею, почему это работает с интегрированной линейной функцией, но не с пользовательской линейной функцией, которая также работает только для прогнозирования точек без функции принятия решения. Надеюсь, здесь кто-то может помочь.

Answer 1

Реальная проблема действительно глупая, но, поскольку на ее поиски потребовалось довольно много времени, я поделюсь схемой моей отладки.

Во-первых, вместо построения графика распечатайте фактические значения decision_function: вы обнаружите, что первое получается уникальным, но после этого все остается неизменным. Этот шаблон сохраняется, выполняя то же самое на различных срезах набора данных. Поэтому я подумал, что, возможно, некоторые значения были перезаписаны, и я покопался в SVCнемного кода. Это приводит к некоторым полезным внутренним функциям / атрибутам, например ._BaseLibSVM__Xfit содержащие данные обучения, _decision_function а также _dense_decision_function, а также . Но ни один из кодов не указывал на проблему, и их запуск показал ту же проблему. Бег _compute_kernelдал результаты, которые были нулевыми после первой строки, а затем, возвращаясь к вашему коду, выполнение уже делает это. Итак, наконец, он возвращается к вашему linear_kernel функция.

Вы возвращаетесь внутрь внешнего цикла for, поэтому вы всегда используете только первую строку X, никогда не вычисляя остальную часть матрицы. (Это вызывает удивление: почему прогнозы выглядели хорошо? Похоже, это была случайность. Изменение определения для f_lin, чтобы изменить классы, модель по-прежнему изучает линию slope-1.)