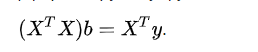Проблема с размерностями матрицы при вычислении метода наименьших квадратов

Question

Моя предыдущая тема в этой области.

Задача решения алгоритма полиномиальной регрессии методом наименьших квадратов в Octave

Я решил не менять основные вопросы, а создать новый вопрос для каждой проблемы.

На этот раз проблема заключается в следующем: я работал методом наименьших квадратов в полиномиальной регрессии.

Дифференцируя эту функцию по вектору параметров b и приравнивая производные нулю, мы получаем систему уравнений (в матричной форме) - эту формулу.

То есть, если я хочу выразить здесь b, мне нужно сделать то, что я сделал.

      b=X^{T}y/(X^{T}X)=> b=X'*y1/(X'*X)

Код:

      #Generating random values ​​of experimental data
x=0:0.1:5;
y=3*x+2;
y1=y+randn(size(y));
k=5;#Polynomial degree
X=[x' ones(length(x),1)];
b=X'*y1/(X'*X); Error: operator *: nonconformant arguments (op1 is 2x51, op2 is 1x51)\

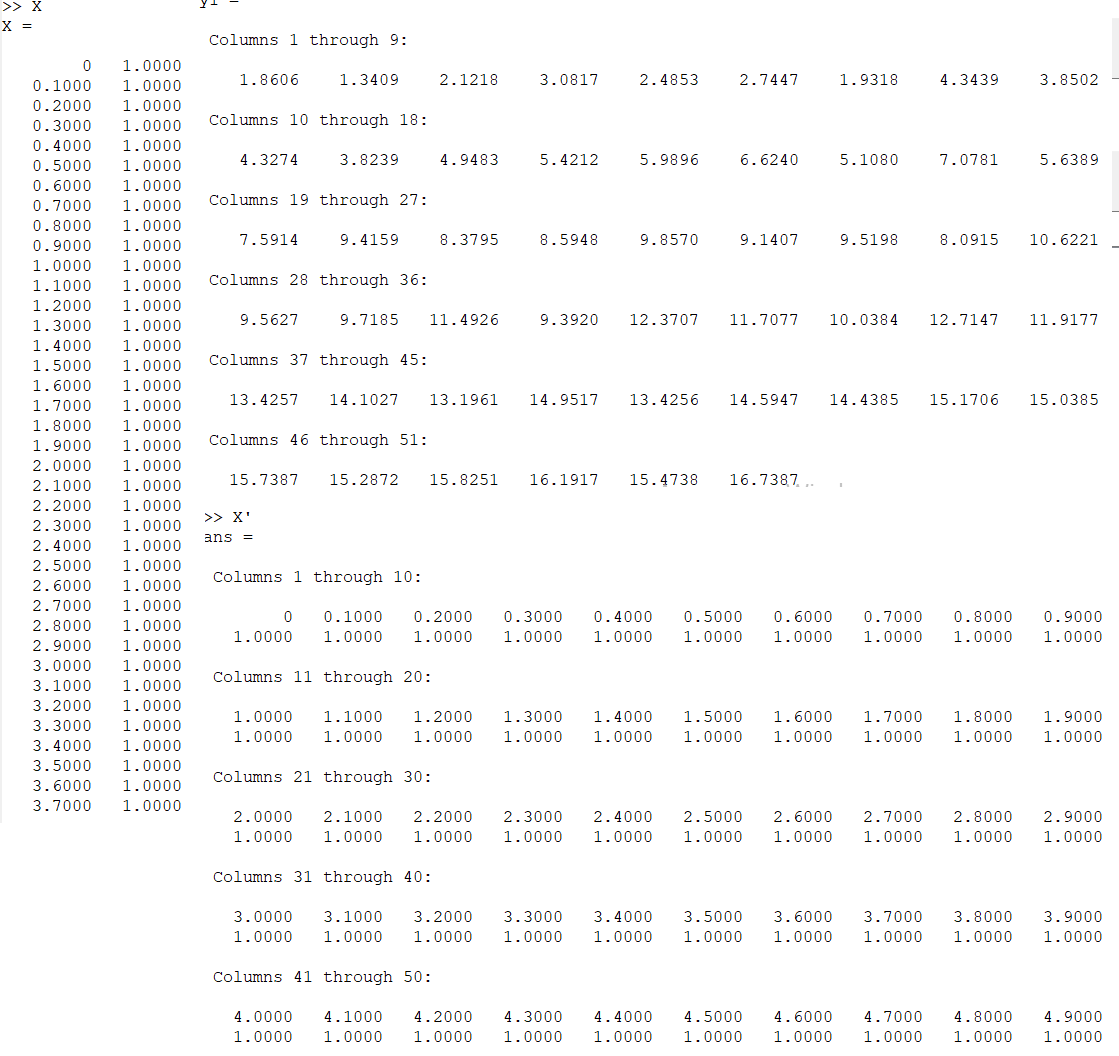
Да, размеры массивов и не совпадают. Прикрепленные скриншоты покажут все. На этом скриншоте переменные X, y1 и X'(транспонированы).

Затем я решил выбрать 1 столбец из массива X и умножьте на.

Если вы посмотрите на скриншоты, то увидите, что теперь транспонированный X' соответствует y1Габаритные размеры. То есть ошибки быть не должно, но она все равно есть.

Answer 1

Вы ошиблись с математикой. Вы не можете просто случайным образом разделить, где хотите, при выполнении матричных операций.

Решение методом наименьших квадратов:

      b=(X'*X)^-1 * X' * y

Также ваше определение y неправильный, или ваш размер не подходит.

      x=0:0.1:5;
y=(3*x+2)'; %transpose!
y1=y+randn(size(y));
X=[x' ones(length(x),1)];

Обратную матрицу никогда не следует принимать численно. К счастью, существует так называемая псевдообратная матрица Мура-Пенроуза, которая гарантирует, что при использовании вы получите решение исходной задачи методом наименьших квадратов. Так что давайте использовать это.

      b=pinv(X'*X)*X'*y;
b_with_noise=pinv(X'*X)*X'*y1;

Обратите внимание, что следующее в основном является нулевым для числовой точности, что означает, что это правильно.

      sum(X*b-y)

ans =

  -5.8176e-14

Теперь в MATLAB / octave вы можете сделать это намного проще:

      b=X\y;
b_with_noise=X\y1;

MATLAB найдет лучший алгоритм для вычисления решения методом наименьших квадратов. mldivide содержит больше информации (октавных документов немного больше, но они должны работать таким же образом).