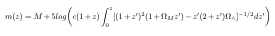Подгонка уравнения с интегралом, где верхний предел является переменной

Question

Я пытаюсь соответствовать уравнению, которое имеет интеграл. Верхний предел интеграла является переменной, и поэтому у меня возникли проблемы с использованием четырехугольника, поскольку он принимает только плавающие числа в качестве пределов. Я пытался обойти это, используя цикл for, но я все еще продолжаю получать ту же ошибку 'ValueError: Истинное значение массива с более чем одним элементом неоднозначно. Используйте a.any() или a.all()'.

Уравнение, которое я пытаюсь подогнать:

Я знаю константы M и c, и у меня есть данные для m(z) и z. Я пытаюсь соответствовать ΩM и ΩΛ. Это мой код:

import numpy as np
import scipy.integrate as integrate
from scipy.optimize import curve_fit

z=[0.03, 0.05, 0.026, 0.075, 0.026, 0.014, 0.101, 0.02, 0.036, 0.045, 0.043, 0.018, 0.079, 
0.088, 0.063, 0.071, 0.052, 0.05]
m=[16.26, 17.63, 16.08, 18.43, 16.28, 14.47, 19.16, 15.18, 16.66, 17.61, 17.19, 15.61, 
18.27, 19.28, 18.24, 18.33, 17.54, 17.69]
c=299792.458 #speed of light
M=-18.316469239 

def integrand(Z,OM,OV):
    return np.power((((1+Z)**2)*(1+OM*Z)-Z*(2+Z)*OV),-0.5)

def curve(z,OM,OV):
    for i in z:
        I=integrate.quad(integrand,0,i,args=(OM,OV))[0]
    return M+5*np.log10(c*(1+z))*I)                       

popts, pcov=curve_fit(curve,z,m)

Заранее спасибо и надеюсь, что это все!

Answer 1

В дополнение к тому, что было прокомментировано, вы учитываете только последний результат цикла интеграции. Исправленный код должен быть таким:

from matplotlib import pylab as plt

import numpy as np
import scipy.integrate as integrate
from scipy.optimize import curve_fit

z=np.asarray([0.03, 0.05, 0.026, 0.075, 0.026, 0.014, 0.101, 0.02, 0.036, 0.045, 0.043, 0.018, 0.079, 
0.088, 0.063, 0.071, 0.052, 0.05])
m=np.asarray([16.26, 17.63, 16.08, 18.43, 16.28, 14.47, 19.16, 15.18, 16.66, 17.61, 17.19, 15.61, 
18.27, 19.28, 18.24, 18.33, 17.54, 17.69])

# sorting of the data is not necessary but nicer when plotting
idx = np.argsort(z)
z = np.take(z, idx)
m = np.take(m, idx)

c=299792458 #speed of light
M=-18.316469239 

def integrand(Z,OM,OV):
    return np.power((((1+Z)**2)*(1+OM*Z)-Z*(2+Z)*OV),-0.5)

def curve(z,OM,OV):
    I = [integrate.quad(integrand,0,i,args=(OM,OV))[0] for i in z]
    return M+5*np.log10(c*(1+z)*I)

popts, pcov=curve_fit(curve,z,m, p0=(1,1))

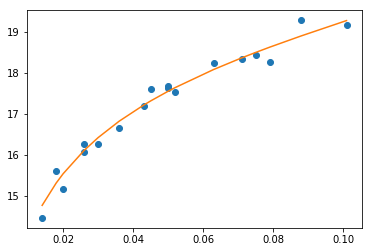
plt.plot(z,m,'o')
plt.plot(z,curve(z,*popts))
plt.show()

И действительно, это дает хорошее соответствие: