Как смоделировать временную реакцию передаточной функции системы с помощью python-control (проблема IVP)?

Question

Я пытаюсь продемонстрировать, как "решать" (моделировать решение) задач начального значения дифференциального уравнения (IVP), используя как определение передаточной функции системы, так и python-controlмодуль. Дело в том, что я новичок в вопросах контроля.

У меня в качестве примера есть простой дифференциал: y'' - 4y' + 13y = 0, с этими начальными условиями: y(0) = 1 и y'(0) = 0.

Я добиваюсь этой передаточной функции вручную: Y(s) = (s - 4)/(s^2 - 4*s + 13).

Итак, на Python я пишу этот небольшой фрагмент кода (обратите внимание, что y_ansэто ответ этой дифференциальной IVP, как показано здесь):

       import numpy as np
import control as ctl
import matplotlib.pyplot as plt

t = np.linspace(0., 1.5, 100)
sys = ctl.tf([1.,-4.],[1.,-4.,13.])
T, yout, _ = ctl.forced_response(sys, T=t, X0=[1, 0])

y_ans = lambda x: 1/3*np.exp(2*x)*(3*np.cos(3*x) - 2*np.sin(3*x))

plt.plot(t, y_ans(t), '-.', color='gray', alpha=0.5, linewidth=3, label='correct answer')
plt.plot(T, yout, 'r', label='simulated')
plt.legend()

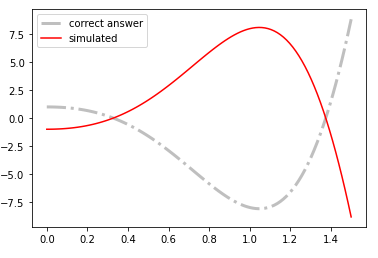
Этот код дает мне этот график:

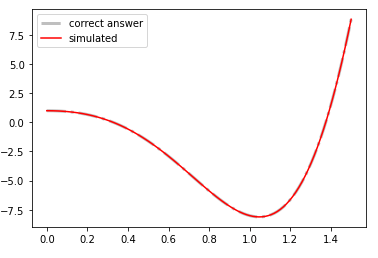
Но когда я вставляю отрицательный знак перед yout, У меня есть совпадение, как хотелось бы:

       plt.plot(T, -yout, 'r', label='simulated') ### yout with negative sign

Что я делаю неправильно? Документация по Python-control мне не очень понятна. Кроме того, я не знаю, насколько моя интерпретация X0 параметр для control.forced_responseверно. Можно ли сделать это так, как я задумал?

Любой, кто может пролить свет на эту тему, может внести свой вклад.

РЕДАКТИРОВАТЬ

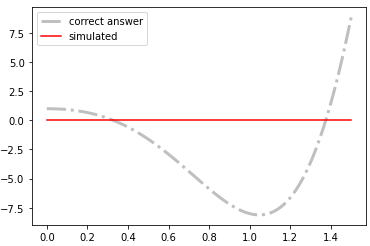
Настройка X0 = [0,0] дает мне этот график:

Answer 1

Я думаю, что лучше всего здесь преобразовать вашу систему в пространство состояний и посмотреть, что происходит (существует множество возможных представлений пространства состояний):

      sys_tf = ctl.tf([1.,-4.],[1.,-4.,13.])
sys_ss = ctl.tf2ss(sys_tf)
print(sys_ss)

Выход:

      A = [[ 4.00000000e+00  1.30000000e+00]
     [-1.00000000e+01  1.33226763e-15]]

B = [[-1.]
     [ 0.]]

C = [[-1.  -0.4]]

D = [[0.]]

Мы хотим найти x(0) такой, что y(0) = Cx(0) = 1 и y'(0) = CAx(0) = 0.

Мы можем либо записать эти уравнения и решить их вручную, либо использовать линейную алгебру:

      A = np.vstack([sys_ss.C, sys_ss.C @ sys_ss.A])
b = np.array([[1], [0]])
x0 = np.linalg.solve(A, b)
print(x0)

дает:

      [[-1.00000000e+00]
 [-1.36642834e-15]]

Следовательно, это должно работать:

      T, yout = ctl.forced_response(sys_ss, T=t, X0=[-1, 0])

Кроме того, поскольку вас интересует только переходная реакция на начальное условие (т. Е. u(t)=0) вы можете использовать initial_response функция:

      T, yout = ctl.initial_response(sys_ss, T=t, X0=[-1, 0])

Answer 2

Благодаря комментарию @LutzLehmann, я думаю о значении слова "дважды кодировать" некоторые вещи. Итак, возвращаясь к исходной точке, я понял, что эта передаточная функция включает в себя как входные (время или линейное изменение), так и начальные условия. Фактически это выход. Мне нужно какое-то обратное преобразование Лапласа или, как я начинаю думать, мне нужно только смоделировать его как есть, без дополнительной информации.

Таким образом, мне удалось использовать импульсный вход (преобразование Лапласа равно 1), и я смог получить выходной сигнал, который точно соответствовал моему tf, смоделированному во времени.

       import numpy as np
import control as ctl
import matplotlib.pyplot as plt

t = np.linspace(0., 1.5, 100)
sys = ctl.tf([1.,-4.],[1.,-4.,13.])
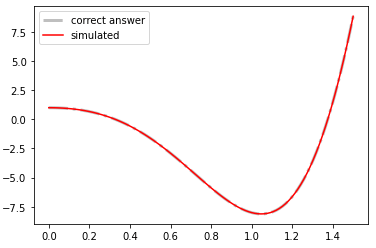
T, yout = ctl.impulse_response(sys, T=t) # HERE is what I wanted

y_ans = lambda x: 1/3*np.exp(2*x)*(3*np.cos(3*x) - 2*np.sin(3*x))

plt.plot(t, y_ans(t), '-.', color='gray', alpha=0.5, linewidth=3, label='correct answer')
plt.plot(T, yout, 'r', label='simulated')
plt.legend()

Теперь я думаю, что могу показать, как использовать python-control для косвенного моделирования ответов для дифференциальных уравнений.:-D