Построение решений для дифференциальных уравнений, но не по времени в MATLAB

Question

Мой вопрос сегодня связан с этим предыдущим вопросом. Я следую за этой исследовательской работой. Я пытаюсь продублировать рисунок 8, расположенный на странице 20. У меня есть скриншот: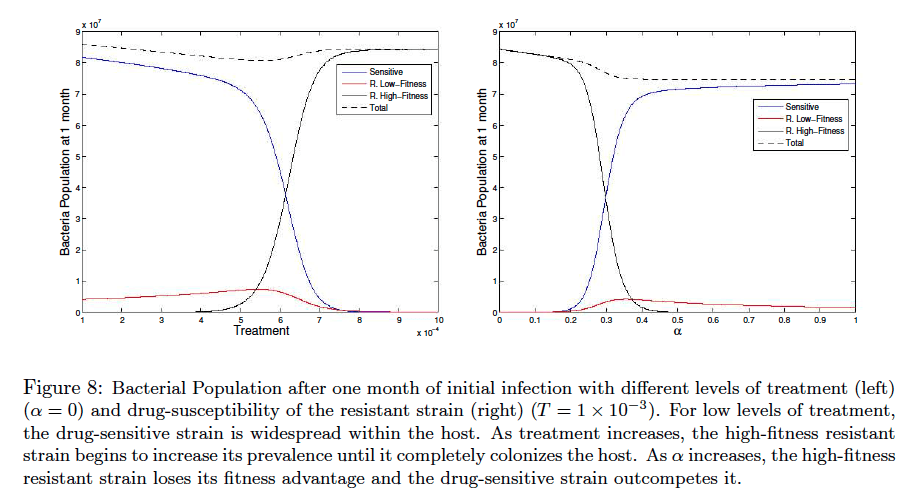

Я запутался в том, как изобразить левую фигуру в MATLAB, потому что теперь вместо изменения времени у нас меняется лечение. Вот что у меня есть из предыдущего вопроса:

function dX = CompetitionModel(~,X)       
  bs = 8e-3; 
  bl = 4e-3; 
  bh = 6.4e-3;
  N = sum(X);  
  K = 1e8;
  m1 = 2e-5; 
  m2 = 9e-9; 
  p = 5e-13; 
  I = 1e-3; 
  T = 1e-3; % Treatment
  a = 0; 
  dX = [X(1) * (bs * (1 - N/K) - I - T - m1) - p * X(1) * (X(2) + X(3));
       X(2) * (bl * (1 - N/K) - I - a*T - m2) + m1 * X(1) + p * X(2) * (X(1) - X(3));
       X(3) * (bh * (1 - N/K) - I - a*T) + m2 * X(2) + p * X(3) * (X(1) + X(2))];
end

Чтобы построить мои уравнения в предыдущем вопросе, я набрал в командной строке следующее:

>> [t,Y] = ode45(@CompetitionModel, [0 4.5e4], [1e4 0 0]);
>> plot(t,X(:,1), t,X(:,2), t,X(:,3))

В моем функциональном файле у меня уже определена обработка. Я предполагаю, что это не должно быть больше. Так что я могу сделать, чтобы лечение менялось во времени? Я надеюсь, что мой вопрос имеет смысл.

Answer 1

Вы по-прежнему решаете уравнение относительно времени - но только наносите на график значение в момент времени t = 1 месяц. Чтобы изменить обработку, вам необходим дополнительный цикл вокруг вызова ode45 и передача текущего значения обработки в функцию dX

for treatment = 10^-4:10^-5:10^-3
    [t,Y] = ode45(@CompetitionModel, [0 4.5e4], [1e4 0 0], [] , treatment);
    plot(treatment,Y(end,1), 'x')
    plot(treatment,Y(end,2), 'kx')
    plot(treatment,Y(end,3), 'rx')
    hold on
end

теперь необходимо изменить функцию dX, чтобы она принимала ввод лечения:

function dX = CompetitionModel(~,X, T)       

Наконец, прокомментируйте свое старое назначение лечения в функции dX: %T = 1e-3; % Лечение