Как построить решения системы нелинейных дифференциальных уравнений в MATLAB?

Question

Я пытаюсь следовать этой исследовательской работе. Я пытаюсь продублировать график решений, показанных на рис. 7 на стр. 20. У меня есть скриншот с рис. 7:

Сначала я хотел бы воссоздать левую картинку. Рассматриваемая система - это то, что у меня есть dX, Вот что у меня есть в m-файле:

function dX = CompetitionModel(t,X)       
  bs = 8*10^(-3); 
  bl = 4*10^(-3); 
  bh = 6.4*10^(-3);
  N = bs + bl + bh;
  K = 10^8;
  m1 = 2*10^(-5); 
  m2 = 9*10^(-9); 
  p = 5*10^(-13); 
  I = 10^(-3); 
  T = 0; 
  a = 0; 
  dX = [X(1) * (bs * (1 - N/K) - I - T - m1) - p * X(1) * (X(2) + X(3));
       X(2) * (bl * (1 - N/K) - I - a*T - m2) + m1 * X(1) + p * X(2) * (X(1) - X(3));
       X(3) * (bh * (1 - N/K) - I - a*T) + m2 * X(2) + p * X(3) * (X(1) + X(2))];
end

ode45 имеет синтаксис: [T,Y] = solver(odefun,tspan,y0), Я получаю tspan с картинки, которую я разместил. Мои начальные условия:S0 = 10^4; Rl0 = 0; Rh0 = 0так вот что у меня как y0, Я набираю следующее в командном окне:

>>[t,X1] = ode45('CompetitionModel', [0,45000], [10^4, 0, 0]);
>>[t,X2] = ode45('CompetitionModel', [0,45000], [10^4, 0, 0]);
>>[t,X3] = ode45('CompetitionModel', [0,45000], [10^4, 0, 0]);

MATLAB был занят последние 30 минут, и мой ноутбук начинает сильно нагреваться. Так что я не могу приступить к построению графика, пока он не закончится, и я не знаю, есть ли какие-либо ошибки в моем коде. Мне было интересно, если есть, возможно, лучший способ, которым я мог бы получить решения системы dX,

Answer 1

Я проверил ODE по бумаге и обнаружил одну ошибку. Согласно последнему абзацу страницы 9 в документе, N = S + Rl + Rh, Исправленный код:

function dX = CompetitionModel(~,X)       
  bs = 8e-3; 
  bl = 4e-3; 
  bh = 6.4e-3;
  N = sum(X);  % this line was incorrect
  K = 1e8;
  m1 = 2e-5; 
  m2 = 9e-9; 
  p = 5e-13; 
  I = 1e-3; 
  T = 0;
  a = 0; 
  dX = [X(1) * (bs * (1 - N/K) - I - T - m1) - p * X(1) * (X(2) + X(3));
       X(2) * (bl * (1 - N/K) - I - a*T - m2) + m1 * X(1) + p * X(2) * (X(1) - X(3));
       X(3) * (bh * (1 - N/K) - I - a*T) + m2 * X(2) + p * X(3) * (X(1) + X(2))];

Обратите внимание на пару синтаксических изменений. Во-первых, поскольку вы на самом деле не используете значение времени в вашем ODE, вы можете оставить ~ вместо t что вы имели в своем определении функции в качестве замены для неиспользуемого ввода. Во-вторых, вы можете использовать обозначение 8e-3 вместо 8*10^(-3), Они оценивают одно и то же, но первый выглядит немного чище.

Участок без обработки, т.е. T = 0, показано ниже.

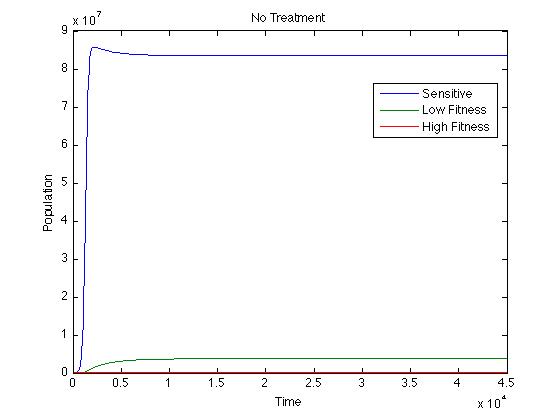
Я выяснил проблему в ODE, сначала попытавшись решить ваше уравнение с некоторыми жесткими решателями ODE в MATLAB. См. Документацию по MATLAB ODE для получения более подробной информации. В основном я решил это с ode15s а также ode23s и обнаружил, что решение было нестабильным (население ушло в бесконечность). Эти другие решатели - хорошие инструменты, о которых нужно помнить, если ваше решение зависает; иногда один из других будет работать, и он либо даст вам то, что вы хотите, либо укажет, что у вас есть другая проблема в другом месте.

Примечание: я совершенно уверен, что вы не правильно используете "фазовый портрет" здесь. Вы просто ищете решение ODE относительно времени с заданным набором начальных условий. Фазовый портрет смотрит на то, как состояния системы (ваши три разные популяции здесь) развиваются при разных наборах начальных условий. Он ничего не показывает о зависимости этих решений от времени, а только о том, как они развиваются относительно друг друга.