Визуальное сравнение регрессии и PCA
Я пытаюсь усовершенствовать метод сравнения регрессии и PCA, вдохновленный блогом Cerebral Mastication, который также обсуждался с другой точки зрения на SO. Прежде чем я забуду, большое спасибо JD Long и Josh Ulrich за большую часть этого. Я собираюсь использовать это в курсе следующего семестра. Извините, это долго!
ОБНОВЛЕНИЕ: я нашел другой подход, который почти работает (пожалуйста, исправьте это, если можете!). Я разместил это внизу. Гораздо умнее и короче, чем я смог придумать!
Я в основном следовал предыдущим схемам до определенного момента: генерировать случайные данные, определять линию наилучшего соответствия, рисовать остатки. Это показано во втором фрагменте кода ниже. Но я также покопался и написал несколько функций для рисования линий, перпендикулярных линии, проходящей через случайную точку (в данном случае это точки данных). Я думаю, что они работают нормально, и они показаны в First Code Chunk вместе с доказательством того, что они работают.
Второй блок кода показывает все в действии, используя тот же поток, что и @JDLong, и я добавляю изображение получающегося графика. Данные черного цвета, красный - регрессия с остатками розового, синий - 1-й ПК, а светло-голубой - нормали, но, очевидно, это не так. Функции в First Code Chunk, которые рисуют эти нормали, кажутся нормальными, но что-то не так с демонстрацией: я думаю, что я что-то неправильно понимаю или передаю неправильные значения. Мои нормали поступают по горизонтали, что кажется полезной подсказкой (но пока не для меня). Кто-нибудь может увидеть, что здесь не так?
Спасибо, это меня некоторое время раздражало...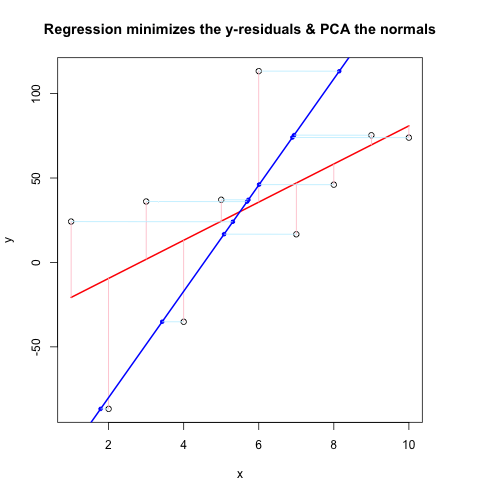
Первый блок кода (функции для рисования норм и доказательства их работы):
##### The functions below are based very loosely on the citation at the end
pointOnLineNearPoint <- function(Px, Py, slope, intercept) {
# Px, Py is the point to test, can be a vector.
# slope, intercept is the line to check distance.
Ax <- Px-10*diff(range(Px))
Bx <- Px+10*diff(range(Px))
Ay <- Ax * slope + intercept
By <- Bx * slope + intercept
pointOnLine(Px, Py, Ax, Ay, Bx, By)
}
pointOnLine <- function(Px, Py, Ax, Ay, Bx, By) {
# This approach based upon comingstorm's answer on
# stackru.com/questions/3120357/get-closest-point-to-a-line
# Vectorized by Bryan
PB <- data.frame(x = Px - Bx, y = Py - By)
AB <- data.frame(x = Ax - Bx, y = Ay - By)
PB <- as.matrix(PB)
AB <- as.matrix(AB)
k_raw <- k <- c()
for (n in 1:nrow(PB)) {
k_raw[n] <- (PB[n,] %*% AB[n,])/(AB[n,] %*% AB[n,])
if (k_raw[n] < 0) { k[n] <- 0
} else { if (k_raw[n] > 1) k[n] <- 1
else k[n] <- k_raw[n] }
}
x = (k * Ax + (1 - k)* Bx)
y = (k * Ay + (1 - k)* By)
ans <- data.frame(x, y)
ans
}
# The following proves that pointOnLineNearPoint
# and pointOnLine work properly and accept vectors
par(mar = c(4, 4, 4, 4)) # otherwise the plot is slightly distorted
# and right angles don't appear as right angles
m <- runif(1, -5, 5)
b <- runif(1, -20, 20)
plot(-20:20, -20:20, type = "n", xlab = "x values", ylab = "y values")
abline(b, m )
Px <- rnorm(10, 0, 4)
Py <- rnorm(10, 0, 4)
res <- pointOnLineNearPoint(Px, Py, m, b)
points(Px, Py, col = "red")
segments(Px, Py, res[,1], res[,2], col = "blue")
##========================================================
##
## Credits:
## Theory by Paul Bourke http://local.wasp.uwa.edu.au/~pbourke/geometry/pointline/
## Based in part on C code by Damian Coventry Tuesday, 16 July 2002
## Based on VBA code by Brandon Crosby 9-6-05 (2 dimensions)
## With grateful thanks for answering our needs!
## This is an R (http://www.r-project.org) implementation by Gregoire Thomas 7/11/08
##
##========================================================
Второй блок кода (готовит демонстрацию):
set.seed(55)
np <- 10 # number of data points
x <- 1:np
e <- rnorm(np, 0, 60)
y <- 12 + 5 * x + e
par(mar = c(4, 4, 4, 4)) # otherwise the plot is slightly distorted
plot(x, y, main = "Regression minimizes the y-residuals & PCA the normals")
yx.lm <- lm(y ~ x)
lines(x, predict(yx.lm), col = "red", lwd = 2)
segments(x, y, x, fitted(yx.lm), col = "pink")
# pca "by hand"
xyNorm <- cbind(x = x - mean(x), y = y - mean(y)) # mean centers
xyCov <- cov(xyNorm)
eigenValues <- eigen(xyCov)$values
eigenVectors <- eigen(xyCov)$vectors
# Add the first PC by denormalizing back to original coords:
new.y <- (eigenVectors[2,1]/eigenVectors[1,1] * xyNorm[x]) + mean(y)
lines(x, new.y, col = "blue", lwd = 2)
# Now add the normals
yx2.lm <- lm(new.y ~ x) # zero residuals: already a line
res <- pointOnLineNearPoint(x, y, yx2.lm$coef[2], yx2.lm$coef[1])
points(res[,1], res[,2], col = "blue", pch = 20) # segments should end here
segments(x, y, res[,1], res[,2], col = "lightblue1") # the normals
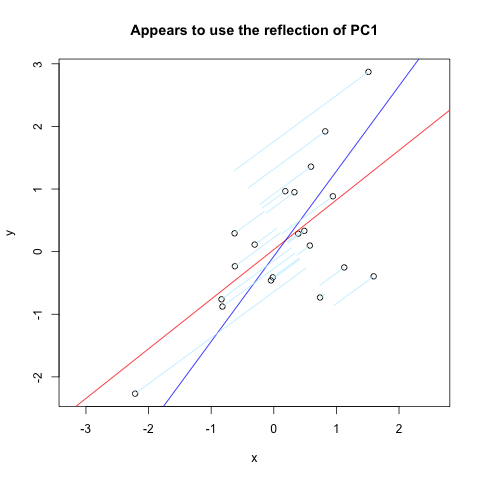
На странице Винсента Зоонекенда я нашел почти то, что хотел. Но это не совсем работает (очевидно, раньше работал). Вот фрагмент кода с этого сайта, который отображает нормали к первому ПК, отраженному через вертикальную ось:
set.seed(1)
x <- rnorm(20)
y <- x + rnorm(20)
plot(y~x, asp = 1)
r <- lm(y~x)
abline(r, col='red')
r <- princomp(cbind(x,y))
b <- r$loadings[2,1] / r$loadings[1,1]
a <- r$center[2] - b * r$center[1]
abline(a, b, col = "blue")
title(main='Appears to use the reflection of PC1')
u <- r$loadings
# Projection onto the first axis
p <- matrix( c(1,0,0,0), nrow=2 )
X <- rbind(x,y)
X <- r$center + solve(u, p %*% u %*% (X - r$center))
segments( x, y, X[1,], X[2,] , col = "lightblue1")
И вот результат:
3 ответа
Хорошо, я должен ответить на свой вопрос! После дальнейшего чтения и сравнения методов, которые люди выкладывают в Интернете, я решил проблему. Я не уверен, что могу четко заявить, что я "исправил", потому что я прошел довольно много итераций. Во всяком случае, здесь сюжет и код (MWE). Вспомогательные функции в конце для ясности.
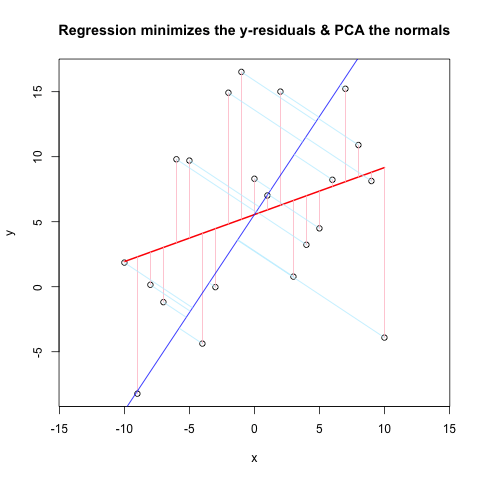
# Comparison of Linear Regression & PCA
# Generate sample data
set.seed(39) # gives a decent-looking example
np <- 10 # number of data points
x <- -np:np
e <- rnorm(length(x), 0, 10)
y <- rnorm(1, 0, 2) * x + 3*rnorm(1, 0, 2) + e
# Plot the main data & residuals
plot(x, y, main = "Regression minimizes the y-residuals & PCA the normals", asp = 1)
yx.lm <- lm(y ~ x)
lines(x, predict(yx.lm), col = "red", lwd = 2)
segments(x, y, x, fitted(yx.lm), col = "pink")
# Now the PCA using built-in functions
# rotation = loadings = eigenvectors
r <- prcomp(cbind(x,y), retx = TRUE)
b <- r$rotation[2,1] / r$rotation[1,1] # gets slope of loading/eigenvector 1
a <- r$center[2] - b * r$center[1]
abline(a, b, col = "blue") # Plot 1st PC
# Plot normals to 1st PC
X <- pointOnLineNearPoint(x, y, b, a)
segments( x, y, X[,1], X[,2], col = "lightblue1")
###### Needed Functions
pointOnLineNearPoint <- function(Px, Py, slope, intercept) {
# Px, Py is the point to test, can be a vector.
# slope, intercept is the line to check distance.
Ax <- Px-10*diff(range(Px))
Bx <- Px+10*diff(range(Px))
Ay <- Ax * slope + intercept
By <- Bx * slope + intercept
pointOnLine(Px, Py, Ax, Ay, Bx, By)
}
pointOnLine <- function(Px, Py, Ax, Ay, Bx, By) {
# This approach based upon comingstorm's answer on
# stackru.com/questions/3120357/get-closest-point-to-a-line
# Vectorized by Bryan
PB <- data.frame(x = Px - Bx, y = Py - By)
AB <- data.frame(x = Ax - Bx, y = Ay - By)
PB <- as.matrix(PB)
AB <- as.matrix(AB)
k_raw <- k <- c()
for (n in 1:nrow(PB)) {
k_raw[n] <- (PB[n,] %*% AB[n,])/(AB[n,] %*% AB[n,])
if (k_raw[n] < 0) { k[n] <- 0
} else { if (k_raw[n] > 1) k[n] <- 1
else k[n] <- k_raw[n] }
}
x = (k * Ax + (1 - k)* Bx)
y = (k * Ay + (1 - k)* By)
ans <- data.frame(x, y)
ans
}
Попробуйте изменить эту строку вашего кода:
res <- pointOnLineNearPoint(x, y, yx2.lm$coef[2], yx2.lm$coef[1])
в
res <- pointOnLineNearPoint(x, new.y, yx2.lm$coef[2], yx2.lm$coef[1])
Итак, вы называете правильные значения y.
В коде Винсента Зоонекенда измените строку u <- r$loadings в u <- solve(r$loadings), Во втором случае solve()прогнозируемые оценки компонентов по первой главной оси (то есть матрицу прогнозированных оценок с вторыми прогнозными оценками компонентов, установленными в ноль) необходимо умножить на обратную величину нагрузок / собственных векторов. Умножение данных на нагрузки дает прогнозные оценки; деление прогнозируемых баллов на нагрузки дает данные. Надеюсь, это поможет.