2D поворот изображения

Question

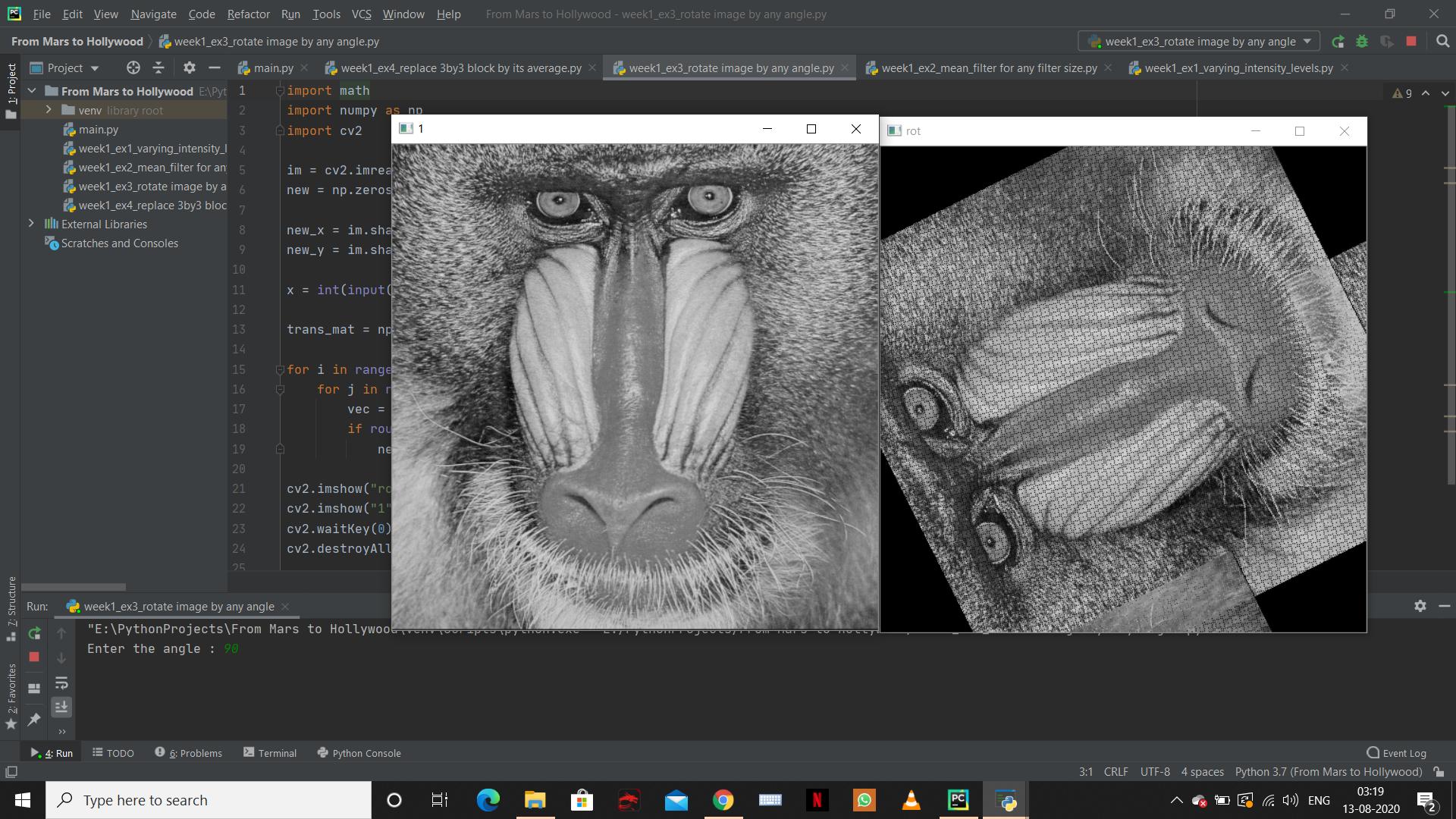Я пытаюсь повернуть изображение на любой заданный угол. Я вращаюсь, используя центр изображения в качестве начала координат.

Но код не выполняет ротацию, как ожидалось. Прилагаю код ниже.

import math
import numpy as np
import cv2

im = cv2.imread("Samples\\baboon.jpg", cv2.IMREAD_GRAYSCALE)
new = np.zeros(im.shape,np.uint8)

new_x = im.shape[0] // 2
new_y = im.shape[1] // 2

x = int(input("Enter the angle : "))

trans_mat = np.array([[math.cos(x), math.sin(x), 0],[-math.sin(x), math.cos(x), 0],[0, 0, 1]])

for i in range(-new_x, im.shape[0] - new_x):
    for j in range(-new_y, im.shape[1] - new_y):
        vec = np.matmul([i, j, 1], trans_mat)
        if round(vec[0] + new_x) < 512 and round(vec[1] + new_y) < 512:
            new[round(vec[0]+new_x), round(vec[1]+new_y)] = im[i+new_x,j+new_y]

cv2.imshow("rot",new)
cv2.imshow("1",im)
cv2.waitKey(0)
cv2.destroyAllWindows()

Answer 1

Похоже, вы пытаетесь реализовать ресамплер ближайшего соседа. Вы просматриваете изображение и сопоставляете каждый входной пиксель с новым местом в выходном изображении. Это может привести к таким проблемам, как неправильная перезапись пикселей друг друга, оставление выходных пикселей пустыми и т.п.

Я бы посоветовал (исходя из опыта) посмотреть на проблему задом наперед. Вместо того, чтобы смотреть на то, где входной пиксель заканчивается на выходе, вы должны учитывать, где каждый выходной пиксель берет начало на входе. Таким образом, у вас не будет двусмысленности в отношении ближайших соседей, и весь массив изображений будет заполнен.

Вы хотите повернуться вокруг центра. Текущая матрица вращения, которую вы используете, вращается вокруг(0, 0). Чтобы это компенсировать, вам нужно перевести центр изображения в(0, 0), повернуть, а затем перевести обратно. Вместо того, чтобы разрабатывать полную аффинную матрицу, я покажу вам, как выполнять отдельные операции вручную, а затем как объединить их в матрицу преобразования.

Ручное вычисление

Сначала получите изображение ввода и вывода:

im = cv2.imread("Samples\\baboon.jpg", cv2.IMREAD_GRAYSCALE)
new = np.zeros_like(im)

Затем определите центр вращения. Будьте ясны в своих размерахx обычно столбец (тусклый 1), а не ряд (тусклый 0):

center_row = im.shape[0] // 2
center_col = im.shape[1] // 2

Вычислите радиальные координаты каждого пикселя изображения, имеющего форму соответствующего размера:

row_coord = np.arange(im.shape[0])[:, None] - center_row
col_coord = np.arange(im.shape[1]) - center_col

row_coord а также col_coord- это расстояния от центра выходного изображения. Теперь вычислите места, откуда они пришли во входных данных. Обратите внимание, что мы можем использовать широковещательную рассылку, чтобы избежать цикла. Я следую вашему исходному соглашению для определения углов здесь и нахожу обратное вращение для определения исходного местоположения. Большая разница здесь в том, что входные данные в градусах преобразуются в радианы, поскольку это то, что ожидают тригонометрические функции:

angle = float(input('Enter Angle in Degrees: ')) * np.pi / 180.0 
source_row = row_coord * np.cos(angle) - col_coord * np.sin(angle) + center_row
source_col = row_coord * np.sin(angle) + col_coord * np.cos(angle) + center_col

Если бы все индексы гарантированно попадали во входное изображение, вам даже не нужно было бы заранее выделять выходные. Вы могли буквально просто сделатьnew = im[source_row, source_col]. Однако вам нужно замаскировать индексы:

mask = source_row >= 0 & source_row < im.shape[0] & source_col >= 0 & source_col < im.shape[1]
new[mask] = im[source_row[mask].round().astype(int), source_col[mask].round().astype(int)]

Аффинные преобразования

Теперь давайте посмотрим на использование аффинных преобразований. Сначала вы хотите вычесть центр из ваших координат. Допустим, у вас есть вектор-столбец[[r], [c], [1]]. Перевод к нулю будет матрицей

[[r']    [[1  0 -rc]  [[r]
 [c']  =  [0  1 -cc] . [c]
 [1 ]]    [0  0  1 ]]  [1]]

Затем применяется вращение (назад):

[[r'']    [[cos(a) -sin(a) 0]  [[r']
 [c'']  =  [sin(a)  cos(a) 0] . [c']
 [ 1 ]]    [  0       0    1]]  [1 ]]

И, наконец, нужно перевести обратно в центр:

[[r''']    [[1  0 rc]  [[r'']
 [c''']  =  [0  1 cc] . [c'']
 [ 1  ]]    [0  0  1]]  [ 1 ]]

Если вы перемножите эти три матрицы справа налево, вы получите

   [[cos(a)   -sin(a)    cc * sin(a) - rc * cos(a) + rc]
M = [sin(a)    cos(a)   -cc * cos(a) - rc * sin(a) + cc]
    [  0         0                      1              ]]

Если вы построите полную матрицу выходных координат, а не массивы подмножеств, с которых мы начали, вы можете использовать np.matmul, также известный как @оператор, чтобы сделать умножение за вас. Однако для такого простого случая нет необходимости в таком уровне сложности:

matrix = np.array([[np.cos(angle), -np.sin(angle),  col_center * np.sin(angle) - row_center * np.cos(angle) + row_center],
                   [np.sin(angle),  np.cos(angle), -col_center * np.cos(angle) - row_center * np.sin(angle) + col_center],
                   [0, 0, 1]])

coord = np.ones((*im.shape, 3, 1))
coord[..., 0, :] = np.arange(im.shape[0]).reshape(-1, 1, 1, 1)
coord[..., 1, :] = np.arange(im.shape[1]).reshape(-1, 1, 1)

source = (matrix @ coord)[..., :2, 0]

Остальная часть обработки очень похожа на ручные вычисления:

mask = (source >= 0 & source_row < im.shape).all(axis=-1)
new[mask] = im[source[0, mask].round().astype(int), source_col[1, mask].round().astype(int)]

Answer 2

Я попытался реализовать метод умножения матриц Мадфизика. Вот реализация для тех, кому не все равно:

      import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path

path = Path(".")
img = plt.imread(path.resolve().parent / "img_align" / "faces_imgs" / "4.jpg")
angle = 15


def _transform(rot_mat, x, y):
    """
    conveninece method for matrix multiplication
    """
    return np.matmul(rot_mat, np.array([x, y, 1]))


def rotate(img, angle):
    angle = np.radians(angle)
    new = np.zeros_like(img)
    cx, cy = tuple(x / 2 for x in img.shape[:2])

    rot_mat = np.array(
        [
            [np.cos(angle), -np.sin(angle), 0],
            [np.sin(angle), np.cos(angle), 0],
            [0, 0, 1],
        ]
    )

    rot_mat[0, 2], rot_mat[1, 2], _ = _transform(rot_mat, -cx, -cy)

    # build combined affine transformation matrrix
    rot_mat[0, 2] += cx
    rot_mat[1, 2] += cy

    coord = np.ones((*img.shape, 3, 1))  # [576x336x3x3x1]
    coord[..., 0, :] = np.arange(img.shape[0]).reshape(-1, 1, 1, 1)
    coord[..., 1, :] = np.arange(img.shape[1]).reshape(-1, 1, 1)

    source = (rot_mat @ coord)[..., :2, 0]
    x_mask = source[..., 0] < img.shape[0]
    y_mask = source[..., 1] < img.shape[1]
    xy_mask = np.concatenate([x_mask[..., None], y_mask[..., None]], axis=-1)
    mask = ((source >= 0) & (xy_mask)).all(axis=-1)
    xx = (source[..., 0][mask]).round().astype(int)
    yy = (source[..., 1][mask]).round().astype(int)

    # IndexError handling at border
    if xx.max() == img.shape[0]:
        xx[xx == xx.max()] = xx.max() - 1
    if yy.max() == img.shape[1]:
        yy[yy == yy.max()] = yy.max() - 1
    # Copy pixels
    new[xx, yy] = img[xx, yy]
    plt.imsave("test.jpg", new)


if __name__ == "__main__":
    rotate(img, angle)

Answer 3

Я думаю, это то, что вы ищете. Правильно повернуть изображение в OpenCV?

Вот код

ang = int(input("Enter the angle : "))
im = cv2.imread("Samples\\baboon.jpg", cv2.IMREAD_GRAYSCALE)


def rotimage(image):
    row,col = image.shape[0:2]
    center=tuple(np.array([col,row])/2)
    rot_mat = cv2.getRotationMatrix2D(center,ang,1.0)
    new_image = cv2.warpAffine(image, rot_mat, (col,row))
    return new_image


new_image = rotimage(im)
cv2.imshow("1",new_image)
cv2.waitKey(0)