В Python: как составить бифуркационную диаграмму системы Лоренца при изменении значения параметра?
Итак, я видел закодированное решение своего вопроса в Mathematica, но, имея очень слабое понимание математики, я еще не смог его воспроизвести.
Это то, что я пытаюсь сделать с Python: https://mathematica.stackexchange.com/questions/159211/how-to-make-a-bifurcation-diagram-of-the-lorenz-system-under-a-varying-parameter
Я думаю, что мои ошибки заключаются в понимании того, как рассчитать то, что я ищу, и как настроить мою визуализацию, чтобы она выглядела так же, как в ссылке, но любые идеи приветствуются.
Код, который у меня есть до сих пор, выглядит так:
def lorenz_system(x,y,z,r,s=10,b=6):
x_dot = s*(y-x)
y_dot = r*x-y-x*z
z_dot = x*z-b*z
return x_dot, y_dot, z_dot
dr = 0.1 # parameter step size
r=np.arange(40,200,dr) # parameter range
dt = 0.001 # time step
t = np.arange(0,10,dt) # time range
#initialize solution arrays
xs = np.empty(len(t) + 1)
ys = np.empty(len(t) + 1)
zs = np.empty(len(t) + 1)
#initial values x0,y0,z0 for the system
xs[0], ys[0], zs[0] = (1, 1, 1)
for R in r:
for i in range(len(t)):
#approximate numerical solutions to system
x_dot, y_dot, z_dot = lorenz_system(xs[i], ys[i], zs[i],R)
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
#calculate and plot the peak values of the z solution
for i in range(0,len(zs)-1):
#using only the positive values in the z solution
if zs[i]>0:
#find the local maxima
if (zs[i-1] < zs[i] and zs[i] > zs[i+1]):
if (zs[i]<=1000):
#plot the local maxima point of the z solution that used the parameter R in r
plt.scatter(R,zs[i], color='black')
plt.xlim(0,200)
plt.ylim(0,400)
1 ответ
Ошибка в lorenz_system функция, это должно быть z_dot = x * y - b * z.
Связанный ответ также "использует окончательные значения из одного прогона в качестве начальных условий для следующего, как простой способ оставаться рядом с аттрактором." И отображает как локальные минимумы, так и локальные максимумы.
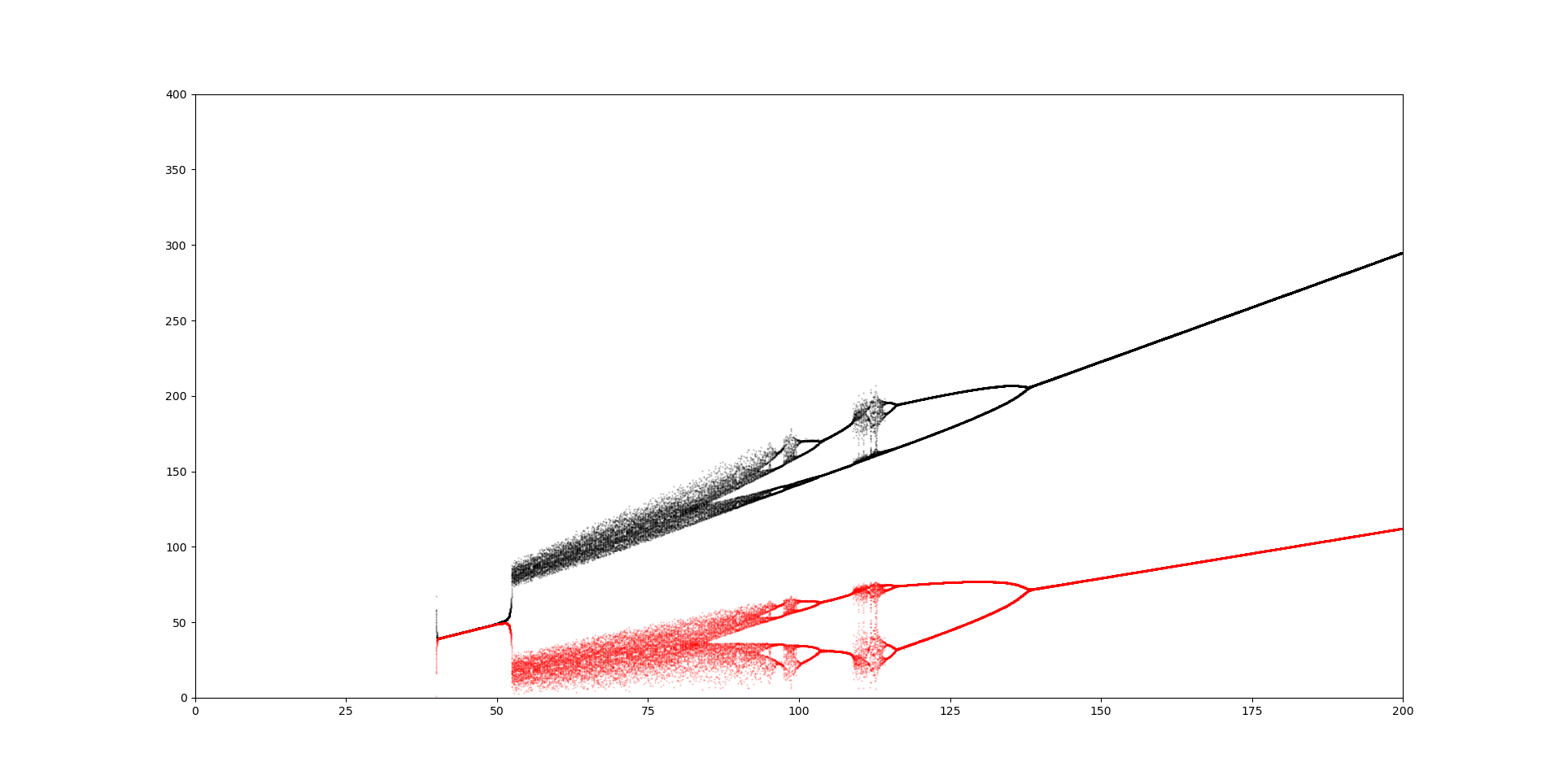
Вот способ получить похожий сюжет, используя ваш код
import numpy as np
import matplotlib.pyplot as plt
def lorenz_system(x, y, z, r, b=10, s=6):
x_dot = b * (y - x)
y_dot = r * x - y - x * z
z_dot = x * y - s * z
return x_dot, y_dot, z_dot
dr = 0.1 # parameter step size
r = np.arange(40, 200, dr) # parameter range
dt = 0.001 # time step
t = np.arange(0, 10, dt) # time range
# initialize solution arrays
xs = np.empty(len(t) + 1)
ys = np.empty(len(t) + 1)
zs = np.empty(len(t) + 1)
# initial values x0,y0,z0 for the system
xs[0], ys[0], zs[0] = (1, 1, 1)
# Save the plot points coordinates and plot the with a single call to plt.plot
# instead of plotting them one at a time, as it's much more efficient
r_maxes = []
z_maxes = []
r_mins = []
z_mins = []
for R in r:
# Print something to show everything is running
print(f"{R=:.2f}")
for i in range(len(t)):
# approximate numerical solutions to system
x_dot, y_dot, z_dot = lorenz_system(xs[i], ys[i], zs[i], R)
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# calculate and save the peak values of the z solution
for i in range(1, len(zs) - 1):
# save the local maxima
if zs[i - 1] < zs[i] and zs[i] > zs[i + 1]:
r_maxes.append(R)
z_maxes.append(zs[i])
# save the local minima
elif zs[i - 1] > zs[i] and zs[i] < zs[i + 1]:
r_mins.append(R)
z_mins.append(zs[i])
# "use final values from one run as initial conditions for the next to stay near the attractor"
xs[0], ys[0], zs[0] = xs[i], ys[i], zs[i]
plt.scatter(r_maxes, z_maxes, color="black", s=0.5, alpha=0.2)
plt.scatter(r_mins, z_mins, color="red", s=0.5, alpha=0.2)
plt.xlim(0, 200)
plt.ylim(0, 400)
plt.show()