Как подобрать кривую и определить асимптоту по данным измерений

Question

Я измерил скорость фотосинтеза при увеличивающейся интенсивности света, чтобы построить кривую PI для отдельных образцов. Я хочу определить асимптоту каждой кривой, подбирая модель к измеренным откликам для каждого образца. Ниже приводится подмножество фрейма данных, где O2_229, O2_35 и т. Д. Являются отдельными выборками.

A <- structure(list(LightIntensity = c(0, 112, 180, 272, 351, 430, 
482, 541, 609), O2_229 = c(-0.44673102313958, 0.0205958989967557, 
0.475351137678564, 0.640026082127451, 0.753504162148724, 
0.804818094545302, 0.84640533715284, 0.864374368585184, 
0.905709184251358), O2_35 = c(-0.302567249367208, 
0.181032510348939, 0.376659543810537, 0.496560233238315, 
0.540322247837853, 0.521608765794946, 0.528669387756481, 
0.516887809093099, 0.514844068198885), 
O2_230 = c(-0.542179874878379, 0.110661210104475, 
0.331450283334161, 0.568762984387555, 0.752938666550757, 
0.88143509214304, 0.945109493908027, 1.04005672006219, 
1.10246315337637), O2_36 = c(-0.510663216304597, 
0.509412237512078, 0.888867356301998, 1.18011410170533, 
1.28838854392113, 1.21645059640005, 1.29459817366225, 
1.02604605624222, 0.620845429599006), 
O2_Blank = c(-0.0291830039468955, -0.010410546520055, 
0.0414968296661793, 0.0398063330176891, -0.00945808361433628, 
-0.039882102158536, -0.0447402714742525, -0.0283811043764061, 
-0.0365212803552079)), row.names = c(NA, -9L), class = 
"data.frame")

Вот что у меня есть для сравнения моделей для одного образца (O2_229). Теперь я пытаюсь найти лучшую модель и определить асимптоту кривой каждого образца.

A <- Data_9.20
linear.model <-lm(O2_229 ~ LightIntensity, A)
summary(linear.model)
plot(A$LightIntensity, A$O2_229)
abline(lm(O2_229 ~ LightIntensity, A))

light2 <- A$LightIntensity^2
quadratic.model <-lm(O2_229 ~ LightIntensity + light2, A)
summary(quadratic.model)
lightvalues <- seq(0, 700, 100)
predictedcounts <- 
predict(quadratic.model,list(LightIntensity=lightvalues, light2 = 
lightvalues^2)) 
plot(A$LightIntensity, A$O2_229)
lines(lightvalues, predictedcounts)

Answer 1

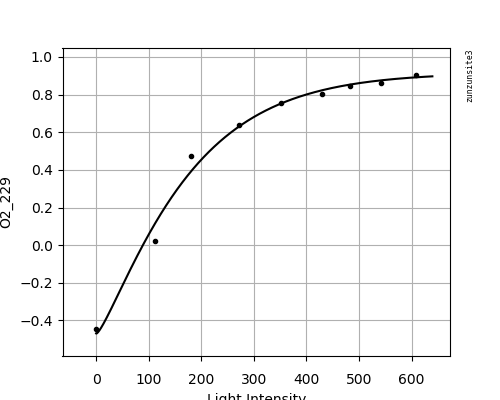
Я вижу, что вы используете квадратное уравнение для моделирования данных, которое не имеет явной асимптоты. Я обнаружил, что стандартное геометрическое уравнение со смещением "y = a * pow(x, (b*x)) + Offset" представляется хорошей моделью для данных с тем преимуществом, что параметр "Offset" является явным асимптота. Вот мои подогнанные значения для различных наборов данных (кроме O2_Blank) и графиков моделей. Я отмечаю, что набор данных 02_36, кажется, изгибается вниз, а не приближается к асимптоте.

data set O2_229:
a = -1.3851681272467806E+00
b = -1.0364478100088784E-03
Offset =  9.1626307846861987E-01

data set O2_35:
a = -8.4182899434390634E-01
b = -1.7580233358644494E-03
Offset =  5.3416172364897729E-01

data set O2_230:
a = -1.6587794258648598E+00
b = -7.2532639452267352E-04
Offset =  1.1581944009325142E+00

data set O2_36:
a = -1.6368370242440751E+00
b = -2.1647786145736897E-03
Offset =  1.1086452557429154E+00