Вычислить скорость (первую производную по времени) временного ряда

Question

Я хотел бы вычислить скорость из данных в xts Временные ряды. Мои данные выглядят так (команда ниже генерирует образец, реальные данные намного больше).

measurement <- xts(c(7.9, 8.6, 12.7, 13.3), 
                   as.POSIXct(c("2016-02-24 06:00:00",
                                "2016-02-24 07:30:00",
                                "2016-02-24 09:15:00",
                                "2016-02-24 11:15:00")))
names(measurement) <- "pos"

head(measurement)
                     pos
2016-02-24 06:00:00  7.9
2016-02-24 07:30:00  8.6
2016-02-24 09:15:00 12.7
2016-02-24 11:15:00 13.3

Если я использую diff Я получаю изменения между последовательными значениями.

diff(measurement)
                    pos
2016-02-24 06:00:00  NA
2016-02-24 07:30:00 0.7
2016-02-24 09:15:00 4.1
2016-02-24 11:15:00 0.6

Тем не менее, я хотел бы принять во внимание время и вычислить скорость (например, изменение периода времени). Я пытался использовать следующую грязную дорогу.

measurement$time  <- as.numeric(index(measurement))
measurement$speed  <- diff(measurement$pos) / diff(measurement$time) * 3600

head(measurement)
                    pos  time       speed
2016-02-24 06:00:00  7.9 1456290000        NA
2016-02-24 07:30:00  8.6 1456295400 0.4666667
2016-02-24 09:15:00 12.7 1456301700 2.3428571
2016-02-24 11:15:00 13.3 1456308900 0.3000000

Должен быть более простой и элегантный способ сделать это. Имейте в виду, что я все еще новичок в R и могу что-то упустить.

Answer 1

Я не знаю, что либо база R или xts Пакет предоставляет способ напрямую рассчитать физическую норму, как вы делаете. Немного более простой способ сделать speed расчет в часах может быть

# alternative time conversion 
  del_t <- diff(index(measurement))
  units(del_t) <- "hours"
  measurement$speed_hr <- diff(measurement$pos, na.pad=FALSE)/as.numeric(del_t)

Единицы времени, возвращаемые diff можно указать, так что в этом случае может быть установлено hours,

В более общем смысле, ваши расчеты скорости имеют разрывы в точках данных. В некоторых ситуациях также будет требоваться преемственность speed через точки данных. speed затем можно рассчитать с использованием R splinefun подпрограмма, которая может возвращать не только сплайн-интерполяцию для положения, но также и первую производную, дающую приближение скорости, которая является непрерывной и зависит от более чем двух соседних точек данных. Код может выглядеть так

# provides continuity of speed at data points
# perform cubic spline fit
  spline_fit <- splinefun(x=index(measurement), y=measurement$pos, method="natural")

# add spline speeds to measurements
  measurement$spline_spd <- spline_fit(index(measurement), deriv=1)*3600

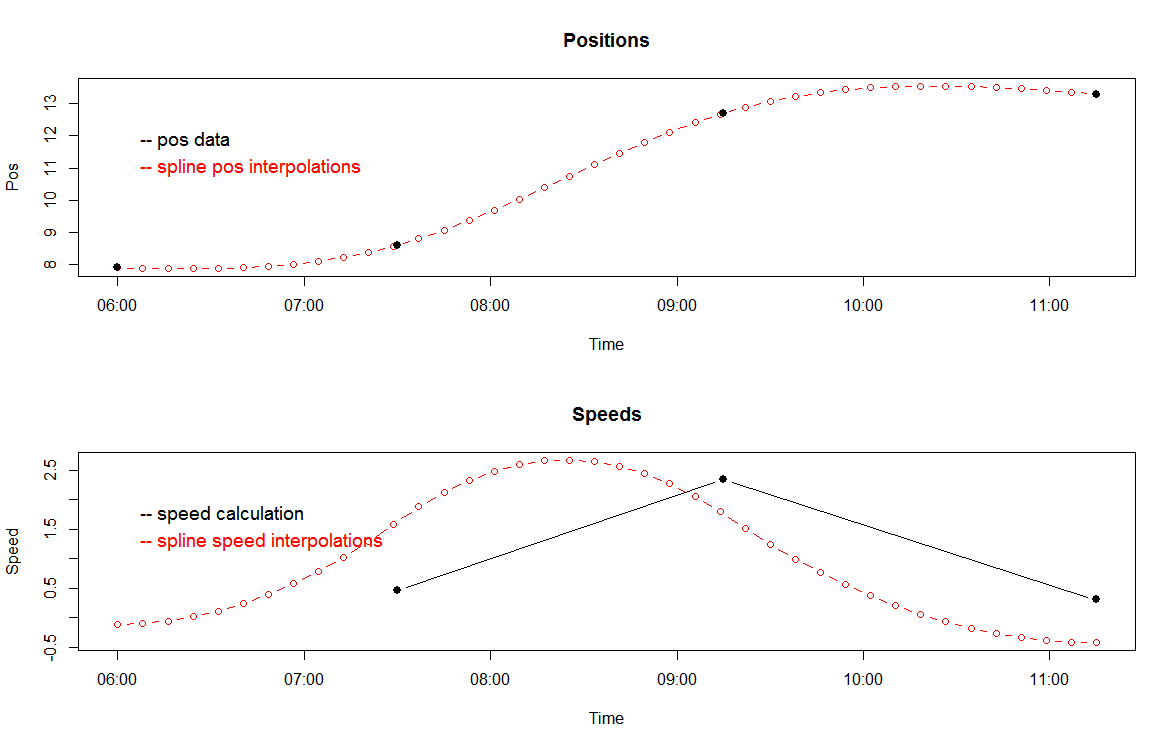
Скорости сплайна не соответствуют скоростям из первоначального расчета, но это, кажется, является результатом ограничения непрерывности в точках данных. Сюжет может помочь прояснить это.

# make a sequence of plot times for spline fits
  spline_times <- seq(start(measurement), end(measurement), length.out=40)
# plot positions
  par(mfcol=c(2,1))
  plot(spline_times, spline_fit(spline_times, deriv=0), col="red", type="b", 
       main="Positions", xlab = "Time", ylab="Pos")
  points(index(measurement), measurement$pos, type="p", pch=19, cex=1.1)
  legend("topleft", legend = c("-- pos data","-- spline pos interpolations"), 
         text.col = c("black","red"), y.intersp=.2, yjust=3., bty="n", cex=1.3)
# plot speeds
  plot(spline_times, spline_fit(spline_times, deriv=1)*3600, col="red", type="b",
       main="Speeds", xlab="Time", ylab="Speed")
  lines(index(measurement), measurement$speed, type="b", pch=19, cex=1.1)
  legend("topleft", legend = c("-- speed calculation","-- spline speed interpolations"), 
       text.col = c("black","red"), y.intersp=.2, yjust=3., bty="n", cex=1.3)

Четырех точек данных на самом деле слишком мало для хорошей подгонки сплайна, но, возможно, это передает общую идею.