Как правильно оценить в MATLAB низкую и повышенную огибающую сигнала с трендом, несколькими уровнями постоянных шагов и шумом
Я ищу надежный метод оценки низкой и верхней огибающей сигнала, состоящей из сглаженного компонента тренда, постоянных шагов между несколькими фиксированными уровнями и аддитивного шума (+ выбросы, конечно). Этот вопрос был поднят во время моей текущей исследовательской работы по обработке сигналов в реальной жизни.
Типичный пример сигнала генерируется следующим скриптом:
%% signal definition
% number of samples
Ns = 10000;
% sampling period [secs]
Ts = 1;
time = (1:Ns)*Ts;
% trend component
a = 2;
b = 0;
T = 1e4;
slope = time/Ts * 0.0005;
trend = a * sin(2*pi*time/T) + b + slope;
% steps component (4 constant levels)
step = [zeros(1,1000),linspace(0,1,6),1*ones(1,500),linspace(1,0,6),zeros(1,500),linspace(0,-2,10), -2*ones(1,1200),linspace(-2,1,15),1*ones(1,3000),linspace(1,0,6), zeros(1,3000),linspace(0,-1,6), -1*ones(1,751)];
% noise component (normal noise)
noise = 0.2*randn(1,Ns);
% noise = 0.5*(rand(1,Ns)-0.5);
%
%% show signals component
close all
figure
plot(time,trend,'r-')
hold on
plot(time,trend+step,'g-')
plot(time,trend - 2, 'b--')
plot(time,trend + 1, 'k--')
plot(time,trend+step+noise,'mo')
legend('trend','trend+steps','lowenvelope', 'upenvelope','trend+steps+noise')
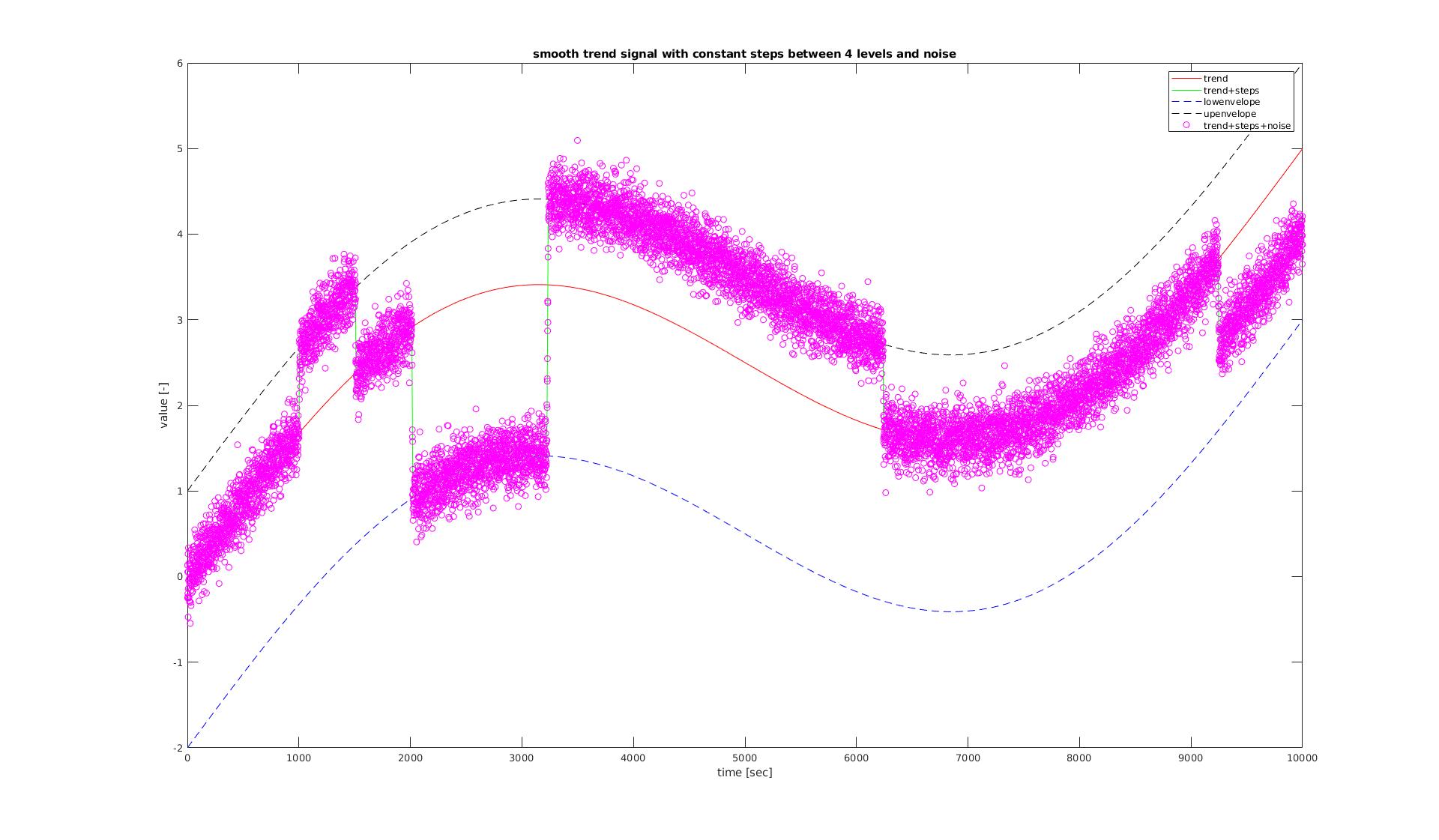
title('smooth trend signal with constant steps between 4 levels and noise')
xlabel('time [sec]')
ylabel('value [-]')
hold off
Смотрите следующее изображение
Отдельные компоненты сигнала неизвестны! Шаги всегда постоянны и находятся между небольшим количеством фиксированных уровней (обычно < 4 или 5), поэтому расчетные огибающие должны быть параллельны сигналу тренда. Шум аппроксимируется нормальным распределением с сигмой ~0,1
Есть идеи, как решить эту удивительно сложную проблему? Любые соответствующие ссылки или ссылки кода Matlab?