Создание функций распределения вероятностей (PDFs) из гистограмм

Question

Скажем, у меня есть несколько гистограмм, каждая из которых имеет счет в разных местоположениях бина (на реальной оси). например

def generate_random_histogram():

    # Random bin locations between 0 and 100
    bin_locations = np.random.rand(10,) * 100
    bin_locations.sort()

    # Random counts between 0 and 50 on those locations 
    bin_counts = np.random.randint(50, size=len(bin_locations))
    return {'loc': bin_locations, 'count':bin_counts}

# We can assume that the bin size is either pre-defined or that 
# the bin edges are on the middle-point between consecutive counts.
hists = [generate_random_histogram() for x in xrange(3)]

Как я могу нормализовать эти гистограммы, чтобы получить PDF-файлы, в которых интеграл каждого PDF-файла суммируется с единицей в заданном диапазоне (например, 0 и 100)?

Можно предположить, что гистограмма считает события на заранее заданном размере бина (например, 10)

Большинство реализаций, которые я видел, основаны, например, на гауссовых ядрах (см. scipy а также scikit-learn), которые начинаются с данных. В моем случае мне нужно сделать это по гистограммам, поскольку у меня нет доступа к исходным данным.

Обновить:

Обратите внимание, что все текущие ответы предполагают, что мы смотрим на случайную переменную, которая находится в (-Inf, +Inf). Это хорошо, как грубое приближение, но это может быть не так в зависимости от приложения, где переменная может быть определена в каком-то другом диапазоне [a,b] (например, 0 и 100 в приведенном выше случае)

Answer 1

Основным деликатесом является определение bin_edges технически они могут быть где угодно. Я выбрал среднюю точку между каждой парой бин-центров. Возможно, есть другие способы сделать это, но вот один из них:

hists = [generate_random_histogram() for x in xrange(3)]
for h in hists:
    bin_locations = h['loc']
    bin_counts = h['count']
    bin_edges = np.concatenate([[0], (bin_locations[1:] + bin_locations[:-1])/2, [100]])
    bin_widths = np.diff(bin_edges)
    bin_density = bin_counts.astype(float) / np.dot(bin_widths, bin_counts)
    h['density'] = bin_density

    data = np.repeat(bin_locations, bin_counts)
    h['kde'] = gaussian_kde(data)

    plt.step(bin_locations, bin_density, where='mid', label='normalized')
    plt.plot(np.linspace(0,100), h['kde'](np.linspace(0,100)), label='kde')

Что приведет к графику, подобному следующему (по одному для каждой гистограммы):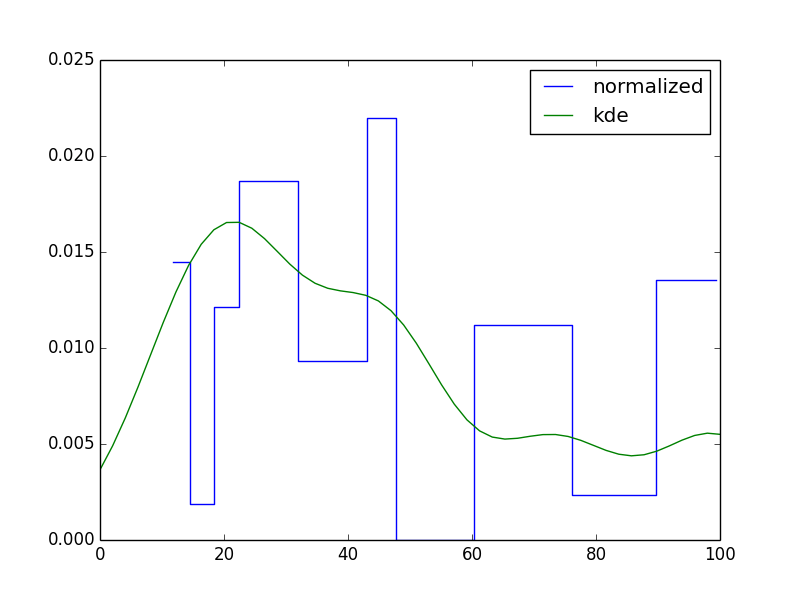

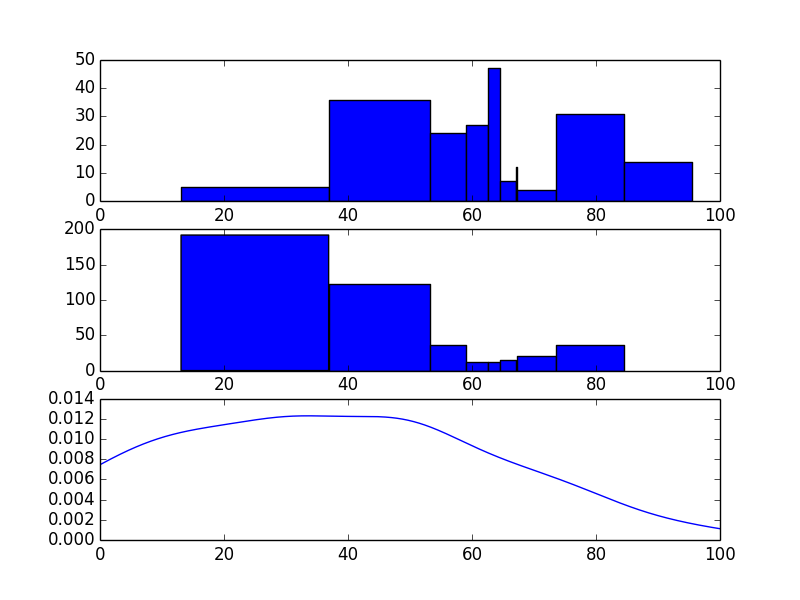
Answer 2

Здесь есть одна возможность. Я не настолько без ума от этого, но это отчасти работает. Обратите внимание, что гистограммы довольно странные, так как ширина ячейки довольно изменчива.

import numpy as np
from matplotlib import pyplot
from sklearn.mixture.gmm import GMM
from sklearn.grid_search import GridSearchCV

def generate_random_histogram():
    # Random bin locations between 0 and 100
    bin_locations = np.random.rand(10,) * 100
    bin_locations.sort()

    # Random counts on those locations
    bin_counts = np.random.randint(50, size=len(bin_locations))
    return {'loc': bin_locations, 'count':bin_counts}

def bin_widths(loc):
    widths = []
    for i in range(len(loc)-1):
        widths.append(loc[i+1] - loc[i])
    widths.append(widths[-1])
    widths = np.array(widths)
    return widths

def sample_from_hist(loc, count, size):
    n = len(loc)
    tot = np.sum(count)
    widths = bin_widths(loc)
    lowers = loc - widths
    uppers = loc + widths
    probs = count / float(tot)
    bins = np.argmax(np.random.multinomial(n=1, pvals=probs, size=(size,)),1)
    return np.random.uniform(lowers[bins], uppers[bins])

# Generate the histogram
hist = generate_random_histogram()

# Sample from the histogram
sample = sample_from_hist(hist['loc'],hist['count'],np.sum(hist['count']))

# Fit a GMM
param_grid = [{'n_components':[1,2,3,4,5]}]
def scorer(est, X, y=None):
    return np.sum(est.score(X))
grid_search = GridSearchCV(GMM(), param_grid, scoring=scorer).fit(np.reshape(sample,(len(sample),1)))
gmm = grid_search.best_estimator_

# Sample from the GMM
gmm_sample = gmm.sample(np.sum(hist['count']))

# Plot the resulting histograms and mixture distribution
fig = pyplot.figure()
ax1 = fig.add_subplot(311)
widths = bin_widths(hist['loc'])
ax1.bar(hist['loc'], hist['count'], width=widths)
ax2 = fig.add_subplot(312, sharex=ax1)
ax2.hist(gmm_sample, bins=hist['loc'])
x = np.arange(min(sample), max(sample), .1)
y = np.exp(gmm.score(x))
ax3 = fig.add_subplot(313, sharex=ax1)
ax3.plot(x, y)
pyplot.show()

Answer 3

Вот способ сделать это с помощью Pymc. Этот метод использует фиксированное количество компонентов (n_components) в модели смеси. Вы можете попробовать присоединить априор к n_components и сделать выборку поверх этого априора. Кроме того, вы можете просто выбрать что-то разумное или использовать метод поиска по сетке из моего другого ответа, чтобы оценить количество компонентов. В приведенном ниже коде я использовал 10000 итераций с записью 9000, но этого может быть недостаточно для получения хороших результатов. Я бы предложил использовать гораздо больший прожиг. Я также несколько произвольно выбрал приоры, чтобы на них можно было взглянуть. Вам придется экспериментировать с этим. Удачи вам. Вот код

import numpy as np
import pymc as mc
import scipy.stats as stats
from matplotlib import pyplot

def generate_random_histogram():
    # Random bin locations between 0 and 100
    bin_locations = np.random.rand(10,) * 100
    bin_locations.sort()

    # Random counts on those locations
    bin_counts = np.random.randint(50, size=len(bin_locations))
    return {'loc': bin_locations, 'count':bin_counts}


def bin_widths(loc):
    widths = []
    for i in range(len(loc)-1):
        widths.append(loc[i+1] - loc[i])
    widths.append(widths[-1])
    widths = np.array(widths)
    return widths


def mixer(name, weights, value=None):
    n = value.shape[0]
    def logp(value, weights):
        vals = np.zeros(shape=(n, weights.shape[1]), dtype=int)
        vals[:, value.astype(int)] = 1
        return mc.multinomial_like(x = vals, n=1, p=weights)

    def random(weights):
        return np.argmax(np.random.multinomial(n=1, pvals=weights[0,:], size=n), 1)

    result = mc.Stochastic(logp = logp,
                             doc = 'A kernel smoothing density node.',
                             name = name,
                             parents = {'weights': weights},
                             random = random,
                             trace = True,
                             value = value,
                             dtype = int,
                             observed = False,
                             cache_depth = 2,
                             plot = False,
                             verbose = 0)
    return result

def create_model(lowers, uppers, count, n_components):
    n = np.sum(count)
    lower = min(lowers)
    upper = min(uppers)
    locations = mc.Uniform(name='locations', lower=lower, upper=upper, value=np.random.uniform(lower, upper, size=n_components), observed=False)
    precisions = mc.Gamma(name='precisions', alpha=1, beta=1, value=.001*np.ones(n_components), observed=False)
    weights = mc.CompletedDirichlet('weights', mc.Dirichlet(name='weights_ind', theta=np.ones(n_components)))

    choice = mixer('choice', weights, value=np.ones(n).astype(int))

    @mc.observed
    def histogram_data(value=count, locations=locations, precisions=precisions, weights=weights):
        if hasattr(weights, 'value'):
            weights = weights.value

        lower_cdfs = sum([weights[0,i]*stats.norm.cdf(lowers, loc=locations[i], scale=np.sqrt(1.0/precisions[i])) for i in range(len(weights))])
        upper_cdfs = sum([weights[0,i]*stats.norm.cdf(uppers, loc=locations[i], scale=np.sqrt(1.0/precisions[i])) for i in range(len(weights))])

        bin_probs = upper_cdfs - lower_cdfs
        bin_probs = np.array(list(upper_cdfs - lower_cdfs) + [1.0 - np.sum(bin_probs)])
        n = np.sum(count)
        return mc.multinomial_like(x=np.array(list(count) + [0]), n=n, p=bin_probs)

    @mc.deterministic
    def location(locations=locations, choice=choice):
        return locations[choice.astype(int)]

    @mc.deterministic
    def dispersion(precisions=precisions, choice=choice):
        return precisions[choice.astype(int)]

    data_generator = mc.Normal('data', mu=location, tau=dispersion)

    return locals()

# Generate the histogram
hist = generate_random_histogram()
loc = hist['loc']
count = hist['count']
widths = bin_widths(hist['loc'])
lowers = loc - widths
uppers = loc + widths

# Create the model
model = create_model(lowers, uppers, count, 5)

# Initialize to the MAP estimate
model = mc.MAP(model)
model.fit(method ='fmin')

# Now sample with MCMC
model = mc.MCMC(model)
model.sample(iter=10000, burn=9000, thin=300)

# Plot the mu and tau traces
mc.Matplot.plot(model.trace('locations'))
pyplot.show()

# Get the samples from the fitted pdf
sample = np.ravel(model.trace('data')[:])

# Plot the original histogram, sampled histogram, and pdf
lower = min(lowers)
upper = min(uppers)
kde = stats.gaussian_kde(sample)
x = np.arange(0,100,.1)
y = kde(x)
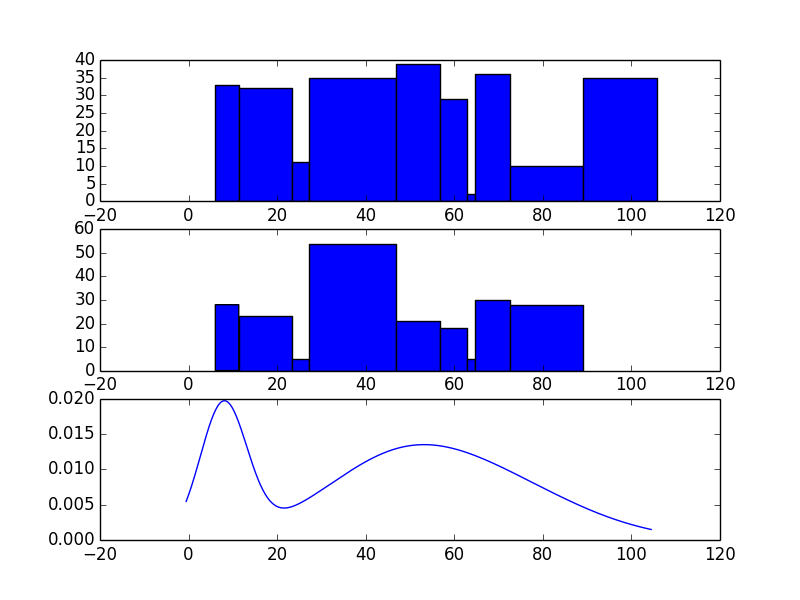
fig = pyplot.figure()
ax1 = fig.add_subplot(311)
pyplot.xlim(lower,upper)
ax1.bar(loc, count, width=widths)
ax2 = fig.add_subplot(312, sharex=ax1)
ax2.hist(sample, bins=loc)
ax3 = fig.add_subplot(313, sharex=ax1)
ax3.plot(x, y)
pyplot.show()

И, как вы можете видеть, эти два дистрибутива не выглядят одинаково. Тем не менее, гистограмма не так уж и много. Я бы поиграл с разным количеством компонентов и большим количеством итераций / прожигом, но это проект. В зависимости от ваших приоритетов, я подозреваю, что @askewchan или мой другой ответ могут вам помочь.