Имитация данных negbin из подобранной модели glmmTMB - семейство negbin1

Question

Я установил glmmTMB модель с использованием family = nbinom1. Теперь я хотел бы выполнить моделирование данных на основе прогнозируемых значений и дисперсии. Однако, судя по файлам справки, похоже, чтоrnbinom функция использует family=nbinom2 параметризация, при которой дисперсия равна mu + mu^2/size.

1) Может ли кто-нибудь помочь мне понять, как моделировать family=nbinom1 данные (где дисперсия равна mu + mu*size)?

2) Правильно ли мое извлечение / использование значения дисперсии в качестве размера?

Спасибо!

Текущий код (данные не предоставлены, потому что не имеет значения) с использованием stats:::rnbinom функция, несмотря на несоответствие определения дисперсии:

library(glmmTMB)

mod <- glmmTMB(y ~ x + (1 | ID), data = df, family = nbinom1)
preds <- predict(mod, type = "response")
size <- sigma(mod)
sim <- rnbinom(nrow(df), mu = preds, size = size)

Answer 1

Мы можем попытаться смоделировать nbinom1, поэтому, если дисперсия равна mu + mu*k:

set.seed(111)
k = 2
x = runif(100,min=1,max=3)
y = rnbinom(100,mu=exp(2*x),size=exp(2*x)/k)
ID = sample(1:2,100,replace=TRUE)
df = data.frame(x,y,ID)
mod <- glmmTMB(y ~ x + (1 | ID), data = df, family = nbinom1)

sigma(mod)
[1] 1.750076

Выше для каждого среднего, mu, я указал размер mu / k, чтобы получить ожидаемую дисперсию mu*k. Это показывает, что если вы правильно параметризуете rnbinom, вы вернетесь к rnbinom1.

Теперь с этой моделью, если нам нужно моделировать данные, она просто использует ту же параметризацию, что и выше:

preds <- predict(mod, type = "response")
size <- sigma(mod)
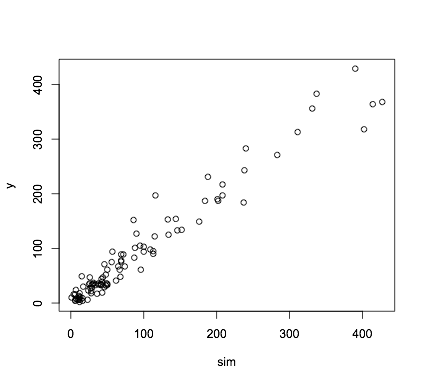
sim <- rnbinom(nrow(df), mu = preds, size = preds/size)

plot(sim,df$y)

Answer 2

Здесь есть множество проблем, в том числе:

• sigma(mod)дает оценочное стандартное отклонение остатков; это не дисперсия, а квадратный корень из дисперсии, поэтому вы можете возвести его в квадрат.
• существует множество параметризаций отрицательного биномиального распределения помимо версии R, но в версии R, если среднее значение mean(dat) и дисперсия var(dat) тогда вы можете оценить size с mean(dat)^2/(var(dat)-mean(dat)) и вероятность prob с mean(dat)/var(dat)
• rnbinom() будет терпеть sizeбыть нецелым или бесконечным, несмотря на то, что это теоретическая чепуха; это не потерпитsize быть отрицательным, что может произойти, если var(dat) меньше чем mean(dat). Также будут проблемы, среднее отрицательное или еслиsize равно нулю.

Так что, возможно, вы могли бы подумать об адаптации линий моделирования к чему-то вроде

sizes <- ifelse(sigma(mod) ^ 2 > preds, preds ^ 2 / (sigma(mod) ^ 2 - preds), Inf)
sim <- ifelse(preds > 0, rnbinom(nrow(df), mu = preds, size = sizes), 0) 

тогда вы все равно можете получать ошибки, когда sigma(mod) меньше или равно preds