Изменение высоты импортируемого сигнала логарифмически / экспоненциально с течением времени
Как я могу изменить высоту импортированного сигнала логарифмически / экспоненциально с течением времени?
Обратите внимание, что импортируемые сигналы, которые будут использоваться, не являются одночастотными, поэтому простая развертка или команда чирпа не будут работать, так как я буду импортировать вокальные аудиофайлы, я просто создал приведенные ниже примеры, чтобы они работали и могли быть протестированы / показаны проблемы у меня возникли.
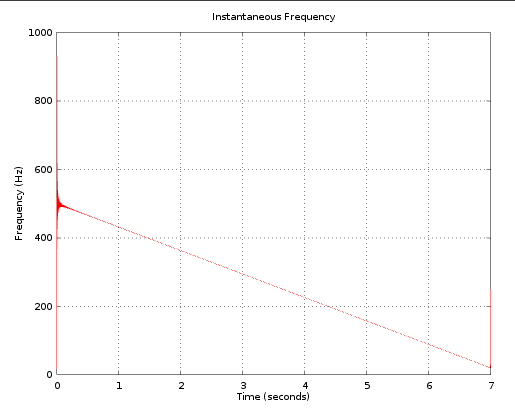
Я могу линейно изменять высоту сигнала во времени, что прекрасно работает, см. Часть 1 тестового кода и частотный график ниже. Спасибо Шелджону за код
%Sweep question part 1
clear all,clf reset,tic,clc
pkg load signal %load packages
%%%----create signal
start_freq=500;
end_freq=20;
fs=22050
len_of_sig=7; %in seconds
t=linspace(0,2*pi*len_of_sig,fs*len_of_sig);
orig_sig1=.8*sin(start_freq*t);
wavwrite([orig_sig1(:)] ,fs,16,strcat('/tmp/0_sig.wav')); % export file
%%%---import signal
[ya, fs, nbitsraw] = wavread('/tmp/0_sig.wav');
orig_total_samples=length(ya); %make this the same length as signal wave
t_import=linspace(0,2*pi*(orig_total_samples/fs),orig_total_samples);
%%%%----Begin linsweep
x = ya(:);
fac=(end_freq-start_freq)/length(x); %linear slope
n = numel(x); % number of timepoints
m = mean(x); % average of the signal
k = transpose(0:n-1); %
h = hilbert( x - m ); % analytic signal
env1 = abs(h); % envelope
sweep=fac*pi*k.^2/(fs); %linearly increasing offset original %alter curve here
p = angle(h) + sweep; % phase + linearly increasing offset original
y = m - imag(hilbert( env1 .* sin(p) )); % inverse-transform
wavwrite([y(:)] ,fs,16,strcat('/tmp/0_sweep.wav')); % export file
%%%----------Used for plotting
z = hilbert(y);
instfreq = fs/(2*pi)*diff(unwrap(angle(z))); %orginal
t_new=t_import/(2*pi); %converts it to seconds
plot(t_new(2:end),instfreq,'-r')
xlabel('Time (secnds)')
ylabel('Frequency (Hz)')
grid on
title('Instantaneous Frequency')
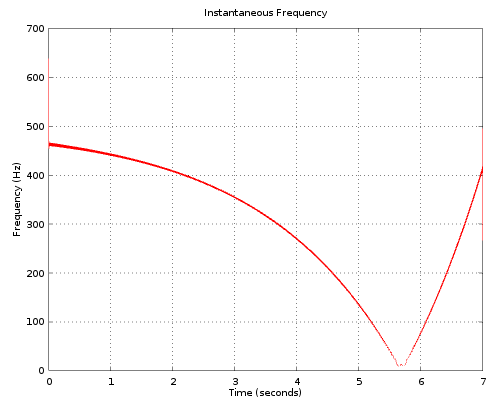
Проблемы с кодом, который я имею ниже:
1) Частота не начинается и не заканчивается на правильной частоте.
2) не имеет правильных склонов
Я считаю, что это связано с переменными fac и sweep. Я просто не уверен, как правильно их вычислить.
fac=log(start_freq/end_freq)/length(x); %slope
sweep=-(start_freq)*exp(fac*k); %alter curve here
-
%-----------------Sweep question part 2
clear all,clf reset,tic,clc
pkg load signal %load packages
%%%----create signal
start_freq=500;
end_freq=20;
fs=22050
len_of_sig=7; %in seconds
t=linspace(0,2*pi*len_of_sig,fs*len_of_sig);
orig_sig1=.8*sin(start_freq*t);
wavwrite([orig_sig1(:)] ,fs,16,strcat('/tmp/0_sig.wav')); % export file
%%%---import signal
[ya, fs, nbitsraw] = wavread('/tmp/0_sig.wav');
orig_total_samples=length(ya); %make this the same length as signal wave
t_import=linspace(0,2*pi*(orig_total_samples/fs),orig_total_samples);
%%%%----Begin linsweep
x = ya(:);
fac=log(start_freq/end_freq)/length(x); %slope
n = numel(x); % number of timepoints
m = mean(x); % average of the signal
k = transpose(0:n-1); %
h = hilbert( x - m ); % analytic signal
env1 = abs(h); % envelope
sweep=-(start_freq)*exp(fac*k); %alter curve here
p = angle(h) + sweep; % phase + increasing offset
y = m - imag(hilbert( env1 .* sin(p) )); % inverse-transform
wavwrite([y(:)] ,fs,16,strcat('/tmp/0_sweep.wav')); % export file
%%%----------Used for plotting
z = hilbert(y);
instfreq = fs/(2*pi)*diff(unwrap(angle(z))); %orginal
t_new=t_import/(2*pi); %converts it to seconds
plot(t_new(2:end),instfreq,'-r')
xlabel('Time (seconds)')
ylabel('Frequency (Hz)')
grid on
title('Instantaneous Frequency')
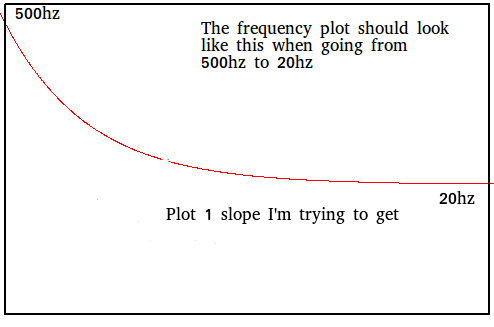
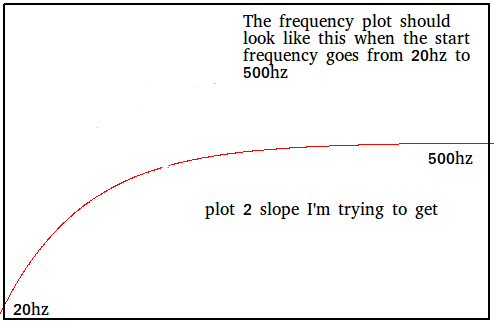
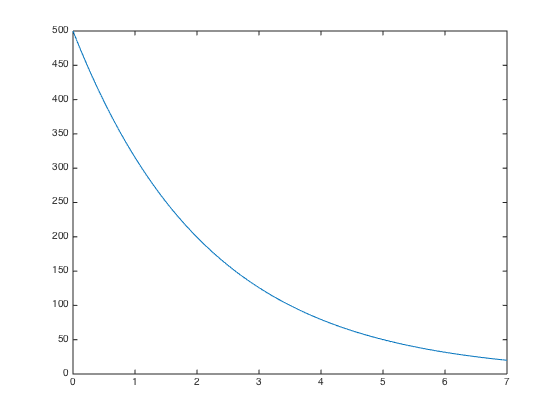
Уклоны, которые я пытаюсь получить, это когда начальная частота начинается с 500 Гц и достигает 20 Гц. И когда начальная частота начинается с 20 Гц и достигает 500 Гц. См. Графики ниже: Примечание. Эти частоты будут меняться, поэтому я пытаюсь получить правильную формулу / уравнение, которое будет вычислять эти наклоны при необходимости.
PS: я использую Octave 4.0, которая похожа на Matlab.
Обратите внимание, что импортируемые сигналы, которые будут использоваться, не являются одночастотными, поэтому простая развертка или команда чирпа не будут работать, так как я буду импортировать вокальные аудиофайлы, я просто создал приведенные ниже примеры, чтобы они работали и могли быть протестированы / показаны проблемы у меня возникли.
1 ответ
Я могу сделать так, чтобы сюжет выглядел как интересующий вас сюжет, внеся следующие изменения в ваш код. Некоторые из них просто косметические для меня (например, мне нравится, чтобы мои переменные времени оставались в единицах секунд).
Соответствующие изменения:
От:
t=linspace(0,2*pi*len_of_sig,fs*len_of_sig);
orig_sig1=.8*sin(start_freq*t);
fac=log(start_freq/end_freq)/length(x); %slope
Для того, чтобы:
t=linspace(0,len_of_sig,fs*len_of_sig);
orig_sig1=0.8*sin(start_freq*t*2*pi);
fac=log(end_freq/start_freq)/length(x);
sweep=(start_freq*2*pi/fs)*exp(fac*k); %alter curve here
Вот некоторые другие изменения, которые я сделал,
y = env1.*sin(p);
% and later for consistency
t_import=linspace(0,orig_total_samples/fs,orig_total_samples);
t_new=t_import; %t is seconds
facНа мой взгляд, будет разница с вашим началом и концом, так что это будет: log(endFreq)-log(startFreq) или же log(endFreq/startFreq) с дополнительной нормализацией по длине. Это может быть отражено с отрицательным знаком впереди.
Одна проблема с разверткой может произойти, когда вы используете его для расчета p=angle(h)+sweep; где angle(h) в радианах.
Проблема радиан в единицах Гц может быть причиной некоторых трудностей.