Расчет расстояния по шестиугольной сетке
Я пытаюсь найти, сколько шестиугольников находится между двумя точками на гекс-сетке. Я попытался найти формулу в Интернете, но мне не удалось найти форму, которая соответствует типу шестнадцатеричной сетки, которую я использую.
Шестнадцатеричная сетка выложена так же, как эта с той же системой координат: http://www.gamedev.net/index.php?app=core&module=attach§ion=attach&attach_rel_module=ccs&attach_id=1962
Я знаю, что это может быть невозможно с этой системой координат, но это последнее усилие, прежде чем я вернусь и изменю его. Заранее большое спасибо.
11 ответов
Спасибо @user2709663 и @jonathankoren за ответы. Я провожу много времени с вашими ответами, но обнаружил, что у обоих есть некоторые проблемы. Или, по крайней мере, тип сетки, рассматриваемый для этих ответов, не указан четко. Тем не менее, я нашел очень хороший учебник и код реализации этой проблемы, а также библиотеку для управления шестигранной сеткой по адресу: http://www.redblobgames.com/grids/hexagons/ (код библиотеки: http://www.redblobgames.com/grids/hexagons/implementation.html). Я также реализую версию кода расстояния Matlab для вертикальной разметки "odd-q" следующим образом:
function f = offset_distance(x1,y1,x2,y2)
ac = offset_to_cube(x1,y1);
bc = offset_to_cube(x2,y2);
f = cube_distance(ac, bc);
end
function f = offset_to_cube(row,col)
%x = col - (row - (row&1)) / 2;
x = col - (row - mod(row,2)) / 2;
z = row;
y = -x-z;
f = [x,z,y];
end
function f= cube_distance(p1,p2)
a = abs( p1(1,1) - p2(1,1));
b = abs( p1(1,2) - p2(1,2));
c = abs( p1(1,3) - p2(1,3));
f = max([a,b,c]);
end
Вот код тестирования Matlab
sx = 6;
sy = 1;
for i = 0:7
for j = 0:5
k = offset_distance(sx,sy,i,j);
disp(['(',num2str(sx),',',num2str(sy),')->(',num2str(i),',',num2str(j),')=',num2str(k)])
end
end
Если бы вы использовали систему координат, которая проходит вдоль гексагон в двух направлениях, вы могли бы использовать:
distance = max(
abs(dest.y - start.y),
abs(dest.x - start.x),
abs((dest.x - dest.y)*-1 - (start.x - start.y)*-1)
)
Однако вы этого не сделали, вы используете волнистую систему координат, которая идет с зерном только в одном направлении (горизонтальном). К счастью, мы можем преобразовать между двумя, используя
straight.y = squiggle.y
straight.x = ciel(squiggle.y / -2) + squiggle.x
Итак, решение для расстояния с использованием этой системы уравнений дает вам:
distance = max(
abs(dest.y - start.y),
abs(ceil(dest.y / -2) + dest.x - ceil(start.y / -2) - start.x),
abs(-dest.y - ceil(dest.y / -2) - dest.x + start.y + ceil(start.y / -2) + start.x)
)
Это даст вам манхэттенское расстояние между двумя гексами, используя только их координаты (при условии, что я не сделал никаких опечаток, транспонирующих x и y, так как ваша сетка повернута на 90 градусов от моей). Однако вы должны купить печенье для моего учителя алгебры средней школы, чтобы оно работало, иначе я испорчу дистрибутивную собственность.
Примечание: может потребоваться возиться с отрицательными координатами, я не проверял.
Принятый ответ неверен. Сначала я с подозрением относился к этому, когда упомянул об использовании ортогональных координат на неортогональных осях, но выполнение кода по моему собственному решению показывает, что переоценка расстояния усложняется.
Фактическое правильное решение:
def hexDistance(start, dest):
if (start.x == dest.x):
return abs(dest.y - start.y)
elif (start.y == dest.y):
return abs(dest.x - start.x)
else:
dx = abs(dest.x - start.x)
dy = abs(dest.y - start.y)
if start.y < dest.y:
return dx + dy - int(math.ceil(dx / 2.0))
else:
return dx + dy - int(math.floor(dx / 2.0))
Это использует hex-> квадратное представление:
------
------ 0, +1 ------
-1, +1 ------ +1, +1
------ 0, 0 ------
-1, 0 ------ +1, 0
------ 0, -1 ------
------
--------------------------
| -1, +1 | 0, +1 | +1, +1 |
| --------------------------
| -1, 0 | 0, 0 | +1, 0 |
| -------------------------- |
| | 0, -1 | |
--------------------------
Чтобы найти кратчайший путь между двумя гексами:
- Начиная с одного гекса,
- Находясь в разных рядах, следуйте по диагонали к другому ряду.
- Находясь в том же ряду, идите прямо в другой гекс.
Давайте назовем разницу в направлении х dx и разница в направлении у dy, Если dy / 2 > dx, вам не нужно делать второй шаг, поэтому расстояние просто dy, В противном случае расстояние dy + (dx - dy / 2), Если я не ошибся.
M H Rasel связал этот пост в своем предыдущем ответе: Hexagonal Grids. После этого отличного поста я понял, что мне нужны координаты куба; это дает самый простой способ рассчитать расстояния. Вот фрагмент кода в Котлине:
data class Point(val x: Int, val y: Int, val z: Int) {
fun distance(b: Point): Int {
return (abs(x - b.x) + abs(y - b.y) + abs(z - b.z)) / 2
}
}
var x = 0
var y = 0
var z = 0
val p1 = Point(x, y, z) // starting position
val steps = "ne,ne,ne".split(",") // go to North-East 3 times
for (direction in steps) {
when(direction) {
"n" -> { ++y; --z }
"ne" -> { ++x; --z }
"se" -> { ++x; --y }
"s" -> { --y; ++z }
"sw" -> { --x; ++z }
"nw" -> { ++y; --x }
}
}
val p2 = Point(x, y, z) // we arrived here
val dist = p1.distance(p2) // the result is here (in this example: 3)
Редактировать: я предполагаю плоскую шестигранную сетку.
Если у вашего гексагонального тайлинга есть направления: N, NE, SE, S, SW, NW, как в задаче Advent of Code 2017, и вы смещаете цель на (0,0) (заранее вычитая свою позицию из цели), следующее логика у меня сработала
def distance(self):
# Take diagonal steps towards self.x == 0
steps = abs(self.x)
# y moves closer to 0 by steps because moving diagonal, but never moving too far
if self.y > 0:
# Might still be positive, but never negative
y = max(self.y - steps, 0)
else:
# Might still be negative, but not positive
y = min(self.y + steps, 0)
# You move 2 positions north/south by a single move so divide y's by 2
return abs(y) // 2 + abs(steps)
Я думаю, что это может работать для гексагональной сетки с направлениями EAST и WEST вместо NORTH и SOUTH, как у вас, просто переключая роли x и y. В этом случае вы должны двигаться к self.y == 0 по диагонали (при необходимости) и т. Д.
Вот ответ для координат С# и Offset "even-r". Сначала проверьте эту арктайл: https://www.redblobgames.com/grids/hexagons/
static int distanceBetweenCells(int x1, int y1, int x2, int y2)
{
Vector3 evenr_to_cube(int row, int col)
{
int q = col - ((row + (row % 2))/2);
int r = row;
return new Vector3(q, r, -q - r);
}
Vector3 point_1 = evenr_to_cube(x1, y1);
Vector3 point_2 = evenr_to_cube(x2, y2);
int a = (int)Math.Abs(point_1.X - point_2.X);
int b = (int)Math.Abs(point_1.Y - point_2.Y);
int c = (int)Math.Abs(point_1.Z - point_2.Z);
return Math.Max(a, Math.Max(b, c));
}
Вы можете легко изменить это для своего типа координат, используя статью выше.
Вот метод прямого расчета, основанный на четырех преобразованиях, которые отображают все входные данные в область между положительным вектором y и вектором под углом 30 градусов. Сначала рассмотрим плоские шестиугольники по оси Y. Ось x будет волнистой.
- Переведите первую координату в 0,0
- Сложите левую половину на правую половину, сохраняя ось Y
- Согните область между нисходящим вектором 30 градусов и осью y на область между осью y и направленным вверх 30-градусным вектором. Направленный вниз 30-градусный вектор будет отображен на направленный вверх 30-градусный вектор.
- Согните область под углом 30 градусов вверх к области между осью Y и вектором угла 30 градусов вверх.
После всего этого кратчайший путь лежит вверх на 30 градусов до цели x и прямо вверх до цели y.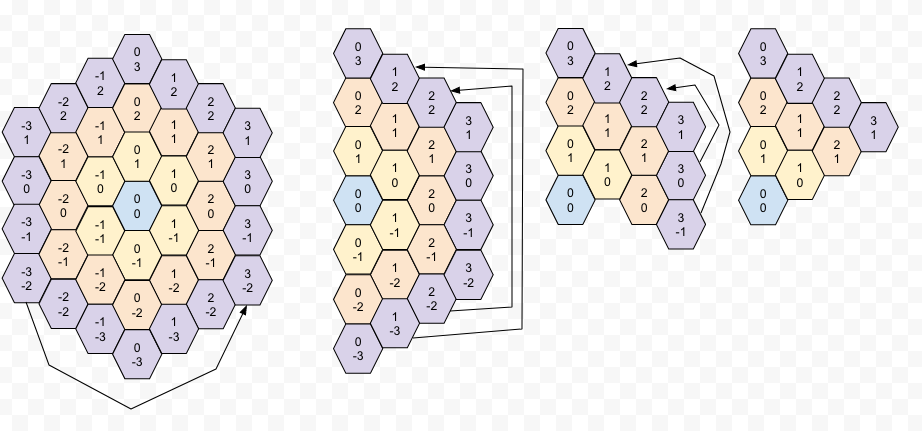
def range x1, y1, x2, y2
# translate x1,y1 to origin and
# and fold left half over right side
rx = (x2 - x1).abs
ry = y2 - y1 - (rx % 2) * (x1 % 2)
# fold along 30deg downward
if ry <= -rx / 2
ry = ry.abs - rx % 2
# rx remains unchanged
else
# fold along 30deg upward
if ry < rx / 2
c = rx / 2 - ry # steps down from 30deg line
ry = rx / 2 + (c + (rx % 2)) / 2
rx -= c # rx update must be after ry
end
end
rx + ry - rx / 2
end
Вот субоптимальный, но не слишком субоптимальный (должен быть O(n)) алгоритм:
Сначала создайте функцию, которая определяет, пересекает ли шестиугольник в определенном месте в шестигранной сетке отрезок линии с определенной начальной и конечной точкой (например, рассчитайте шесть линий, из которых он состоит, и сделайте что-то вроде: http://alienryderflex.com/intersect/.)
Во-вторых, создайте функцию, которая определяет, в каком шестиугольнике на шестигранной сетке находится точка.
Теперь напишите свой алгоритм так:
- Держите список всех шестиугольников, которые пока перекрывают отрезок
- Начните с шестиугольника, в котором находится начало отрезка
- Для каждого шестиугольника, окружающего последний перекрывающийся, если его нет в списке, посмотрите, пересекает ли lin segmente этот шестиугольник. Если так, сделайте это новым заголовком списка и повторите
- Если у нас закончились шестиугольники, вернем список, который мы сделали
Я бы посоветовал вам протестировать случай, когда отрезок прямой будет точно параллелен и проходит вдоль шва между шестиугольниками, чтобы увидеть, получаете ли вы шестиугольники с одной стороны, с обеих сторон или ни с одной (и, таким образом, останавливаете).
Изображение, объясняющее систему координат
поэтому, к сожалению, я не знаю, какую систему координат вы использовали тогда, потому что ссылка больше не работает, но большинство решений, размещенных здесь, не сработали для меня. Это система координат, которую я использовал:
------
------ 0, +1 ------
-1, +1 ------ +1, 0
------ 0, 0 ------
-1, 0 ------ +1, -1
------ 0, -1 ------
------
--------------------------
| -1, +1 | 0, +1 | |
|--------------------------|
| -1, 0 | 0, 0 | +1, 0 |
|--------------------------|
| | 0, -1 | +1, -1 |
--------------------------
И это код/формула, которая работала у меня для точек (x1,y1) и (x2,y2):
public int distance(int x1, int y1, int x2, int y2){ //distance of hexfields, 1 is source 2 is target
int dx = Mathf.Abs(x1 - x2);
int dy = Mathf.Abs(y1 - y2);
if(dx == 0){ return dy; }
else if(dy == 0){ return dx; }
else{
if(x2 < x1 && y2 < y1){ //empty Corner
return dx+dy;
}else if(x2 < x1 && y2 > y1){ //Filled Corner
return Mathf.Max(dx, dy);
}else if(x2 > x1 && y2 < y1){ //Filled Corner
return Mathf.Max(dx, dy);
}else if(x2 > x1 && y2 > y1){ //empty Corner
return dx+dy;
}else return 0;
}
}
Это, конечно, можно было бы оптимизировать с точки зрения качества кода, но его было бы легче понять, как сейчас.
Если плитки на сетке потенциально могут быть заблокированы, то вас интересует алгоритм решения лабиринтов A* (или A-Star): http://labs.makemachine.net/2010/03/a-star-maze-solver/
Механизм, использованный в этом видео, применяется к сетке квадратов, но при отсутствии какого-либо дополнительного кодирования его можно применить к шестиугольной сетке. Для каждой плитки решатель знает, какие плитки использовать дальше, потому что плитки хранят указатели на окружающие плитки. В сетке квадратов каждая ячейка будет хранить максимум 4 указателя (максимум, потому что они хранят только указатели на незаблокированные ячейки), и единственное отличие в вашем случае будет хранить максимум 6 указателей.
Если плитки всегда проходимы, то A * наверняка выполнит свою работу, однако, вероятно, есть более быстрый путь. Если я правильно истолковываю ваш вопрос, вас интересует не расстояние, а подсчет целых чисел числа гексов между двумя заданными гексами? Попробуйте следующее:
class Coord {
int x;
int y;
}
int dist(Coord hex1, Coord hex2) {
int xSteps = Math.abs(hex1.x - hex2.x);
int ySteps = Math.abs(hex1.y - hex2.y);
return Math.max(xSteps, ySteps) + Math.abs(xSteps - ySteps);
}
Почему вы можете спросить? Этот вопрос касается определения того, сколько раз мы должны двигаться вертикально или горизонтально, а не по диагонали. Мы хотим двигаться по диагонали настолько, насколько это возможно, иначе мы не будем умно относиться к нашим расстояниям. Math.abs(xSteps - ySteps) это число недиагональных ходов, которые мы должны сделать. Добавьте к этому большее из расстояний x и y, и все готово.