Поверните геометрию так, чтобы ее плоскость соответствовала базовой плоскости

Question

У меня есть трехмерная кристаллическая структура, записанная в декартовых координатах. Уточняю фрезеровку кристалла. Затем эта плоскость Миллера должна выровняться с плоскостью xy системы отсчета.

Более ранняя ветка помогла мне добиться этого. Были предприняты следующие шаги:

• Определить мельник-самолет
• Создайте локальную декартову систему отсчета, ориентированную на плоскость Миллера
• Получите единичные векторы этого локального кадра
• Возьмите продукт этих единичных векторов с векторами, которые описывают положение атома по сравнению с исходной точкой отсчета.

Указание таких плоскостей Миллера, как (1 0 0), (0 -2 1), (10, 0 1), не проблема и отлично работает. Однако задание плоскости Миллера как (1 1 1) приводит к перекосу кристалла.

Я включил здесь изображение для иллюстрации.

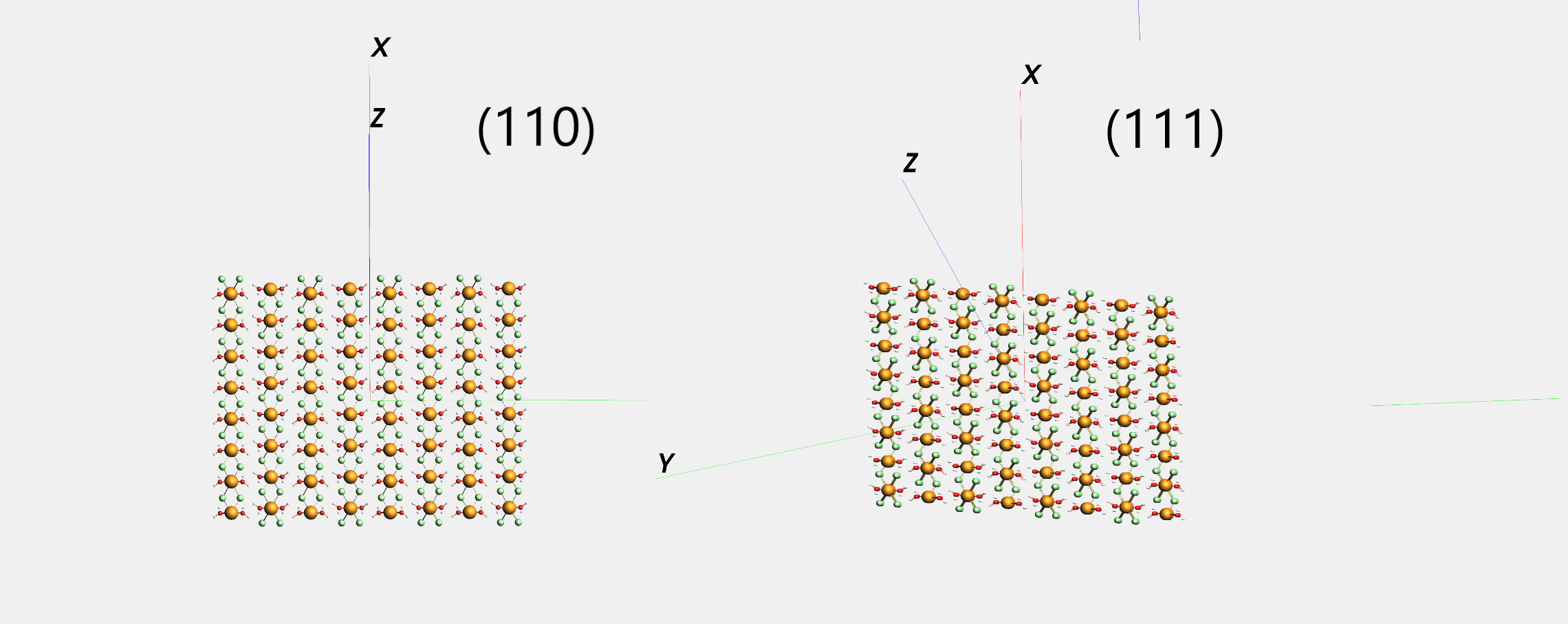
Здесь приведен фрагмент кода, использованный для этой операции. Вызывается MillerRotate. Он возвращает единичные векторы, которые будут использоваться для продукта с векторами координат атомов. Этот inproduct взят в классе Rotate.

class MillerRotate(Rotate):
def __init__(self, indices):
    self.indices = indices

def rotate_func(self, geom):
    data = geom.coordinates
    lattice = np.array([ geom.lattice[0][0], geom.lattice[1][1], geom.lattice[2][2] ])

    if (self.indices == [0,0,0]):
        raise Exception(
                "Cannot rotate 0 0 0")

    # get 3 points at the miller plane    
    a = np.zeros((len(lattice), len(lattice)))
    for i in range(len(lattice)):
        if (self.indices[i] != 0):
            a[i][i] = self.indices[i]*lattice[i]
        else:
            a[i][i] = lattice[i]
            j = self.indices.index(next(filter(lambda x: x!=0, self.indices)))
            a[i][j] = self.indices[j]*lattice[j]

    # compute two vectors to get plane 
    v1 = a[1]-a[0]
    v2 = a[2]-a[0]

    # compute unit vectors
    z = np.cross(v1,v2)
    y = np.cross(v1,z)
    x = np.cross(y ,z)
    z = z/max(z,key=abs)
    y = y/max(y,key=abs)
    x = x/max(x,key=abs)

    # matrix to be taken as inproduct with atom coordinates.
    A = np.array([x, y, z])

    if np.linalg.det(A) < 0.0:
        A[2,:] *= -1.0

    return A

class Rotate(Operation):
'''Generic rotation'''
def __init__(self):
    self.rotate_func = None

def __call__(self, geom):
    data = geom.coordinates
    A = self.rotate_func(geom)
    detA = np.linalg.det(A)
    if detA < 0.0:
        raise Exception("Determinant of Rotation needs to be 1")
    tmp = np.dot(data, A.T)
    data[:] = tmp[:]