Правильный способ подачи данных временных рядов в LSTM с отслеживанием состояния?
Предположим, у меня есть последовательность целых чисел:
0,1,2, ..
и хотите предсказать следующее целое число по последним 3 целым числам, например:
[0,1,2]->5, [3,4,5]->6, так далее
Предположим, я настроил свою модель так:
batch_size=1
time_steps=3
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, time_steps, 1), stateful=True))
model.add(Dense(1))
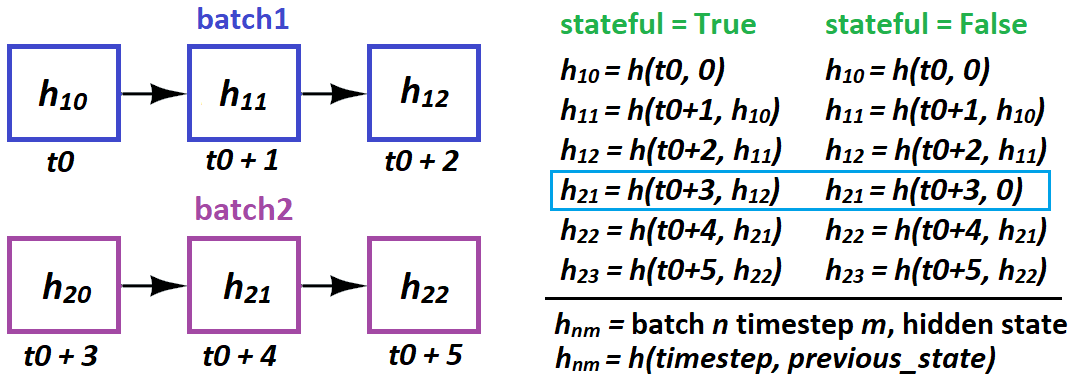
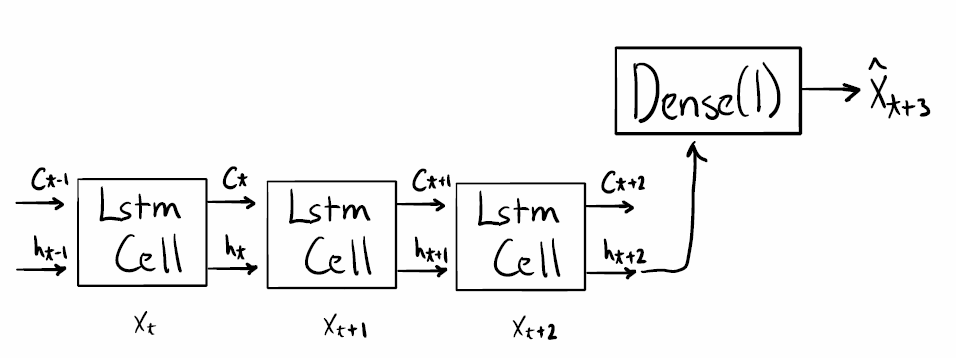
Насколько я понимаю, эта модель имеет следующую структуру (извините за грубый рисунок):
Первый вопрос: правильно ли я понимаю?
Обратите внимание, я нарисовал предыдущие состояния C_{t-1}, h_{t-1} ввод изображения, как это показано при указании stateful=True. В этой простой задаче "прогнозирование следующего целого числа" производительность должна улучшиться за счет предоставления этой дополнительной информации (если предыдущее состояние является результатом трех предыдущих целых чисел).
Это подводит меня к моему основному вопросу: кажется, стандартной практикой (например, см. Этот пост в блоге и утилиту предварительной обработки keras TimeseriesGenerator) является подача в модель ступенчатого набора входных данных во время обучения.
Например:
batch0: [[0, 1, 2]]
batch1: [[1, 2, 3]]
batch2: [[2, 3, 4]]
etc
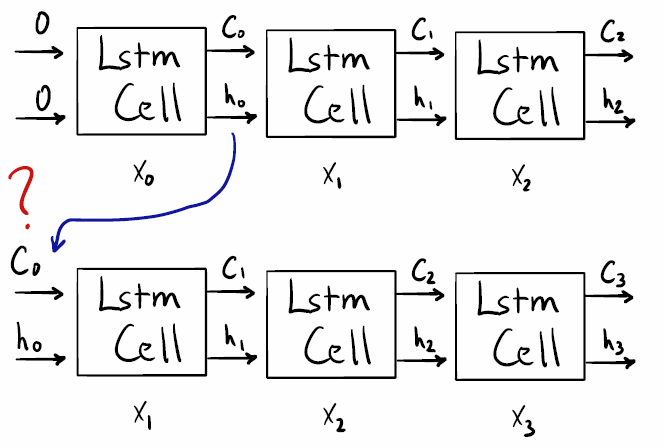
Это меня смутило, потому что кажется, что для этого требуется вывод 1-й ячейки Lstm (соответствует 1-му временному шагу). Смотрите этот рисунок:
Из документов tensorflow:
Stateful: Boolean (по умолчанию False). Если True, последнее состояние для каждой выборки с индексом i в пакете будет использоваться в качестве начального состояния для выборки с индексом i в следующем пакете.
кажется, что это "внутреннее" состояние недоступно, и все, что доступно, - это конечное состояние. Смотрите этот рисунок:
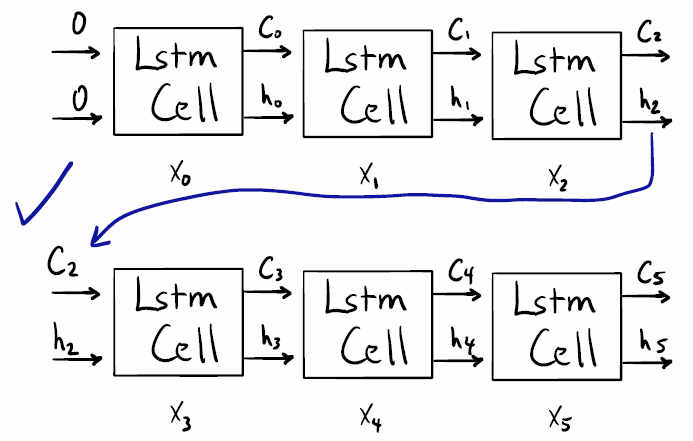
Итак, если я правильно понимаю (а это явно не так), не следует ли нам подавать неперекрывающиеся окна образцов в модель при использовании stateful=True? Например:
batch0: [[0, 1, 2]]
batch1: [[3, 4, 5]]
batch2: [[6, 7, 8]]
etc
1 ответ
Ответ: зависит от решаемой проблемы. В вашем случае одноэтапного прогнозирования - да, можно, но не обязательно. Но независимо от того, сделаете вы это или нет, это существенно повлияет на обучение.
Пакетный или образец механизма ("см. AI" = см. Раздел "дополнительная информация")
Все модели рассматривают образцы как независимые примеры; Пакет из 32 образцов похож на подачу по 1 образцу за раз, 32 раза (с отличиями - см. AI). С точки зрения модели, данные разделяются на пакетное измерение,batch_shape[0], и размеры элементов, batch_shape[1:]- двое "не разговаривают". Единственная связь между ними - через градиент (см. AI).
Партии с перекрытием и без перекрытия
Возможно, лучший способ понять это - основанный на информации. Я начну с двоичной классификации таймсерий, а затем свяжу ее с предсказанием: предположим, у вас есть 10-минутные записи ЭЭГ, 240000 временных шагов каждая. Задача: захват или невыход?
- Поскольку 240k - это слишком много для RNN, мы используем CNN для уменьшения размерности.
- У нас есть возможность использовать "скользящие окна" - т.е. кормить подсегмент за раз; давайте использовать 54k
Возьмите 10 образцов, сформируйте (240000, 1). Как кормить?
(10, 54000, 1), включены все образцы, нарезка какsample[0:54000]; sample[54000:108000]...(10, 54000, 1), включены все образцы, нарезка какsample[0:54000]; sample[1:54001]...
Что из двух вышеперечисленных вы выберете? Если (2), ваша нейронная сеть никогда не перепутает припадок с неприпадом для этих 10 образцов. Но он также ничего не знает о любом другом образце. То есть, он будет сильно переобучен, потому что информация, которую он видит за итерацию, почти не отличается (1/54000 = 0,0019%) - так что вы в основном скармливаете ему одну и ту же партию несколько раз подряд. Теперь предположим (3):
(10, 54000, 1), включены все образцы, нарезка какsample[0:54000]; sample[24000:81000]...
Намного разумнее; теперь наши окна перекрываются на 50%, а не на 99,998%.
Прогноз: плохое перекрытие?
Если вы делаете одноэтапный прогноз, теперь информационный ландшафт изменится:
- Скорее всего, длина вашей последовательности составляет faaar от 240000, поэтому перекрытия любого рода не страдают от эффекта "одна и та же партия несколько раз".
- Прогнозирование принципиально отличается от классификации тем, что метки (следующий временной шаг) различаются для каждой подвыборки, которую вы кормите; классификация использует один для всей последовательности
Это резко меняет вашу функцию потерь и то, что является "хорошей практикой" для ее минимизации:
- Предиктор должен быть устойчивым к своей исходной выборке, особенно для LSTM, поэтому мы обучаемся для каждого такого "запуска", сдвигая последовательность, как вы показали.
- Поскольку метки различаются от временного шага к временному шагу, функция потерь существенно изменяется от временного шага к временному шагу, поэтому риски переобучения намного меньше.
Что я должен делать?
Во-первых, убедитесь, что вы понимаете весь этот пост, поскольку здесь нет ничего "необязательного". Тогда вот ключ к перекрытию и отсутствию перекрытия для каждой партии:
- Сдвинута одна выборка: модель учится лучше предсказывать на один шаг вперед для каждого начального шага - это означает: (1) устойчивость LSTM к начальному состоянию ячейки; (2) LSTM хорошо предсказывает любой шаг вперед с учетом X шагов позади
- Многие образцы, сдвинутые в более поздней партии: модель с меньшей вероятностью `` запомнит '' набор поездов и переобучится
Ваша цель: уравновесить два; Основное преимущество 1 над 2:
- 2 может нанести ущерб модели, заставив ее забыть увиденные образцы
- 1 позволяет модели извлекать более качественные характеристики, исследуя образец по нескольким начальным и конечным точкам (меткам) и соответствующим образом усредняя градиент.
Должен ли я когда-нибудь использовать (2) в предсказании?
- Если длина вашей последовательности очень велика и вы можете позволить себе "скользящее окно" с ~50% ее длины, возможно, но это зависит от природы данных: сигналов (ЭЭГ)? Да. Акции, погода? Сомневаюсь.
- Прогнозирование "многие-ко-многим"; чаще можно увидеть (2), в больших для более длинных последовательностей.
LSTM с отслеживанием состояния: на самом деле может быть совершенно бесполезным для вашей проблемы.
Stateful используется, когда LSTM не может обработать всю последовательность сразу, поэтому она "разбивается" - или когда требуются разные градиенты из обратного распространения. В первом случае идея такова - LSTM учитывает первую последовательность при оценке второй:
t0=seq[0:50]; t1=seq[50:100]имеет смысл;t0логически приводит кt1seq[0:50] --> seq[1:51]не имеет смысла;t1не происходит причинно изt0
Другими словами: не перекрывайте состояние в отдельных пакетах. Одна и та же партия в порядке, опять же, независимость - отсутствие "состояния" между образцами.
Когда использовать с отслеживанием состояния: когда LSTM выигрывает от рассмотрения предыдущего пакета при оценке следующего. Это может включать одношаговые прогнозы, но только если вы не можете кормить всю последовательность сразу:
- Желательно: 100 временных шагов. Может: 50. Итак, мы настроили
t0, t1как в первом пункте выше. - Проблема: не просто реализовать программно. Вам нужно будет найти способ подавать в LSTM, не применяя градиенты - например, замораживание веса или настройку
lr = 0.
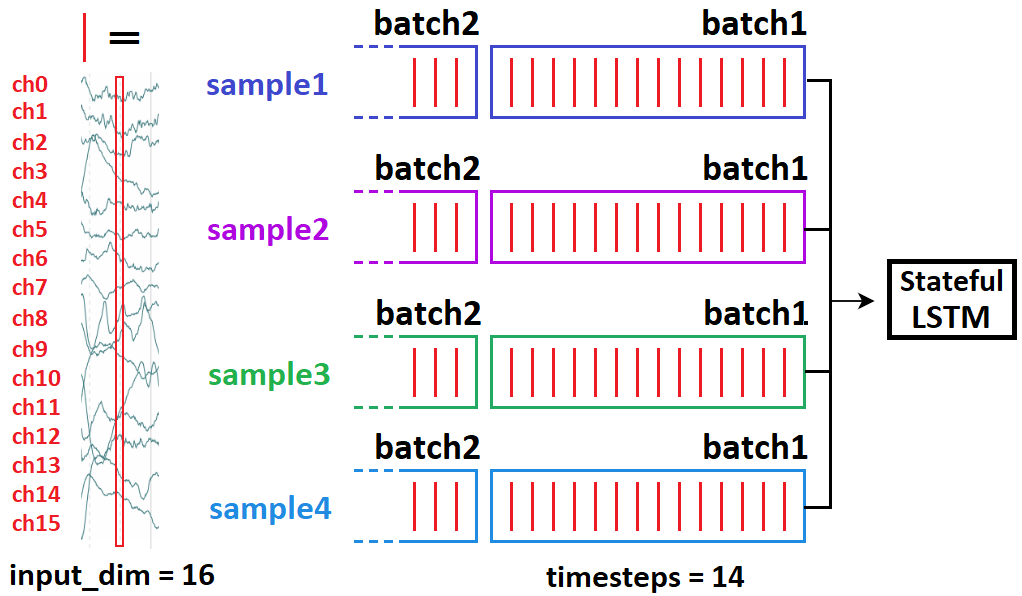
Когда и как LSTM "передает состояния" в состоянии с отслеживанием состояния?
- Когда: только от партии к партии; образцы полностью независимы
- Как: в Керасе только от партии образца к партии образца:
stateful=Trueтребует указатьbatch_shapeвместо тогоinput_shape- потому что Керас строитbatch_sizeотдельные состояния LSTM при компиляции
Как указано выше, вы не можете этого сделать:
# sampleNM = sample N at timestep(s) M
batch1 = [sample10, sample20, sample30, sample40]
batch2 = [sample21, sample41, sample11, sample31]
Из этого следует 21 причинно следует 10- и сорвут обучение. Вместо этого сделайте:
batch1 = [sample10, sample20, sample30, sample40]
batch2 = [sample11, sample21, sample31, sample41]
Партия против образца: дополнительная информация
"Пакет" - это набор образцов - 1 или больше (всегда предполагайте последнее для этого ответа). Три подхода для перебора данных: пакетный градиентный спуск (сразу весь набор данных), стохастический GD (по одной выборке за раз) и Minibatch GD (промежуточный). (Однако на практике мы также называем последний SGD и различаем только BGD - предположим, что это так для этого ответа.) Различия:
- SGD на самом деле никогда не оптимизирует функцию потерь поезда - только ее "приближения"; каждый пакет является подмножеством всего набора данных, и вычисленные градиенты имеют отношение только к минимизации потерь этого пакета. Чем больше размер партии, тем лучше ее функция потерь похожа на функцию потерь поезда.
- Вышеупомянутое может распространяться на подгонку партии к образцу: выборка является приближением партии или более плохой аппроксимацией набора данных.
- Подгонка сначала 16 образцов, а затем еще 16 - это не то же самое, что подгонка сразу 32 - поскольку веса обновляются между ними, поэтому результаты модели для второй половины будут изменяться.
- Основная причина выбора SGD вместо BGD на самом деле не в вычислительных ограничениях, а в том, что в большинстве случаев он лучше. Объясняется просто: намного проще переоснастить BGD, и SGD сходится к лучшим решениям на тестовых данных, исследуя более разнообразное пространство потерь.
БОНУСНЫЕ ДИАГРАММЫ: