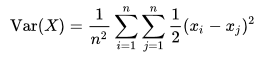Нормализовать данные, прежде чем удалять низкую дисперсию, допускает ошибки
Я тестирую iris набор данных (можно загрузить с помощью функции load_iris() от sklearn.datasets) с функциями scikit-learn normalize а также VarianceThreshold.
Кажется, что если я использую MinMaxScaler а затем запустить VarianceThreshold - функций не осталось.
Перед масштабированием:
Column: sepal length (cm) Mean: 5.843333333333334 var = 0.6811222222222223 var/mean: 0.11656398554858338
Column: sepal width (cm) Mean: 3.0573333333333337 var = 0.1887128888888889 var/mean: 0.06172466928332606
Column: petal length (cm) Mean: 3.7580000000000005 var = 3.0955026666666665 var/mean: 0.8237101295015078
Column: petal width (cm) Mean: 1.1993333333333336 var = 0.5771328888888888 var/mean: 0.48121141374837856
После масштабирования (MinMaxScaler)
Column: sepal length (cm) Mean: 0.42870370370370364 var = 0.052555727023319614 var/mean: 0.12259219262459005
Column: sepal width (cm) Mean: 0.44055555555555553 var = 0.03276265432098764 var/mean: 0.07436668067815606
Column: petal length (cm) Mean: 0.46745762711864397 var = 0.08892567269941587 var/mean: 0.19023258481745967
Column: petal width (cm) Mean: 0.4580555555555556 var = 0.10019668209876545 var/mean: 0.2187435145879658
я использую VarianceThreshold как:
from sklearn.feature_selection import VarianceThreshold
sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
Следует ли масштабировать данные (например, через MinMaxScaler) если мы хотим удалить функции с низкой дисперсией?
3 ответа
Как правило, масштабирование данных не поможет вам найти избыточные функции.
Как правило, VarianceThresholdиспользуется для удаления признаков с нулевой дисперсией, то есть констант, которые не предоставляют никакой информации. Строка в вашем кодеVarianceThreshold(threshold=(.8 * (1 - .8)))отбрасывает все функции с дисперсией ниже 0,16. И в вашем случае все функции имеют отклонение ниже этого (послеMinMaxScaler самая большая разница - ширина лепестка 0.1), так что вы выбрасываете все. Я считаю, что вы хотели оставить функции, которые вносят более 80% дисперсии, но это не то, что делает ваш код. И если вы примените эту строку раньшеMinMaxScaler, тогда все ваши функции пройдут.
Чтобы удалить функции с низкой дисперсией, вам необходимо сначала определить разумный порог для этой конкретной функции. Но в общем случае вы не можете установить жестко запрограммированный произвольный порог дисперсии, потому что для некоторых функций значение будет слишком высоким, а для других - слишком низким. Например, PCA часто используется как процедура выбора функции. Выполняется PCA и берется только K первых собственных векторов, где K выбирается таким образом, чтобы "энергия" соответствующих собственных значений составляла (скажем) 95% (или даже 80%) от суммы. Таким образом, в случаях, когда у вас есть набор данных с 50-100 функциями, вы можете уменьшить количество функций в десять раз без потери большого количества информации.
Когда вы подаете заявку StandardScalerвсе ваши функции будут центрированы и нормированы, поэтому их среднее значение будет равно нулю, а дисперсия - 1 (за исключением, конечно, констант).MinMaxScalerпо умолчанию ваши функции будут помещены в диапазон [0..1]. Вопрос не в том, какой скейлер использовать, а в том, почему вы хотите использовать скейлер. В общем случае вы не хотите выбрасывать функции без необходимости.
Предположение о том, что информация содержится в дисперсии, неверно для большинства реальных наборов данных, и во многих случаях характеристики с более низкой дисперсией не соответствуют характеристикам с низким уровнем информации. В качестве конечной цели не сокращать количество функций, а создать лучший алгоритм классификации, вам не следует слишком сильно оптимизировать промежуточные цели.
По сути, функция с низкой дисперсией означает функцию, в которой отсутствует информация. То есть, если характеристика имеет дисперсию, близкую к нулю, она может принимать постоянное значение. Однако каждая функция может представлять разное количество, поэтому ее дисперсия разная.
Например, считайте ковариатами age который может варьироваться от 0 до 100 и number_of_childsэто может быть от 0 до 5 в качестве примера. Поскольку эти две переменные принимают разные значения, они будут иметь разные дисперсии. Теперь, масштабируя функции, мы устанавливаем их в одинаковые единицы. Таким образом, мы могли сравнивать их информацию в одном масштабе.
Обратите внимание, что для набора данных диафрагмы все функции имеют одинаковый масштаб (сантиметры), то есть
from sklearn.datasets import load_iris
data = load_iris()
print(data.features_names)
>>> ['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
В этом случае хорошим первым шагом будет центрирование данных. Таким образом можно убрать с него шум.
import pandas as pd
X = pd.DataFrame(data['data'], columns=data.feature_names)
X = X - X.mean()
В MinMaxScaler использует следующую формулу:
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
Если вы проверите документацию порогового значения дисперсии и увидите формулу для дисперсии, дисперсия набора из n равновероятных значений может быть эквивалентно выражена без прямой ссылки на среднее значение в терминах квадратов отклонений всех точек друг от друга:
Итак, давайте сравним небольшой пример с двумя столбцами и тремя переменными:
a b
1 0
0 1
0 2
Без паршивости у нас есть следующие отклонения:
a: (0.5(1-0)^2+0.5(1-0)^2+ 0.5(0-1)^2 +0.5(0-0)^2 + 0.5(0-1)^2 + 0.5(0-1)^2 )/3 = (0.5+0.5+0.5+0.5)/3= 2/3 = 0.75
b: 6/3 = 2
После MinMaxScaler мы бы хотели иметь:
a b
1 0
0 0.5
0 1
и поэтому дисперсия:
a: 2/3
b: 2/3
Таким образом, с порогом 0,8 оба будут удалены после нормализации.
Итак, да, когда вы нормализуете свои данные до порога дисперсии, вы всегда будете отбрасывать больше столбцов, потому что основная идея minmaxscaler заключается в нормализации ваших данных, что означает, что у вас будет меньше дисперсии в них.