Гиперпараметрическая настройка одноклассной SVM
Я ищу пакет или "передовой" подход к автоматическому выбору гиперпараметров для одноклассной SVM с использованием ядра Gaussian(RBF). В настоящее время я реализую одноклассный svmlibsvm в R, поэтому лучше всего подойдет подход, включающий это или, по крайней мере, R.
РЕДАКТИРОВАТЬ
Чтобы дать более ясный пример того, что я ищу, допустим, у нас есть набор данных радужной оболочки глаза, и мы принимаем один из типов в качестве положительных случаев. Один из подходов состоит в том, чтобы построить одноклассную SVM с различным выбором числовых значений и гаммы, а затем проверить точность модели в отрицательных случаях (другие типы цветов). Увидеть ниже:
library(datasets)
library(data.table)
library(e1071)
#load the iris data
data(iris)
#separate positive and negative cases
positive_cases <- iris[iris$Species=="virginica",1:4]
negative_cases <- iris[iris$Species!="virginica",1:4]
#get hyperparameter choices
hyp_param_choices <- setDT(expand.grid("nu"=seq(.1,.3,by=.1),
"gamma"=1*10^seq(-2, 2, by=1)))
hyp_param_choices[,err:=0]
for(hyp_i in 1L:nrow(hyp_param_choices)){
tuned <- svm(x=positive_cases,
y=rep(T,nrow(positive_cases)), #True as they are all in the positive class
nu = hyp_param_choices[hyp_i,nu],
gamma = hyp_param_choices[hyp_i,gamma],
type='one-classification',
scale=T #scale the data
)
svm_neg_pred <- predict(tuned, #predict the negative classes, should all be false
negative_cases)
#error is sum of svm_neg_pred as this counts all the positives .i.e false positive cases divided by total number of negatives
set(hyp_param_choices, i=hyp_i, j="err", value=(sum(svm_neg_pred)/nrow(negative_cases)))
}
setorder(hyp_param_choices,err)
print(hyp_param_choices)
nu gamma err
1: 0.1 1e+00 0.00
2: 0.2 1e+00 0.00
3: 0.3 1e+00 0.00
4: 0.1 1e+01 0.00
5: 0.2 1e+01 0.00
6: 0.3 1e+01 0.00
7: 0.1 1e+02 0.00
8: 0.2 1e+02 0.00
9: 0.3 1e+02 0.00
10: 0.3 1e-02 0.01
11: 0.2 1e-01 0.01
12: 0.2 1e-02 0.02
13: 0.3 1e-01 0.02
14: 0.1 1e-01 0.03
15: 0.1 1e-02 0.05
По правде говоря, у моей проблемы есть несколько ложных срабатываний в данных обучения. Мы могли бы включить это в пример, добавив образец негативов к позитивным и исключив эти негативы из проверочного тестирования, а затем повторно запустив:
positive_cases <- rbind(iris[iris$Species=="virginica",1:4],
iris[iris$Species!="virginica",1:4][sample(nrow(iris[iris$Species!="virginica",]),
10),])
Я ищу другой подход к выбору лучших гиперпараметров одного класса в статье или иным образом, у которого есть некоторые основания для того, чтобы быть хорошим подходом.
Чтобы дать некоторую предысторию, мне известно об исходной реализации одноклассных SVM, разработанной Шолкопфом и др. и понять, что цель подхода состоит в том, чтобы сопоставить данные одного класса с пространством функций, соответствующим ядру, и отделить их от источника с максимальным запасом с помощью гиперплоскости. В этом смысле происхождение можно рассматривать как все другие классы. Мне также известно о SVDD, введенных Tax & Duin. Цель здесь - создать как можно меньшую сферу, охватывающую данные. Благодаря этому подходу все точки вне сферы являются другими классами / выбросами. Я также знаю, что эти два подхода приводят к эквивалентным функциям минимизации при использовании гауссова ядра. Оба этих подхода используют мягкие поля, позволяющие ошибочно классифицировать случаи и в одном классе. Поскольку они эквивалентны, я буду говорить только о OC-SVM, но подходы с использованием SVDD в качестве ответа также были бы очень признательны!
Итак, в моей проблеме мой одноклассный - это положительные случаи, для которых я хочу оптимизировать nu, относящуюся к пропорции неправильно классифицированных случаев (ложные срабатывания) и гаммы, ширины гауссовского ядра. В моей проблеме я знаю, что будут ложные срабатывания, это природа проблемы, и ее невозможно обнаружить. Я также хочу применить несколько OC-SVM к разным наборам данных, поэтому мне нужен автоматизированный подход к настройке ню и гаммы на основе доли выбросов, присутствующих в рассматриваемом наборе данных, и скрытых функций данных.
Поскольку эта проблема практически не контролируется, я, очевидно, не могу использовать CV обычным образом с диапазоном nu и gamma, поскольку тогда будет выбрано решение с минимальным расстоянием от начала координат. Просто отметим, что у меня есть отрицательные случаи, но я бы предпочел удерживать их, если это возможно, на этапе проверки, как будто нет, зачем вообще беспокоиться о одноклассовом подходе и почему бы не использовать нормальный двухклассовый подход?
Мой вопрос в том, нашел ли кто-нибудь пакет или подход для этого в R? Я знаю, что в научной литературе есть множество подходов, в том числе очень многообещающие: DTL и здесь, но у них, похоже, нет кода, запрещающего псевдокод, и, например, как перевести это на R и включить его с libsvm, кажется большим шаг за мои текущие способности.
Любая помощь или предложения будут приняты с благодарностью!
1 ответ
Ваш вопрос о svmреализация. Здесь я включаю эскиз дляsvm ниже RBFконтекст. Реализация в этом посте используетcaret и метод взят из kernlabпакет. Далее пример с использованиемiris набор данных с Speciesполиномиальный. Я набросал тренировочную сторону, но тестовую часть легко сделать, используяpredict() по набору тестов и матрицам путаницы из тех же caret или мультиклассовый аврок.
Метод также учитывает перекрестную проверку с cv=10:
#Some libraries
library(rsample)
library(caret)
library(visdat)
library(recipes)
#Data
data(iris)
# Create training (70%) and test (30%) sets
set.seed(123)
split_strat <- initial_split(iris, prop = 0.7,
strata = 'Species')
train_strat <- training(split_strat)
test_strat <- testing(split_strat)
#Tuning a SVM model
# Tune an SVM with radial basis kernel
set.seed(1854) # for reproducibility
model_svm <- caret::train(
Species ~ .,
data = train_strat,
method = "svmRadial",
trControl = trainControl(method = "cv", number = 10),
tuneLength = 10
)
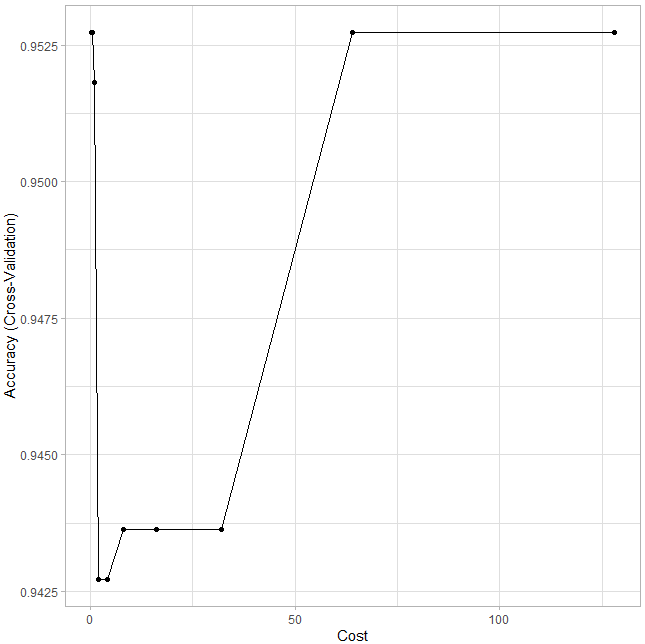
# Plot results
ggplot(model_svm) + theme_light()
Вы можете пойти глубже и изучить метод, который ищет kernlab который включает в себя дополнительные параметры настройки, которые могут быть добавлены в caretфреймворк. Надеюсь, это может быть вам полезно.