Как 3d реконструировать надежно из нескольких изображений с известными позами в OpenCV

Question

Традиционное решение для примеров изображений с высоким разрешением:

1. Извлечь особенности (плотные) для всех изображений
2. сопоставлять функции, чтобы найти треки по изображениям
3. триангулировать элементы до 3d точек.

Здесь я могу дать две проблемы для моего случая (много изображений 640*480 с небольшим перемещением между ними), во- первых: сопоставление очень медленное, особенно если количество изображений большое, поэтому лучшим решением может быть отслеживание оптического потока., но это становится редким с большими движениями, (соединение могло решить проблему!!)

во-вторых: триангуляционные треки, хотя это слишком определенная проблема, мне трудно кодировать решение, (здесь я прошу упростить то, что я читаю в ссылках)

Я довольно долго искал библиотеки в этом направлении, но безрезультатно.

Опять же, у меня есть базовые матрицы истинных камер, и мне нужна только 3D-позиция в качестве первой оценки (без БА). Кодовое программное решение может оказать большую помощь, так как мне не нужно изобретать велосипед, хотя подробные инструкции могут быть полезны

Answer 1

это в основном показывает базовую геометрию для оценки глубины.

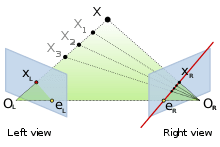
Как вы сказали, у нас есть поза камеры Q, и мы выбираем точку X из мира, X_L - это проекция на левое изображение, теперь с помощью Q_L, Q_R и X_L мы можем создать эту эпиполярную плоскость зеленого цвета, остальная работа проста, мы ищем точки на линии (Q_L, X), эта строка точно описывает глубину X_L, с разными предположениями: X1, X2,..., мы можем получить разные проекции на правом изображении

Теперь мы сравним разницу в интенсивности пикселей от X_L и репроецированной точки на правом изображении, просто выберите наименьшую из них, и соответствующая глубина будет именно такой, какой мы хотим.

Довольно просто, эй? На самом деле все намного сложнее, изображение никогда не бывает строго выпуклым:

Это делает наше сопоставление чрезвычайно сложным, поскольку невыпуклая функция приведет к тому, что любая функция расстояния будет иметь несколько критических точек (подходящих совпадений), как вы решите, какая из них правильная?

Тем не менее, люди предложили сопоставление на основе пути для решения этой проблемы, такие методы, как: SAD, SSD, NCC, они вводятся для создания функции расстояния как можно более выпуклой, тем не менее, они не могут справиться с проблемой повторяющейся крупномасштабной текстуры и проблемой низкой текстуры.

Чтобы решить эту проблему, люди начинают искать в эпиполярной линии на большом расстоянии и внезапно обнаруживают, что мы можем описать все это распределение совпадающих показателей на расстоянии по глубине.

Горизонтальная ось - глубина, а вертикальная ось - соответствие метрической оценки, и на этой иллюстрации мы нашли фильтр глубины, и мы обычно описываем это распределение с помощью гауссовского, также известного как гауссовского фильтра глубины, и используем этот фильтр для описания неопределенности глубины. в сочетании с методом сопоставления патчей мы можем примерно получить предложение.

А теперь давайте воспользуемся некоторыми инструментами оптимизации, такими как GN или градиентный спуск, чтобы окончательно уточнить оценку глубины.

Подводя итог, общий процесс оценки глубины похож на следующие этапы:

1. принять всю глубину во всех пикселях в соответствии с начальным гауссовым распределением
2. начать поиск по эпиполярной линии и перепроецировать точки в целевой кадр
3. триангулировать глубину и рассчитать неопределенность глубины по глубинному фильтру
4. запустите 2 и 3 еще раз, чтобы получить новое распределение глубины и объединить с предыдущим, если они сходятся, то прервите, иначе начните снова с 2.