Нахождение наибольшего подмножества точек, образующих выпуклый многоугольник
Я ищу алгоритм для нахождения наибольшего подмножества точек (по наибольшему я имею в виду число), которые образуют выпуклый многоугольник из данного набора точек. Я думаю, что это может быть решено с помощью DP, но я не уверен. Возможно ли сделать это в O(n^3)? На самом деле мне просто нужен размер наибольшего подмножества, поэтому для него не нужно иметь уникальное решение
Редактировать:
просто чтобы сохранить это простым,
Заданный вход: набор точек в 2D
Желаемый результат: максимальное количество точек, которые образуют выпуклый многоугольник, как в примере, выходное значение равно 5 (ABHCD является одним из возможных выпуклых многоугольников)
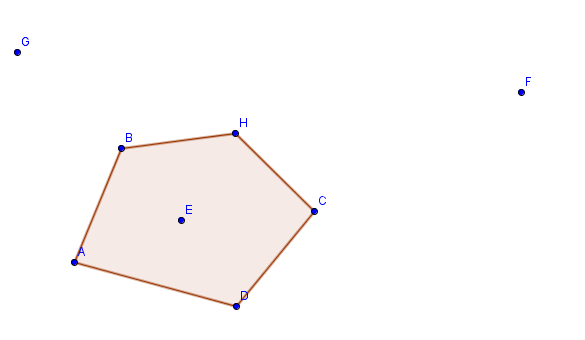
Есть похожая проблема spoj.com/problems/MPOLY, которая решается с помощью DP в O(N^3), мой вопрос об обобщении этой проблемы, которая не должна содержать (0,0)
4 ответа
Эта проблема уже была опубликована в этих соревнованиях:
- SPOJ проблема BOYSCOUT
- Задача USACO DEC08 "Самый большой забор" (последняя проблема на странице)
И его решение (алгоритм O (N3)) можно найти на этой странице: "Анализ" ограждения "задачи USACO DEC08" Брюса Мерри и Джейкоба Стейнхардта.
Ниже приведена попытка объяснить этот алгоритм. Также здесь моя реализация этого алгоритма в C++11. Этот код работает для N<=250 и целочисленных координат в диапазоне 0 .. 1023. На одной линии не должно быть трех точек. Вот скрипт Python, который генерирует тестовые данные, удовлетворяющие этим требованиям.
O (N2) алгоритм для упрощенной задачи
Упрощенная задача: найти наибольшее подмножество точек, которые образуют выпуклый многоугольник и содержат крайнюю левую точку данного набора (или, если имеется несколько крайних левых точек, этот многоугольник должен содержать самые верхние из них).
Чтобы решить эту проблему, мы могли бы соединить каждую пару точек направленным отрезком, а затем (неявно) обработать каждый отрезок как узел графа, как показано на диаграмме:
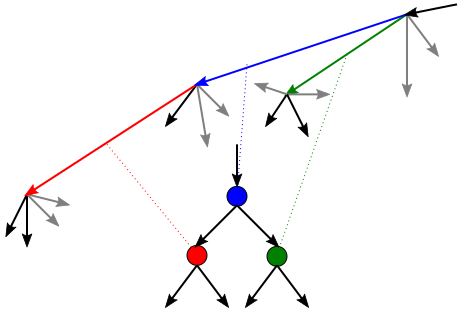
Здесь родительский узел и соответствующий сегмент имеют синий цвет. Сегмент линии, соответствующий его левому дочернему элементу (красного цвета), начинается в конце "родительского" сегмента, и это тот отрезок, который делает наименьший возможный поворот влево относительно направления "родительского" сегмента. Сегмент линии, соответствующий его правому дочернему элементу (зеленый цвет), начинается в начале "родительского" сегмента, и это также сегмент линии, делающий наименьший возможный поворот влево относительно направления "родительского" сегмента.
Любой сегмент, заканчивающийся в крайней левой точке, соответствует "листовому" узлу, то есть не имеет дочерних узлов. Такое построение графа гарантирует отсутствие циклов, иными словами, этот граф является DAG.
Теперь, чтобы найти наибольшее выпуклое подмножество точек, достаточно найти самый длинный путь в этом графе. А самый длинный путь в DAG можно найти с помощью алгоритма динамического программирования за время O(E), где E - количество ребер в графе. Поскольку каждый узел имеет только 2 исходящих ребра, каждое из которых соответствует паре точек, эта проблема может быть решена за O (N2) времени.
Все это можно реализовать, если предварительно обработать входные данные, отсортировав направленные отрезки, начиная с одной точки по углу. Это позволяет выполнить первоочередной проход по графику. Мы должны запомнить самый длинный путь, начиная с каждого обработанного узла, чтобы каждый край графа посещался не более одного раза, и у нас есть алгоритм времени O (E) = O (N2) (пока игнорируем время предварительной обработки). Требования к пространству также O (N2), потому что нам нужно хранить отсортированные направления для каждой пары точек, а запоминание использует одно значение на узел (которое также является парой точек).
Вот реализация C++ этого алгоритма динамического программирования:
unsigned dpStep(ind_t i_left, ind_t from, ind_t to_ind)
{
ind_t child = sorted[from][to_ind];
while (child < i_left)
child = sorted[from][++to_ind];
if (child == i_left)
return 1;
if (auto v = memorize[from][child])
return v;
const auto x = max(dpStep(i_left, child, lefts[from][child]) + 1,
dpStep(i_left, from, static_cast<ind_t>(to_ind + 1)));
memorize[from][child] = static_cast<ind_t>(x);
return x;
}
Входными параметрами являются крайняя левая точка и пара точек, образующих текущий сегмент линии (где начальная точка сегмента задается непосредственно, а конечная точка задается в качестве индекса в отсортированном по углу массиве точек). Слово "левый" в этом фрагменте кода слегка злоупотреблено: оно означает как крайнюю левую точку (i_left) и предварительно обработанный массив, содержащий левые дочерние элементы для графа (lefts[][]).
O (N3) алгоритм
Общая проблема (где крайняя левая точка не зафиксирована) может быть решена следующим образом:
- Сортировка точек влево-вправо
- Предварительно обработайте точки, чтобы получить два массива: (a) каждая точка, отсортированная по направлению относительно друг друга, и (b) позиция в первом массиве конца отрезка, делающая наименьший возможный поворот налево относительно направления "родительского" отрезка.
- Используйте каждую точку как крайнюю левую точку и найдите самый длинный выпуклый многоугольник с "упрощенным" алгоритмом.
- Периодически удаляйте все точки слева от "самой левой" точки из предварительно обработанных массивов.
- Возьмите самый длинный путь, найденный на шаге 3.
Шаг 4 не является обязательным. Это не улучшает O (N3) временную сложность. Но это немного улучшает скорость алгоритма DP, исключая ненужные точки. В моих тестах это дает увеличение скорости на 33%.
Есть несколько альтернатив для предварительной обработки. Мы могли бы вычислить каждый угол (с atan2) и отсортировать их, как это сделано в примере кода Брюсом Мерри и Джейкобом Стейнхардтом. Это самый простой способ, но atan2 может быть слишком дорогим, особенно для небольших наборов точек.
Или мы могли бы исключить atan2 и сортировать касательные вместо углов, как это сделано в моей реализации. Это немного сложнее, но быстрее.
Обе эти альтернативы требуют времени O (N2 log N) (если мы не используем некоторую сортировку распределения). Третий вариант - использовать хорошо известные методы вычислительной геометрии (аранжировки и двойственность), чтобы получить предварительную обработку O (N2). Но я не думаю, что это полезно для нашей проблемы: он, вероятно, слишком медленный для меньших наборов точек из-за большого постоянного коэффициента, а для больших наборов точек это может дать некоторое улучшение скорости, но слишком незначительное, потому что шаг 3 будет значительно перевешивать Шаг 2. Также это гораздо сложнее реализовать.
Некоторые другие результаты: я попытался реализовать итеративный DP вместо рекурсии; это не заметно изменило скорость. Также я попытался выполнить два поиска DP одновременно, чередуя шаги каждого поиска (что-то похожее на волокна или HyperThreading, реализованные в программном обеспечении); это может помочь, потому что DP состоит в основном из обращений к памяти с высокой задержкой и предотвращением полного использования пропускной способности процессора; результаты не очень впечатляющие, только увеличение скорости примерно на 11%, скорее всего, с реальным HyperThreading это будет намного быстрее.
Я думаю, что придумал алгоритм для этого, расширив алгоритм Эндрю для выпуклых оболочек.
Первоначально я придумал алгоритм O(N^4), но заметил, что он сильно усложнил его и привел к алгоритму O(N^2). Кажется, что где-то может быть ошибка в коде, которая вызывает проблемы, по крайней мере, в случае вертикальной линии точек. Это может быть особый случай (требующий изменения нескольких строк кода) или признак большего недостатка в алгоритме. Если это последнее, то я склонен сказать, что это NP-сложный, и предложить алгоритм как эвристический. Я потратил все время на программирование и отладку. В любом случае, кажется, что работает нормально в других случаях. Тем не менее, трудно проверить правильность, когда правильные алгоритмы кажутся O(2^N).
def maximal_convex_hull(points):
# Expects a list of 2D points in the format (x,y)
points = sorted(set(points)) # Remove duplicates and sort
if len(points) <= 1: # End early
return points
def cross(o, a, b): # Cross product
return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])
# Use a queue to extend Andrew's algorithm in the following ways:
# 1. Start a new convex hull for each successive point
# 2. Keep track of the largest convex hull along the way
Q = []
size = 0
maximal_hull = None
for i,p in enumerate(points):
remaining = len(points) - i + 1
new_Q = []
for lower, upper in Q: # Go through the queue
# Build upper and lower hull similtanously, slightly less efficent
while len(lower) >= 2 and cross(lower[-2], lower[-1], p) < 0:
lower.pop()
lower.append(p)
while len(upper) >= 2 and cross(upper[-2], upper[-1], p) > 0:
upper.pop()
upper.append(p)
new_size = len(lower) + len(upper)
if new_size > size: # Check for a new highest maximal convex hull
size = new_size
maximal_hull = (lower, upper)
# There is an odd bug? that when one or both if statements are removed
# xqg237.tsp (TSPLIB) gives slightly different solutions and is
# missing a number of points it should have.
# Seems like if the opposite should be true if anything since they
# were intended to be easy optimizations not required code.
if remaining + new_size >= size: # Don't bother if not enough
new_Q.append((lower, upper)) # Add an updated convex hulls
if remaining > size: # Don't bother if not enough
new_Q.append(([p], [p])) # Add a new convex hull
Q = new_Q # Update to the new queue
# Extract and merge the lower and upper to a maximium convex hull
# Only one of the last points is ommited because it is repeated
# Asserts and related variables used for testing
# Could just have "return lower[:-1] + list(reversed(upper[:-1]))[:-1]"
lower, upper = maximal_hull
max_hull_set = set(lower) | set(lower) | set(upper)
lower = lower
upper = list(reversed(upper[:-1]))[:-1]
max_convex_hull = lower + upper
assert len(lower) + len(upper) == len(max_hull_set)
assert max_hull_set == set(max_convex_hull)
return max_convex_hull
Изменить: Этот алгоритм не является правильным, но он послужил вдохновением для правильного алгоритма, и поэтому я оставляю его здесь.
Это мой алгоритм динамического программирования O(N^4) с идеей из алгоритма Эндрю, опубликованного Nuclearman, я все еще ищу алгоритм O(N^3)
upper_hull(most left point, previous point, current point)
{
ret = 0
if (current point != most left point) /* at anytime we can decide to end the upper hull and build lower_hull from current point ending at most left point */
ret = min(ret,lower_hull(most left point, -1, current point))
for all point on the right of current point /* here we try all possible next point that still satisfy the condition of convex polygon */
if (cross(previous point,current point,next point) >= 0) max(ret,1+upper_hull(most left point, current point, next point))
return ret;
}
lower_hull(most left point, previous point, current point)
{
if (current point == most left point) return 0;
ret = -INF /* it might be impossible to build a convex hull here, so if it does it will return -infinity */
for all point on the left of current point and not on the left of most left point
if (cross(previous point,current point,next point) >= 0) max(ret,1+lower_hull(most left point, current point, next point))
return ret;
}
Сначала отсортируйте точку на основе оси x, затем для сортировки связывания по оси y, затем попробуйте всю точку как самую левую точку для запуска upper_hull(p,-1,p), скажите, пожалуйста, есть ли в этом алгоритме изъян
Вы можете использовать триангуляцию Делоне и удалить самый длинный край, а также вершину. Я использую аналогичный алгоритм, чтобы найти вогнутый корпус. Вы можете найти пример на основе данных о населении @ http://www.phpdevpad.de/geofence. Я также написал php класс concave-hull @ phpclasses.org.