Как выполнить нелинейную подгонку данных к данным эксперимента

У меня есть некоторые экспериментальные данные. Таким образом, мне нужно установить следующую функцию, чтобы определить одну из переменных. В этой процедуре использовался алгоритм наименьших квадратов Левенберга – Марквардта.

Я использовал вариант подгонки кривой в программном обеспечении Igor Pro. Я определил новую функцию подгонки и попытался определить независимую и зависимую переменную. Тем не менее, я не знаю, по какой причине я получил эту ошибку:

"Функция подбора вернула INF как минимум для одной переменной X"

Моя функция:

sin(theta) = -1+2*sqrt(alpha/x)*exp(-beta*(x-alpha)^2)

beta = 1.135e-4;

sin(theta) = [-0.81704 -0.67649 -0.83137 -0.73468 -0.66744 -0.43602 0.45368 0.75802 0.96705 0.99717 ]

x = [72.01 59.99 51.13 45.53 36.15 31.66 30.16 29.01 25.62 23.47 ]

Есть ли предложение найти alpha переменная здесь?

Есть ли какое-нибудь удобное программное обеспечение или программа для нелинейного подбора кривой?

Источник

3 ответа

В gnuplot это будет выглядеть так. Подгонка не очень хорошая, но это не "ошибка" gnuplot, но, очевидно, эти данные не могут быть очень хорошо приспособлены к этой функции.

Код:

### nonlinear curve fitting
reset session

$Data <<EOD
72.01 -0.81704
59.99 -0.67649
51.13 -0.83137
45.53 -0.73468
36.15 -0.66744
31.66 -0.43602
30.16 0.45368
29.01 0.75802
25.62 0.96705
23.47 0.99717
EOD

f(x) = -1+2*sqrt(alpha/x)*exp(-beta*(x-alpha)**2)

# initial guessed values
alpha = 25
beta = 1
set fit nolog results
fit f(x) $Data u 1:2 via alpha,beta

plot $Data u 1:2 w lp pt 7, \
    f(x) lc rgb "red"

print sprintf("alpha=%g, beta=%g",alpha,beta)
### end of code

Результат:

alpha=25.818, beta=0.0195229

ht tps://i.sta ck.imgur.com/3lb60.png

Источник

Matlab

Я немного изменил функцию, -1 изменился на -gamma и оптимизировать, чтобы найти gamma

Код следующий

ydata =  [-0.81704 -0.67649 -0.83137 -0.73468 -0.66744 -0.43602 0.45368...
    0.75802 0.96705 0.99717 ];
xdata = [72.01 59.99 51.13 45.53 36.15 31.66 30.16 29.01 25.62 23.47 ];

sin_theta = @(alpha, beta, gamma, xdata) -gamma+2.*sqrt(alpha./xdata).*exp(beta.*(xdata-alpha).^2);

%Fitting function as function of array(x) required by lsqcurvefit
f = @(x,xdata) sin_theta(x(1),x(2), x(3),xdata);
% [alpha, beta, gamma]
x0 = [25, 0, 1] ;

options = optimoptions('lsqcurvefit','Algorithm','levenberg-marquardt', 'FunctionTolerance', 1e-30);


[x,resnorm,residual,exitflag,output] = lsqcurvefit(f,x0,xdata,ydata,[], [], options);

% Accuracy 
RMSE = sqrt(sum(residual.^2)/length(residual));

alpha = x(1); beta = x(2); gamma = x(3);

%Plotting data
data = linspace(xdata(1),xdata(end));
plot(xdata,ydata,'ro',data,f(x,data),'b-', 'linewidth', 3)
legend('Data','Fitted exponential')
title('Data and Fitted Curve')
set(gca,'FontSize',20)

Результат

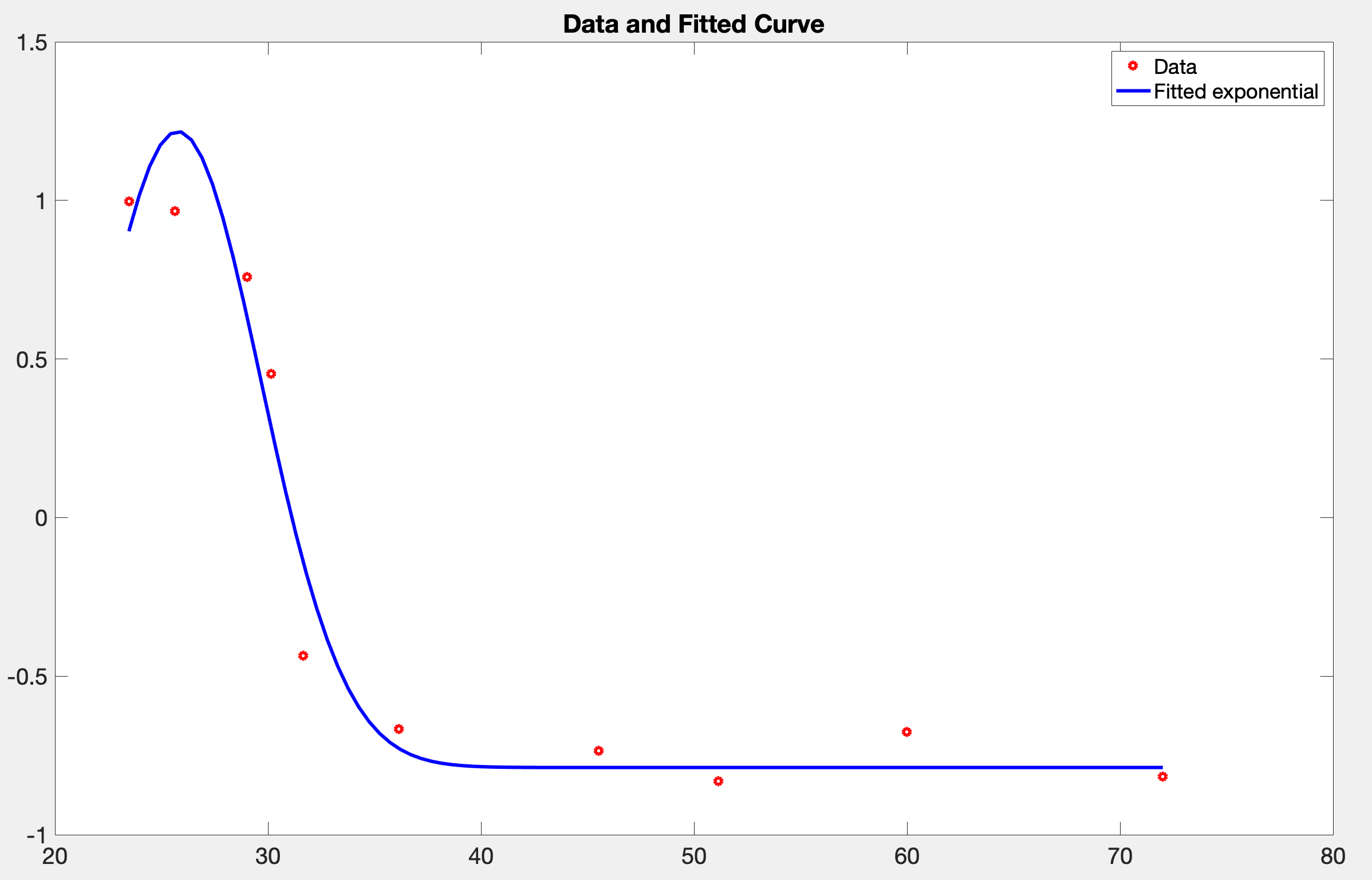
alpha = 26.0582, beta = -0.0329, gamma = 0.7881 instead of 1, RMSE = 0.1498

график

Источник

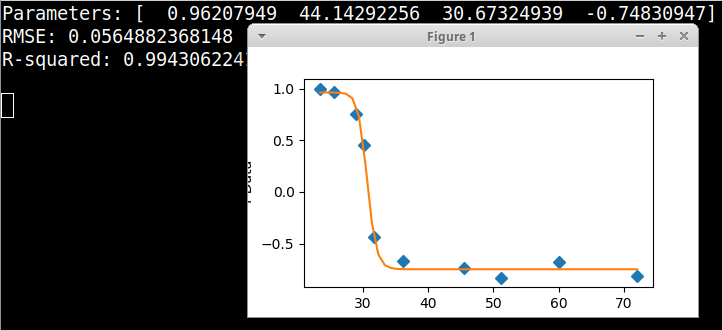
Если это может быть чем-то полезным, то поиск по моим уравнениям по вашим данным оказался в хорошем соответствии со стандартным 4-параметрическим логистическим уравнением "y = d + (a - d) / (1.0 + pow(x / c, b))"с параметрами a = 0,96207949, b = 44,14292256, с = 30,67324939 и d = -0,74830947, что дает RMSE = 0,0565 и R-квадрат = 0,9943, и я включил код для графического установщика Python, используя это уравнение.

import numpy, scipy, matplotlib
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit


theta = [-0.81704, -0.67649, -0.83137, -0.73468, -0.66744, -0.43602, 0.45368, 0.75802, 0.96705, 0.99717]
x = [72.01, 59.99, 51.13, 45.53, 36.15, 31.66, 30.16, 29.01, 25.62, 23.47]

# rename to match previous example code
xData = numpy.array(x)
yData = numpy.array(theta)

# StandardLogistic4Parameter equation from zunzun.com
def func(x, a, b, c, d):
    return  d + (a - d) / (1.0 + numpy.power(x / c, b))


# these are the same as the scipy defaults
initialParameters = numpy.array([1.0, 1.0, 1.0, 1.0])

# curve fit the test data
fittedParameters, pcov = curve_fit(func, xData, yData, initialParameters)

modelPredictions = func(xData, *fittedParameters) 

absError = modelPredictions - yData

SE = numpy.square(absError) # squared errors
MSE = numpy.mean(SE) # mean squared errors
RMSE = numpy.sqrt(MSE) # Root Mean Squared Error, RMSE
Rsquared = 1.0 - (numpy.var(absError) / numpy.var(yData))

print('Parameters:', fittedParameters)
print('RMSE:', RMSE)
print('R-squared:', Rsquared)

print()


##########################################################
# graphics output section
def ModelAndScatterPlot(graphWidth, graphHeight):
    f = plt.figure(figsize=(graphWidth/100.0, graphHeight/100.0), dpi=100)
    axes = f.add_subplot(111)

    # first the raw data as a scatter plot
    axes.plot(xData, yData,  'D')

    # create data for the fitted equation plot
    xModel = numpy.linspace(min(xData), max(xData))
    yModel = func(xModel, *fittedParameters)

    # now the model as a line plot
    axes.plot(xModel, yModel)

    axes.set_xlabel('X Data') # X axis data label
    axes.set_ylabel('Y Data') # Y axis data label

    plt.show()
    plt.close('all') # clean up after using pyplot

graphWidth = 800
graphHeight = 600
ModelAndScatterPlot(graphWidth, graphHeight)
Источник
Другие вопросы по тегам