Принятие-отклонение для бета-версии кода R

Question

Я использую метод принятия-отклонения для бета-распределения с g(x) = 1, 0 ≤ x ≤ 1. Функция: f(x) = 100x^3(1-x)^2.

Я хочу создать алгоритм для генерации данных из этой функции плотности.

Как я могу оценить P(0 ≤ X ≤ 0,8) при k = 1000 повторений (n=1000)? Как я могу решить это в R?

У меня уже есть:

beta.rejection <- function(f, c, g, n) {
naccepts <- 0
result.sample <- rep(NA, n)

  while (naccepts < n) {
    y <- runif(1, 0, 0.8)
    u <- runif(1, 0, 0.8)

    if ( u <= f(y) / (c*g(y)) ) {
      naccepts <- naccepts + 1
      result.sample[n.accepts] = y
    }
  }

  result.sample
}

f <- function(x) 100*(x^3)*(1-x)^2
g <- function(x) x/x
c <- 2

result <- beta.rejection(f, c, g, 10000)

for (i in 1:1000){ # k = 1000 reps
  result[i] <- result[i] / n
}

print(mean(result))

Answer 1

Вы близки, но есть несколько проблем:

1) опечатка с naccepts против n.accepts

2) Если вы не собираетесь использовать g тогда вы не должны жестко runif() как функция, которая генерирует случайные величины, которые распределяются в соответствии с g, Функция rejection (почему жесткий провод в beta?) Также должна быть передана функция, которая способна генерировать соответствующие случайные величины.

3) u должен быть взят из [0,1] не [0,0.8], 0.8 не должны участвовать в генерации ценностей, только их интерпретация.

4) c должна быть верхняя граница для f(y)/g(y), 2 слишком мало Почему бы не взять производную f найти его макс? 3,5 работает. Также -- c не хорошее имя для переменной в R (из-за функции c()). Почему бы не назвать это M?

Внесение этих изменений приводит к:

rejection <- function(f, M, g, rg,n) {
  naccepts <- 0
  result.sample <- rep(NA, n)

  while (naccepts < n) {
    y <- rg(1)
    u <- runif(1)

    if ( u <= f(y) / (M*g(y)) ) {
      naccepts <- naccepts + 1
      result.sample[naccepts] = y
    }
  }

  result.sample
}

f <- function(x) 100*(x^3)*(1-x)^2
g <- function(x) 1
rg <- runif
M <- 3.5 #upper bound on f (via basic calculus)

result <- rejection(f, M, g,rg, 10000)

print(length(result[result <= 0.8])/10000)

Типичный вывод: 0.9016

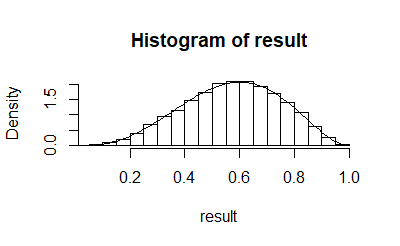
Вы также можете сделать гистограмму плотности result и сравните его с теоретическим бета-распределением:

> hist(result,freq = FALSE)
> points(seq(0,1,0.01),dbeta(seq(0,1,0.01),4,3),type = "l")

Совпадение довольно хорошее: