Что означает оценка базовой функции сплайна?

Question

Я пытаюсь понять рабочий процесс для реализации базовой функции bspline.

tauf    Vd
0        0
0.048   502.8944826
0.072   743.5034753
0.096   791.2514106
0.12    825.3244319
0.144   858.1731717
0.168   889.1381766
0.192   922.4214306
0.216   952.9989296
0.24    982.8650001

Результат basisValueMat_f:

1.000   0.000   0.000   0.000   0.000   0.000
0.000   0.076   0.551   0.364   0.009   0.000
0.000   0.013   0.393   0.533   0.062   0.000
0.000   0.000   0.234   0.596   0.170   0.000
0.000   0.000   0.121   0.547   0.331   0.001
0.000   0.000   0.057   0.420   0.496   0.027
0.000   0.000   0.023   0.273   0.591   0.114
0.000   0.000   0.007   0.140   0.570   0.283
0.000   0.000   0.001   0.044   0.408   0.547
0.000   0.000   0.000   0.001   0.085   0.914
0.000   0.000   0.000   0.000   0.000   1.000

Графическое представление:

https://i.imgur.com/41q0lDH.jpg

Код:

norder = 4;    % degree - 1
nbreaks = 2;
nbasis = nbreaks + norder - 2;
breaks = linspace(0,taufmax,nbreaks)';
wtaubasis = create_bspline_basis([0,max(breaks)], nbasis, norder, breaks);
basisValueMat_f = full(eval_basis(wtaubasis, tauf)); 

Пожалуйста, помогите мне понять, что делать create_bspline_basis и eval_basis функции делают. Мне нужно иметь математическую интерпретацию этой информации.

Answer 1

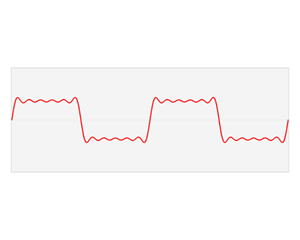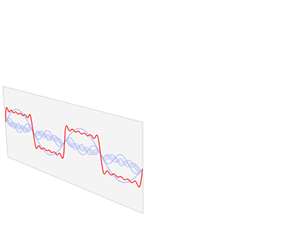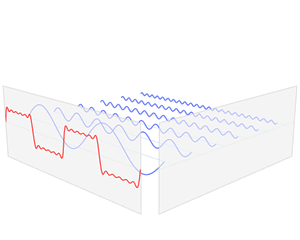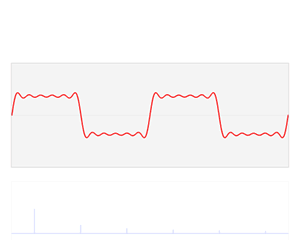
Базисные функции подобны "строительным блокам" для аппроксимации функций в интервале. Как видно из графика, несколько базовых функций используются для аппроксимации функции источника. Чем сложнее исходная функция, тем больше базисных функций потребуется для ее аппроксимации с определенной ошибкой. Посмотрите на эту анимацию, объясняющую ряд Фурье прямоугольной волны:

Преобразование Фурье (FT; показано на анимации выше как синий S(f)) показывает ту же информацию, что и "срез" вашей диаграммы:

Разница в том, что в примере FT из Википедии величины базисных функций (которые являются синусами и / или косинусами) постоянны на протяжении всего интервала, но в вашем примере со сплайн-интерполяцией величины базисных функций (которые являются полиномами) изменяются плавно на протяжении всего интервала.

Наконец, чтобы ответить на ваш вопрос, оценка базисных функций может сказать вам, какая из базисных функций является наиболее доминирующей в данной точке (или интервале). Одно из применений, которое я могу придумать для этого, - если какая-то функция гораздо более доминирующая, чем другие (как в случае с точкой "1" на вашей диаграмме), "несущественными" функциями можно полностью пренебречь, сохраняя при этом справедливую общую интерполяцию. точный - что может иметь некоторые вычислительные преимущества.