Что такое хороший алгоритм для генерации случайного пути?

Question

Мне нужно сгенерировать случайный путь с 25 сегментами, который никогда не пересекает себя между двумя точками в области 1000x1000. Какой хороший алгоритм для этого?

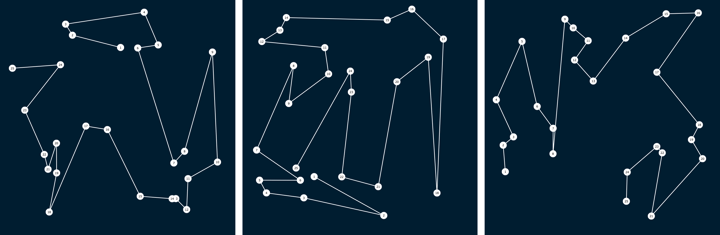
Моя первоначальная идея, которая дает хорошие результаты, заключалась в том, чтобы сгенерировать случайный многоугольник, используя метод разделения пространства, а затем удалить одну сторону.

Результаты выглядят так:

Недостатком этого метода является то, что начало всегда довольно близко к концу (так как они изначально были связаны линией).

Другим недостатком является то, что, поскольку они были многоугольником, общая форма создает некоторую форму или искаженный круг. Существует множество типов путей, которые никогда не будут сгенерированы, например спираль.

Кто-нибудь знает алгоритм, который мог бы помочь мне генерировать эти пути?

Answer 1

Вот идея (отказ от ответственности: вне моей головы, не проверено, не подтверждено или что-нибудь...):

Нарисуйте случайные координаты и "попытайтесь" соединить линии в том порядке, в котором вы их рисуете - поэтому у вас есть P1_{(x1, y1),} затем P2_{(x2, y2),} и вы соединяете их, затем P3_{(x3, y3)} и до тех пор, пока пересечение отсутствует создается (вы должны проверять это каждый раз), вы продолжаете рисовать и подключаться. В конце концов, будет сгенерировано пересечение - затем вы попытаетесь соединить последнюю точку (Pn-1: перед вновь созданной точкой) с более ранней из двух точек, образующих пересекающуюся линию (назовем их Pi & Pi + j. Если это действительно (то есть, это не пересекает никакую другую линию), вы отключаете эту линию (Pi + j больше не идет после Pi), вы соединяете Pi с Pn-1 и возобновляете работу с Pi + j (который теперь становится Pn-1 в условия порядка точек). Если подключение Pn-1 к Pi недопустимо, вы делаете то же самое, но с недавно найденным пересечением.

В конце концов вы разрешите пересечение (я) и подключитесь к самой последней точке - Pn, и вы сможете возобновить ее как обычно.

Очевидным недостатком этого алгоритма является то, что он имеет очень опасную сложность времени Big-O, но он должен быть способен генерировать все виды путей.

С точки зрения структуры данных реализации двусвязный список выглядит как непосредственный кандидат.

Answer 2

Триангуляция набора точек с последующим переходом по краям - это решение, позволяющее избежать проблемы с «круговыми» путями, которые имеют обходные пути на основе многоугольников.

Вероятно, вам не нужен случайный набор точек, который имеет точки слишком близко друг к другу, потому что это может привести к тому, что путь будет выглядеть так, как будто он пересекает себя в определенных точках. По этой причине рекомендуется использовать что-то вроде метода выборки диска Пуассона для генерации набора точек - триангуляция такого набора точек обеспечит случайный путь с сегментами более или менее равной длины, с углами сегмента-сегмента примерно 60° и без видимых точек пересечения.

Алгоритм

Имея под рукой библиотеку триангуляции Делоне, алгоритм выглядит так:

Чтобы инициализировать,

• Создать набор точек
• Набор точек триангуляции
• Выберите случайную вершину из триангуляции ()

Затем цикл:

• Выберите случайное ребро, соединенное с последней посещенной вершиной, только если другая вершина, соединенная с ребром, еще не была посещена (это ребро является следующим сегментом)
• Отметьте вершину, из которой мы только что пришли, как посещенную
• lastVisitedVertex = другая вершина выбранного ребра
• Повторите цикл снова или выйдите, если длина пути превышает желаемую длину (т.е.> 25)

Иллюстрации

Случайные пути на триангулированном множестве точек диска Пуассона

[

Случайные пути на триангулированном наборе случайных точек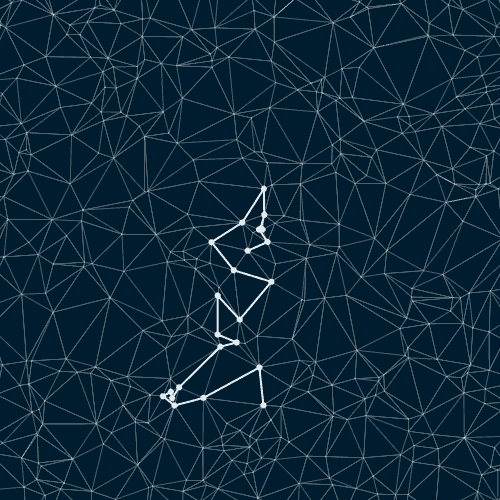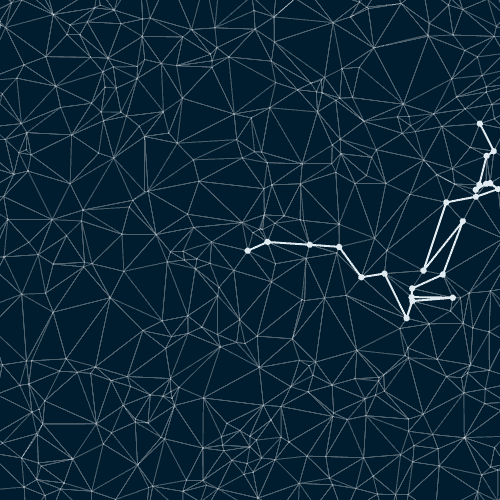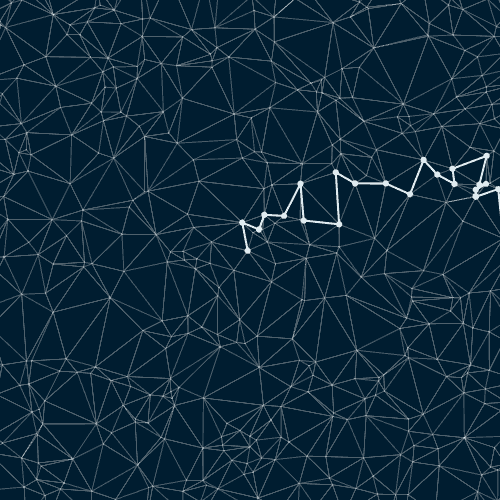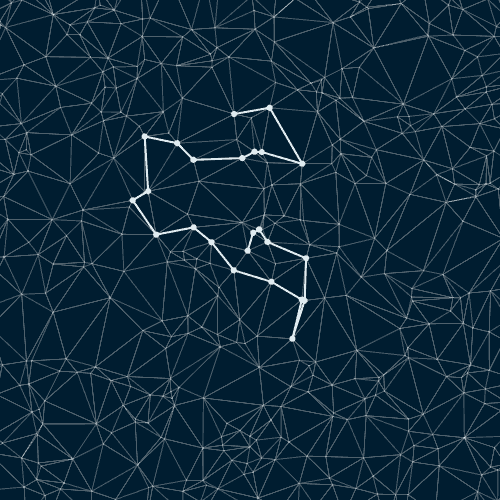

Код

Вот пример использования библиотеки Tinfour для триангуляции на Java . При использовании библиотеки для триангуляции я советую вам выбрать ту, которая обеспечивает легкий доступ к связанным ребрам для данной вершины и вершинам, составляющим данное ребро.

В этом примере я выбираю случайное ребро (а не вершину) в качестве отправной точки.

      ArrayList<Vertex> randomPath(List<Vertex> randomPoints, int pathLength) {

    IncrementalTin tin = new IncrementalTin(10);

    tin.add(randomPoints, null); // insert point set; points are triangulated upon insertion

    HashSet<Vertex> visitedVertices = new HashSet<>();
    ArrayList<Vertex> pathVertices = new ArrayList<>();

    IQuadEdge lastEdge = tin.getStartingEdge(); // get random edge

    int n = 0;
    while (n <= pathLength) {

        List<IQuadEdge> list = new ArrayList<>();
        lastEdge.pinwheel().forEach(list::add); // get edges connected to A; add to array
        IQuadEdge nextEdge;
        int attempts = 0;
        do {
            nextEdge = list.get(random.nextInt(list.size())); // randomly select connected edge
            if (attempts++ > list.size() * 4) {
                return pathVertices; // path ended prematurely (no possible edges to take)
            }
        } while (visitedVertices.contains(nextEdge.getB()) || nextEdge.getB() == null);

        lastEdge = nextEdge.getDual(); // A and B flip around, so A is next vertex
        pathVertices.add(lastEdge.getB()); // add the point we just came from to path
        visitedVertices.add(lastEdge.getB()); // add the point we just came from to visited vertices
        n++;
    }
    return pathVertices;
}