Как найти сильно связанные компоненты в графике?

Question

Я пытаюсь самостоятельно изучить теорию графов, и теперь пытаюсь понять, как найти SCC в графе. Я прочитал несколько разных вопросов / ответов по SO (например, 1, 2, 3, 4, 5, 6, 7, 8), но я не могу найти один с полным пошаговым примером, которому я мог бы следовать.

Согласно CORMEN (Введение в алгоритмы), один метод:

1. Вызовите DFS(G), чтобы вычислить время окончания f[u] для каждой вершины u
2. Вычислить транспонировать (G)
3. Вызовите DFS(Transpose(G)), но в основном цикле DFS рассмотрите вершины в порядке убывания f[u] (как вычислено в шаге 1)
4. Выведите вершины каждого дерева в лесе глубины первый шага 3 как отдельный компонент со строгой связью

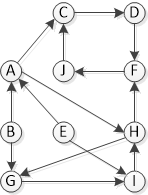
Обратите внимание на следующий график (вопрос 3.4 здесь. Я нашел несколько решений здесь и здесь, но я пытаюсь разбить это и понять сам).

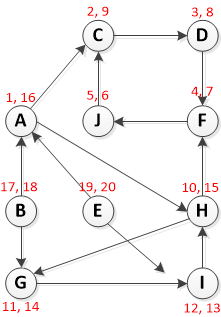
Шаг 1: Вызовите DFS(G), чтобы вычислить время окончания f[u] для каждой вершины u

Запуск DFS, начиная с вершины A:

Обратите внимание на красный текст, отформатированный как [Pre-Vist, Post-Visit]

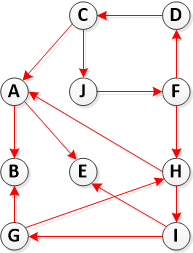
Шаг 2: Вычислить транспонирование (G)

Шаг 3. Вызовите DFS(Transpose(G)), но в главном цикле DFS рассмотрите вершины в порядке убывания f[u] (как вычислено в шаге 1)

Итак, вершины в порядке уменьшения значений после посещения (время окончания):

{E, B, A, H, G, I, C, D, F, J}

Итак, на этом шаге мы запускаем DFS на G^T, но начинаем с каждой вершины из списка выше:

• DFS (E): {E}
• DFS (B): {B}
• DFS (A): {A}
• DFS (H): {H, I, G}
• DFS(G): удалить из списка, так как он уже посещен
• DFS(I): удалить из списка, поскольку он уже посещен
• DFS (C): {C, J, F, D}
• DFS (J): удалить из списка, поскольку он уже посещен
• DFS (F): удалить из списка, поскольку он уже посещен
• DFS (D): удалить из списка, так как он уже посещен

Шаг 4: Выведите вершины каждого дерева в лесе глубины первого шага 3 как отдельный компонент с сильной связью.

Итак, у нас есть пять сильно связанных компонентов: {E}, {B}, {A}, {H, I, G}, {C, J, F, D}

Это то, что я считаю правильным. Однако решения, которые я нашел здесь и здесь, говорят, что SCC - это {C,J,F,H,I,G,D} и {A,E,B}. Где мои ошибки?

Answer 1

Ваши шаги верны, и ваш ответ также верен. Изучив другие предоставленные вами ответы, вы увидите, что они использовали другой алгоритм: сначала вы запускаете DFS на транспонированном G, а затем запускаете алгоритм неориентированных компонентов на G, обрабатывающий вершины по убыванию порядок их почтовых номеров из предыдущего шага.

Проблема в том, что они выполнили этот последний шаг на G транспонированной вместо G и, таким образом, получили неверный ответ. Если вы прочитаете Dasgupta со страницы 98 и далее, вы увидите подробное объяснение алгоритма, который они (пытались) использовать.

Answer 2

Ваши ответы верны. Согласно CLRS, "сильно связная компонента ориентированного графа G = (V,E) является максимальным набором вершин C, так что для каждой пары вершин u и v мы имеем и u ~> v, и v ~> u, то есть вершины v и u достижимы друг от друга."

В случае, если вы принимаете {C, J, F, H, I, G, D} как правильное, нет никакого способа достичь от D до G (среди многих других ошибок), и то же самое с другим набором, нет никакого способа добраться от А до Е.