Нахождение сильно связанных компонентов в графе через DFS

Question

Я читал графические алгоритмы о BFS и DFS. Когда я анализировал алгоритм нахождения сильно связанного компонента в Графике через DFS, у меня возникло сомнение. Для нахождения сильно связанного компонента, что делает книга (Coremen), сначала она запустила DFS на графе, чтобы получить время окончания вершин, затем снова запустила DFS для транспонирования графа в порядке убывания времени окончания. который мы получили из первого DFS. Но я не могу понять, почему второй DFS должен быть запущен в соответствии с временем окончания. Я имею в виду, что даже если мы напрямую запустим DFS (игнорируя время окончания) для транспонирования графа, он мог бы также дать нам подключенные компоненты, потому что, выполняя транспонирование, мы уже заблокировали путь к другим компонентам.

Answer 1

Edit- Вот несколько хороших подробных видео из Стэнфордского университета на эту тему:

http://openclassroom.stanford.edu/MainFolder/CoursePage.php?course=IntroToAlgorithms (см. 6. СОЕДИНЕНИЕ В НАПРАВЛЕННЫХ ГРАФАХ)

Мое объяснение:

Возможно, что вы неправильно определили бы весь граф как один сильно связанный компонент (SCC), если вы не запускаете второй dfs в соответствии с уменьшением времени окончания первого dfs.

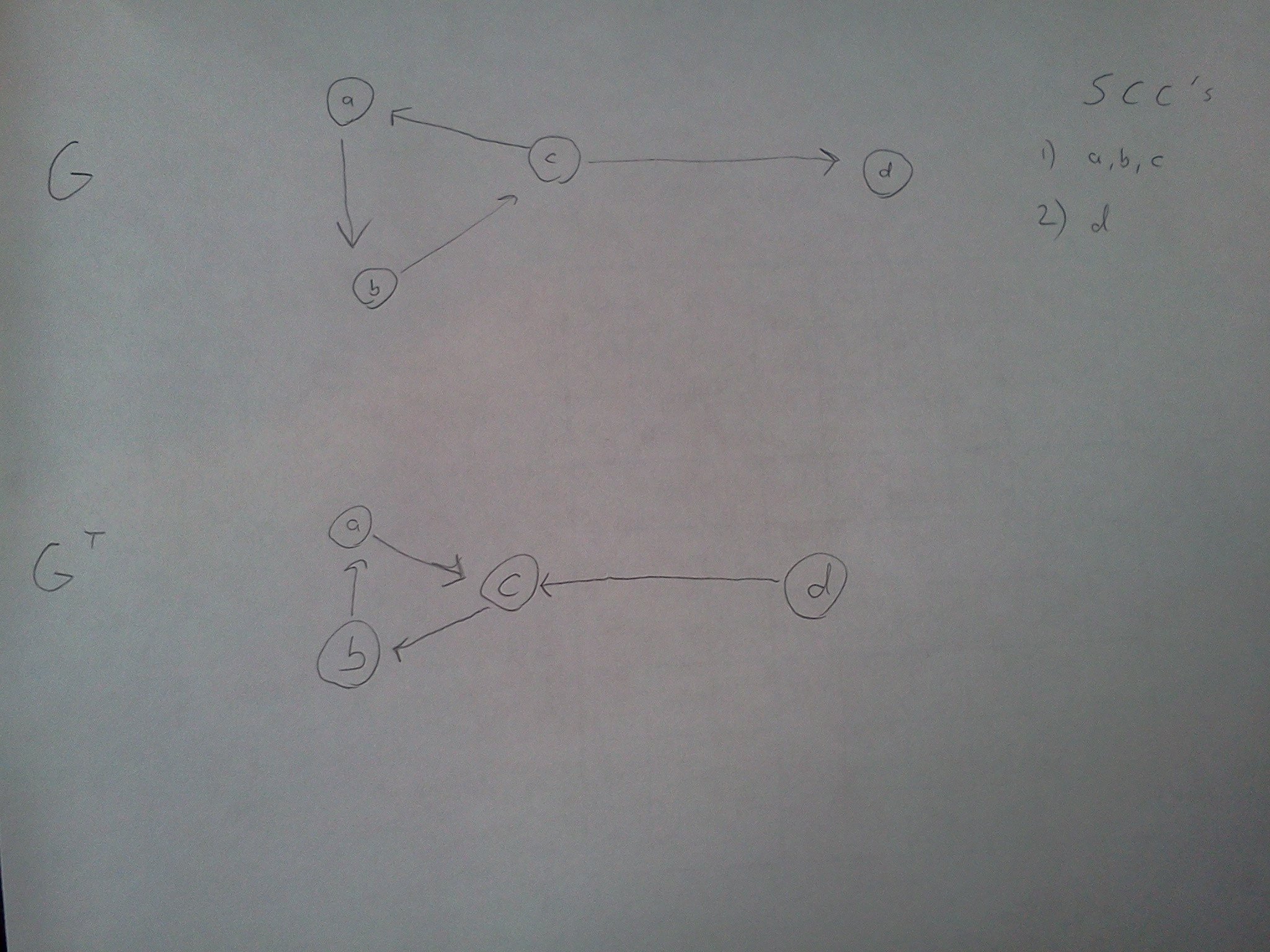
Обратите внимание, что в моем примере узел d всегда будет иметь самое низкое время финиша с первого раза. Один из узлов a, b, или же c будет иметь самые высокие времена финиша. Давайте предположим, a имеет самое высокое время финиша, и поэтому, если мы запустили второй DFS в соответствии с уменьшением времени финиша, a будет первым.

Теперь, если вы запустили второй DFS, начиная с узла d в транспонировании G, вы бы создали первый лес глубины, содержащий весь граф, и, таким образом, пришли к выводу, что весь граф является SCC, что явно неверно. Тем не менее, если вы начинаете DFS с aтогда вы не только откроете для себя a, b, а также cкак SCC, но важная часть заключается в том, что они будут отмечены как посещенные серым или черным цветом. Затем, когда вы продолжаете DFS на dвы бы не вышли из его SCC, потому что поняли бы, что его соседние узлы были посещены.

Если вы посмотрите на код cormens для DFS,

DFS(G)
1 for each vertex u in G.V
2     u.color = WHITE
3     u.π = NIL
4 time = 0
5 for each vertex u in G.V
6     if u.color == WHITE
7         DFS-VISIT(G, u)

DFS-VISIT(G, u)
1 time = time + 1 // white vertex u has just been discovered
2 u.d = time
3 u.color = GRAY
4 for each v in G.adj[u]
5     if v.color == WHITE
6         v.π = u
7         DFS-VISIT(G, u)
8 u.color = BLACK // blacken u; it is finished
9 time = time + 1
10 u.f = time

если бы вы не использовали уменьшение времени окончания, тогда строка 6 DFS была бы истинной только один раз, потому что DFS-VISIT рекурсивно посещал бы весь граф. Это создает одно дерево в глубине первого леса, и каждое дерево является SCC. Причина для отдельного дерева состоит в том, что дерево идентифицируется его корневым узлом, имеющим нулевой предшественник.