Как интерпретировать оценки коэффициента lm() при использовании функции bs() для сплайнов

Question

Я использую набор точек, которые идут от (-5,5) в (0,0) а также (5,5) в "симметричной V-образной форме". Я подгоняю модель с lm() и bs() Функция для подгонки V-образного сплайна:

lm(formula = y ~ bs(x, degree = 1, knots = c(0)))

Я получаю V-образную форму, когда прогнозирую predict() и нарисуйте линию предсказания. Но когда я смотрю на оценки модели coef()Я вижу оценки, которые я не ожидаю.

Coefficients:
                                 Estimate Std. Error t value Pr(>|t|)  
(Intercept)                       4.93821    0.16117  30.639 1.40e-09 ***
bs(x, degree = 1, knots = c(0))1 -5.12079    0.24026 -21.313 2.47e-08 ***
bs(x, degree = 1, knots = c(0))2 -0.05545    0.21701  -0.256    0.805 

Я бы ожидал -1 Коэффициент для первой части и +1 Коэффициент для второй части. Должен ли я интерпретировать оценки по-другому?

Если я заполню узел в lm() Работаем вручную, чем получаю эти коэффициенты:

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.18258    0.13558  -1.347    0.215    
x           -1.02416    0.04805 -21.313 2.47e-08 ***
z            2.03723    0.08575  23.759 1.05e-08 ***

Это больше походит на это. Относительное изменение Z (точки узла) к x составляет ~ +1

Я хочу понять, как интерпретировать bs() результат. Я проверил, руководство и bs Значения предсказания модели точно такие же.

Answer 1

Я бы ожидал -1 Коэффициент для первой части и +1 Коэффициент для второй части.

Я думаю, что ваш вопрос действительно о том, что такое функция B-сплайна. Если вы хотите понять значение коэффициентов, вам нужно знать, какие базисные функции предназначены для вашего сплайна. Смотрите следующее:

library(splines)
x <- seq(-5, 5, length = 100)
b <- bs(x, degree = 1, knots = 0)  ## returns a basis matrix
str(b)  ## check structure
b1 <- b[, 1]  ## basis 1
b2 <- b[, 2]  ## basis 2
par(mfrow = c(1, 2))
plot(x, b1, type = "l", main = "basis 1: b1")
plot(x, b2, type = "l", main = "basis 2: b2")

Замечания:

1. B-сплайны степени 1 - это функции палатки, как вы можете видеть из b1;
2. B-сплайны степени 1 масштабируются, так что их функциональное значение находится между (0, 1);
3. узлы B-сплайна степени-1 - это то место, где он изгибается;
4. B-сплайны степени-1 компактны и являются ненулевыми по трем (не более) трем соседним узлам.

Вы можете получить (рекурсивное) выражение B-сплайнов из определения B-сплайна. B-сплайн степени 0 является наиболее базовым классом, в то время как

• B-сплайн степени 1 является линейной комбинацией B-сплайна степени 0
• B-сплайн степени 2 является линейной комбинацией B-сплайна степени 1
• B-сплайн степени 3 является линейной комбинацией B-сплайна степени 2

(Извините, я получаю не по теме...)

Ваша линейная регрессия с использованием B-сплайнов:

y ~ bs(x, degree = 1, knots = 0)

просто делает:

y ~ b1 + b2

Теперь вы должны понимать, какой коэффициент вы имеете в виду, это означает, что функция сплайна:

-5.12079 * b1 - 0.05545 * b2

В сводной таблице:

Coefficients:
                                 Estimate Std. Error t value Pr(>|t|)  
(Intercept)                       4.93821    0.16117  30.639 1.40e-09 ***
bs(x, degree = 1, knots = c(0))1 -5.12079    0.24026 -21.313 2.47e-08 ***
bs(x, degree = 1, knots = c(0))2 -0.05545    0.21701  -0.256    0.805 

Вы можете спросить, почему коэффициент b2 не имеет значения. Ну сравни свои y а также b1: Ваш y симметричная V-образная форма, в то время как b1 обратная симметричная V-образная форма. Если вы сначала умножить -1 в b1и измените его масштаб, умножив 5, (это объясняет коэффициент -5 за b1), что вы получаете? Хороший матч, верно? Так что нет необходимости b2,

Однако, если ваш y асимметричный, беговой желоб (-5,5) в (0,0)затем (5,10), тогда вы заметите, что коэффициенты для b1 а также b2 оба значимы. Я думаю, что другой ответ уже дал вам такой пример.

---

Репараметризация подогнанного B-сплайна до кусочно-полиномиального демонстрируется здесь: Перепараметризовать подогнанный сплайн-регрессию как кусочно-полиномиальные и экспортные полиномиальные коэффициенты.

Answer 2

Простой пример сплайна первой степени с одним узлом и интерпретацией оценочных коэффициентов для расчета наклона подогнанных линий:

library(splines)
set.seed(313)
x<-seq(-5,+5,len=1000)
y<-c(seq(5,0,len=500)+rnorm(500,0,0.25),
     seq(0,10,len=500)+rnorm(500,0,0.25))
plot(x,y, xlim = c(-6,+6), ylim = c(0,+8))
fit <- lm(formula = y ~ bs(x, degree = 1, knots = c(0)))
x.predict <- seq(-2.5,+2.5,len = 100)
lines(x.predict, predict(fit, data.frame(x = x.predict)), col =2, lwd = 2)

производит сюжет 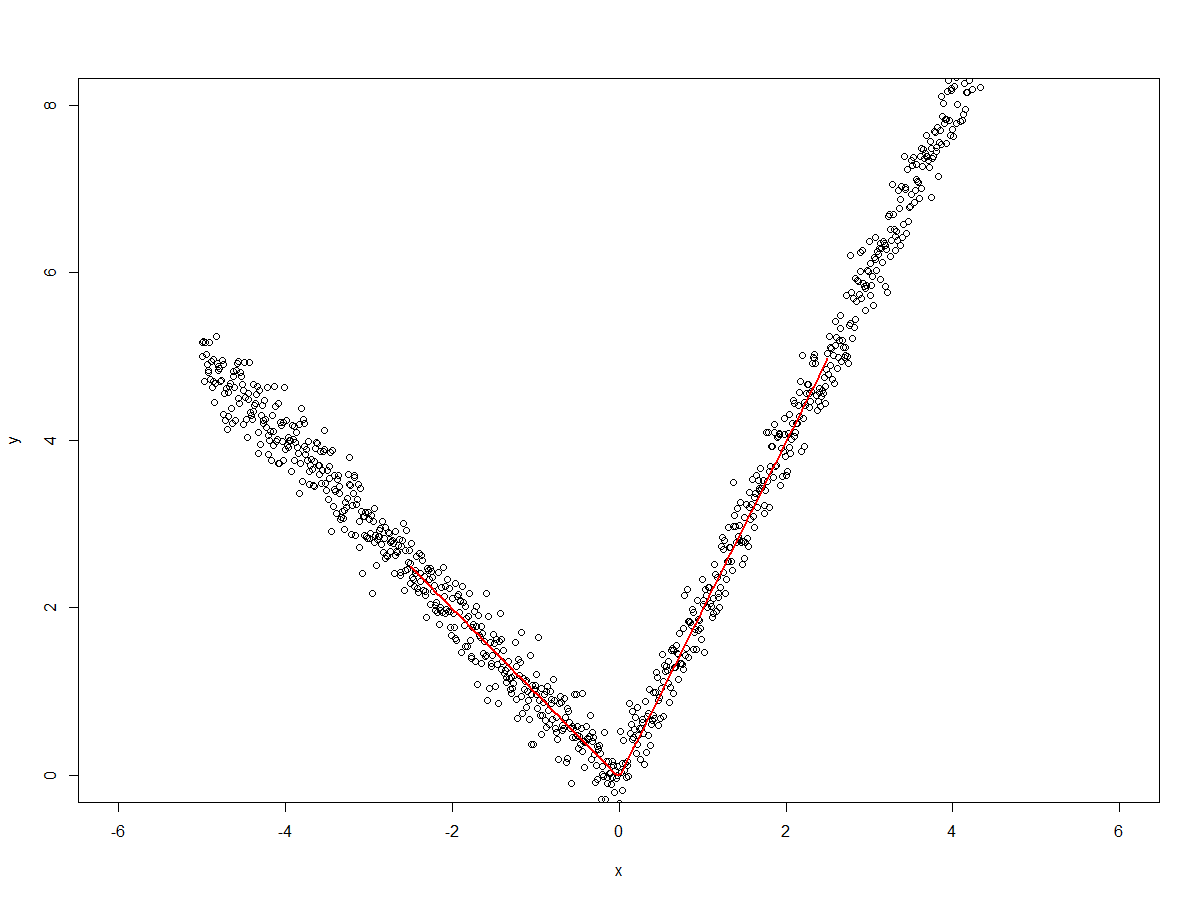Так как мы подгоняем сплайн с degree=1 (то есть прямая линия) и с узлом в x=0у нас есть две строки для x<=0 а также x>0,

Коэффициенты

> round(summary(fit)$coefficients,3)
                                 Estimate Std. Error  t value Pr(>|t|)
(Intercept)                         5.014      0.021  241.961        0
bs(x, degree = 1, knots = c(0))1   -5.041      0.030 -166.156        0
bs(x, degree = 1, knots = c(0))2    4.964      0.027  182.915        0

Который может быть переведен в уклоны для каждой прямой линии, используя узел (который мы указали в x=0) и граничные узлы (мин / макс пояснительных данных):

# two boundary knots and one specified
knot.boundary.left <- min(x)
knot <- 0
knot.boundary.right <- max(x)

slope.1 <- summary(fit)$coefficients[2,1] /(knot - knot.boundary.left)
slope.2 <- (summary(fit)$coefficients[3,1] - summary(fit)$coefficients[2,1]) / (knot.boundary.right - knot)
slope.1
slope.2
> slope.1
[1] -1.008238
> slope.2
[1] 2.000988