Внедрение Quadtree в Mathematica
Я реализовал квадродерево в Mathematica. Я новичок в кодировании на функциональном языке программирования, таком как Mathematica, и мне было интересно, смогу ли я улучшить это или сделать его более компактным за счет лучшего использования шаблонов.
(Я понимаю, что, возможно, я мог бы оптимизировать дерево, обрезая неиспользуемые узлы, и могли бы быть более эффективные структуры данных, такие как деревья kd для пространственной декомпозиции.)
Кроме того, мне все еще не нравится идея копировать все дерево / выражение каждый раз, когда добавляется новая точка. Но я понимаю, что оперирование выражением в целом, а не изменение частей - это функциональный способ программирования. Буду признателен за любые разъяснения по этому аспекту.
М.В.
Код
ClearAll[qtMakeNode, qtInsert, insideBox, qtDraw, splitBox, isLeaf, qtbb, qtpt];
(* create a quadtree node *)
qtMakeNode[{{xmin_,ymin_}, {xmax_, ymax_}}] :=
{{}, {}, {}, {}, qtbb[{xmin, ymin}, {xmax, ymax}], {}}
(* is pt inside box? *)
insideBox[pt_, bb_] := If[(pt[[1]] <= bb[[2, 1]]) && (pt[[1]] >= bb[[1, 1]]) &&
(pt[[2]] <= bb[[2, 2]]) && (pt[[2]] >= bb[[1, 2]]),
True, False]
(* split bounding box into 4 children *)
splitBox[{{xmin_,ymin_}, {xmax_, ymax_}}] := {
{{xmin, (ymin+ymax)/2}, {(xmin+xmax)/2, ymax}},
{{xmin, ymin},{(xmin+xmax)/2,(ymin+ymax)/2}},
{{(xmin+xmax)/2, ymin},{xmax, (ymin+ymax)/2}},
{{(xmin+xmax)/2, (ymin+ymax)/2},{xmax, ymax}}
}
(* is node a leaf? *)
isLeaf[qt_] := If[ And @@((# == {})& /@ Join[qt[[1;;4]], {List @@ qt[[6]]}]),True, False]
(*--- insert methods ---*)
(* qtInsert #1 - return input if pt is out of bounds *)
qtInsert[qtree_, pt_] /; !insideBox[pt, List @@ qtree[[5]]]:= qtree
(* qtInsert #2 - if leaf, just add pt to node *)
qtInsert[qtree_, pt_] /; isLeaf[qtree] :=
{qtree[[1]],qtree[[2]],qtree[[3]],qtree[[4]],qtree[[5]], qtpt @@ pt}
(* qtInsert #3 - recursively insert pt *)
qtInsert[qtree_, pt_] :=
Module[{cNodes, currPt},
cNodes = qtree[[1;;4]];
(* child nodes not created? *)
If[And @@ ((# == {})& /@ cNodes),
(* compute child node bounds *)
(* create child nodes with above bounds*)
cNodes = qtMakeNode[#]& /@ splitBox[List @@ qtree[[5]]];
];
(* move curr node pt (if not empty) into child *)
currPt = List @@ qtree[[6]];
If[currPt != {},
cNodes = qtInsert[#, currPt]& /@ cNodes;
];
(* insert new pt into child *)
cNodes = qtInsert[#, pt]& /@ cNodes;
(* return new quadtree *)
{cNodes[[1]],cNodes[[2]], cNodes[[3]], cNodes[[4]], qtree[[5]], {}}
]
(* draw quadtree *)
qtDraw[qt_] := Module[{pts, bboxes},
pts = Cases[qt, _qtpt, Infinity] /. qtpt :> List;
bboxes = Cases[qt, _qtbb, Infinity] /. qtbb :> List;
Graphics[{
EdgeForm[Black],Hue[0.2], Map[Disk[#, 0.01]&, pts],
Hue[0.7],EdgeForm[Red], FaceForm[],(Rectangle @@ #) & /@ bboxes
},
Frame->True
]
]
использование
Clear[qt];
len = 50;
pts = RandomReal[{0, 2}, {len, 2}];
qt = qtMakeNode[{{0.0, 0.0}, {2.0, 2.0}}];
Do[qt = qtInsert[qt, pts[[i]]], {i, 1, len}]
qtDraw[qt]
Выход
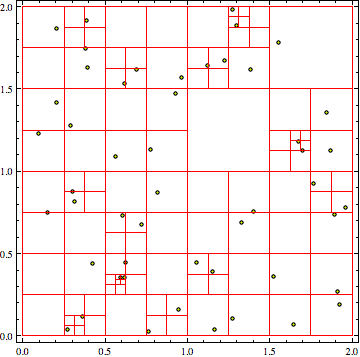
3 ответа
Вот более компактная версия. Он использует ту же структуру данных, что и оригинальная версия. Функции splitBox а также insideBox по сути то же самое (просто написано немного по-другому).
Вместо того, чтобы добавлять точки один за другим, начальное поле содержит все точки в начале, поэтому нет необходимости qtInsert Подпрограммы. На каждом шаге рекурсии поля, содержащие более одной точки, разделяются, а точки распределяются по подполям. Это означает, что все узлы с более чем одной точкой являются листами, поэтому проверять это тоже не нужно.
qtMakeNode[bb_, pts_] := {{}, {}, {}, {}, qtbb @@ bb, pts}
splitBox[bx_] := splitBox[{min_, max_}] := {min + #, max + #}/2 & /@
Tuples[Transpose[{min, max}]]
insideBox[pt_, bb_] := bb[[1, 1]] <= pt[[1]] <= bb[[2, 1]] &&
bb[[1, 2]] <= pt[[2]] <= bb[[2, 2]]
distribute[qtree_] := Which[
Length[qtree[[6]]] == 1,
(* no points in node -> return node unchanged *)
qtree,
Length[qtree[[6]]] == 1,
(* one point in node -> replace head of point with qtpt and return node *)
ReplacePart[qtree, 6 -> qtpt @@ qtree[[6, 1]]],
Length[qtree[[6]]] > 1,
(* multiple points in node -> create sub-nodes and distribute points *)
(* apply distribute to sub-nodes *)
Module[{spl = splitBox[qtree[[5]]], div, newtreelist},
div = Cases[qtree[[6]], a_ /; insideBox[a, #], 1] & /@ spl;
ReplacePart[qtree,
Join[Table[i -> distribute[qtMakeNode[spl[[i]], div[[i]]]], {i, 4}],
{6 -> {}}]]]]
Пример (с использованием оригинальной версии qtDraw):
len = 50;
pts = RandomReal[{0, 2}, {len, 2}];
qt = makeTree[qtMakeNode[{{0.0, 0.0}, {2.0, 2.0}}, pts]];
qtDraw[qt]
Результат:
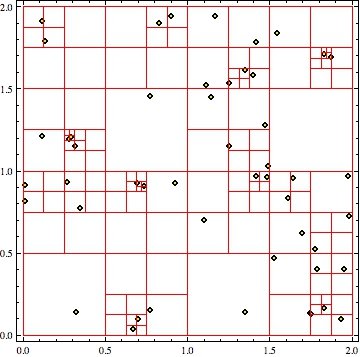
Я думаю, что ваш код не так требователен к памяти, как вы могли ожидать. Он ломает и реформирует списки, но, как правило, сохраняет большинство списков нетронутыми.
Как отмечали другие, возможно, можно было бы добиться большего успеха, используя атрибуты Hold-обертки и / или HoldXXX, чтобы эмулировать вызов по ссылке.
Для жесткого подхода к некоторым связанным реализациям структуры данных, см.
http://library.wolfram.com/infocenter/MathSource/7619/
Соответствующий код находится в записной книжке Hemmecke-final.nb (названной так, потому что он реализует торический базисный алгоритм Гребнера благодаря Р. Хеммеке и соавторам).
Я попытался переопределить использование атрибутов Hold..., но я не очень хорош в этом и отказался, когда код получил ответный удар (пропустил, но убил мой сеанс Mathematica). Поэтому вместо этого у меня есть реализация, которая использует недокументированный "сырой" тип данных Mathematica, который является инертным и, следовательно, поддается поведению по ссылке.
Рассматриваемая структура называется "мешок expr", потому что общая структура данных Mathematica - это "expr". Он похож на список, но (1) он может расти с одной стороны (но не сжиматься) и (2) как другие необработанные типы выражений (например, графики в версии 8), имеет компоненты, к которым можно обращаться и / или изменять с помощью предоставленных функций (API, так сказать). Его базовые "элементы" инертны в том смысле, что они могут ссылаться на ЛЮБОЙ expr (включая саму сумку), и ими можно манипулировать способами, которые я укажу ниже.
Первый пункт выше предоставляет основную технологию для внедрения Sow/Reap. Это второе, что будет интересно в приведенном ниже коде. В конце я добавлю несколько замечаний по объяснению структуры данных, поскольку для этого нет официальной документации.
Я сохранил код более или менее в том же стиле, что и оригинал, и, в частности, он остается онлайн-версией (то есть элементы не обязательно должны входить в начало, но могут быть добавлены по отдельности). Поменял несколько имен. Сделал базовую структуру сродни
узел (ограничивающий прямоугольник, значение, ноль или четыре подузла)
Если есть подузлы, то поле значения будет пустым. Поля box и value представлены обычным выражением Mathematica List, хотя, возможно, имеет смысл использовать выделенные заголовки и делать их более похожими на стиль структуры C. Я сделал что-то подобное в названии различных функций доступа / настройки полей.
Одно предостережение заключается в том, что этот тип необработанных данных потребляет значительно больше памяти, чем, например, список. Так что мой вариант ниже будет использовать больше памяти, чем первоначально размещенный код. Не асимптотически больше, просто постоянным фактором. Кроме того, он требует постоянного фактора в накладных расходах больше, чем, скажем, сопоставимая структура C с точки зрения доступа или установки значения элемента. Так что это не волшебная палочка, просто тип данных с поведением, которое не должно вызывать асимптотических сюрпризов.
AppendTo[$ContextPath, "Internal`"];
makeQuadTreeNode[bounds_] := Bag[{bounds, {}, {}}]
(*is pt inside box?*)
insideBox[pt_, box_] :=
And @@ Thread[box[[1]] <= (List @@ pt) <= box[[2]]]
(*split bounding box into 4 children*)
splitBox[{{xmin_, ymin_}, {xmax_, ymax_}}] :=
Map[makeQuadTreeNode, {{{xmin, (ymin + ymax)/2}, {(xmin + xmax)/2,
ymax}}, {{xmin,
ymin}, {(xmin + xmax)/2, (ymin + ymax)/2}}, {{(xmin + xmax)/2,
ymin}, {xmax, (ymin + ymax)/2}}, {{(xmin + xmax)/
2, (ymin + ymax)/2}, {xmax, ymax}}}]
bounds[qt_] := BagPart[qt, 1]
value[qt_] := BagPart[qt, 2]
children[qt_] := BagPart[qt, 3]
isLeaf[qt_] := value[qt] =!= {}
isSplit[qt_] := children[qt] =!= {}
emptyNode[qt_] := ! isLeaf[qt] && ! isSplit[qt]
(*qtInsert #1-return input if pt is out of bounds*)
qtInsert[qtree_, pt_] /; ! insideBox[pt, bounds[qtree]] := qtree
(*qtInsert #2-empty node (no value,no children)*)
qtInsert[qtree_, pt_] /; emptyNode[qtree] := value[qtree] = pt
(*qtInsert #2-currently a leaf (has a value and no children)*)
qtInsert[qtree_, pt_] /; isLeaf[qtree] := Module[
{kids = splitBox[bounds[qtree]], currval = value[qtree]},
value[qtree] = {};
children[qtree] = kids;
Map[(qtInsert[#, currval]; qtInsert[#, pt]) &, kids];
]
(*qtInsert #4-not a leaf and has children*)
qtInsert[qtree_, pt_] := Map[qtInsert[#, pt] &, children[qtree]];
getBoxes[ee_Bag] :=
Join[{bounds[ee]}, Flatten[Map[getBoxes, children[ee]], 1]]
getPoints[ee_Bag] :=
Join[{value[ee]}, Flatten[Map[getPoints, children[ee]], 1]]
qtDraw[qt_] := Module[
{pts, bboxes},
pts = getPoints[qt] /. {} :> Sequence[];
bboxes = getBoxes[qt];
Graphics[{EdgeForm[Black], Hue[0.2], Map[Disk[#, 0.01] &, pts],
Hue[0.7], EdgeForm[Red],
FaceForm[], (Rectangle @@ #) & /@ bboxes}, Frame -> True]]
Вот пример. Отмечу, что масштабирование разумное. Возможно O(n log(n)) или около того. Определенно лучше, чем O(n^2).
len = 4000;
pts = RandomReal[{0, 2}, {len, 2}];
qt = makeQuadTreeNode[{{0.0, 0.0}, {2.0, 2.0}}];
Timing[Do[qtInsert[qt, pts[[i]]], {i, 1, len}]]
{1.6, Null}
Общие примечания к пакету expr. Они старые, поэтому я не утверждаю, что это все еще работает, как указано.
Эти функции живут во внутреннем контексте.
Bag Создает мешок expr, опционально с предустановленными элементами.
BagPart Получает части пакета expr, аналогичные Part для обычных выражений. Также может использоваться на lhs, например, для сброса значения.
StuffBag Добавляет элементы в конец сумки.
У нас также есть BagLength. Полезно для перебора по сумке.
Эти функции чрезвычайно полезны по двум причинам.
Во-первых, это хороший способ создать расширяемую таблицу в Mathematica.
Во-вторых, содержимое пакетов оценивается, но затем помещается в исходный текст, следовательно, экранируется. Таким образом, можно использовать их как "указатели" (в смысле C), а не как объекты, и это не требует удержания и т. Д. Вот несколько примеров:
a = {1,2,a} (* gives infinite recursion *)
Если вместо этого мы будем использовать сумки, мы получим структуру со ссылками на себя.
In[1]:= AppendTo[$ContextPath, "Internal`"];
In[2]:= a = Bag[{1,2,a}]
Out[2]= Bag[<3>]
In[3]:= expr1 = BagPart[a, All]
Out[3]= {1, 2, Bag[<3>]}
In[4]:= expr2 = BagPart[BagPart[a, 3], All]
Out[4]= {1, 2, Bag[<3>]}
In[5]:= expr1 === expr2
Out[5]= True
Этому трудно подражать любым другим способом в Mathematica. Можно было бы использовать разреженные таблицы (хеширование) не совсем прозрачным способом.
Вот пример, не полностью отлаженный. Мы в основном реализуем связанный список, с помощью которого можно деструктивно изменять хвосты, заменять подсписки и т. Д.
tail[ll_] := BagPart[ll,2]
settail[ll_, ll2_] := BagPart[ll,2] = ll2
contents[ll_] := BagPart[ll,1]
setcontents[ll_, elem_] := BagPart[ll,1] = elem
createlinkedlist[elems__] := Module[
{result, elist={elems}, prev, el},
result = Bag[{elist[[1]],Bag[]}];
prev = result;
Do [el = Bag[{elist[[j]],Bag[]}];
settail[prev, el];
prev = el,
{j,2,Length[elist]}];
result
]
In[18]:= tt = createlinkedlist[vv,ww,xx]
Out[18]= Bag[<2>]
In[20]:= BagPart[tt,All]
Out[20]= {vv, Bag[<2>]}
Таким образом, tt - это связанный список, первый элемент - это vv, следующий - сам связанный список и т. Д. Я воздержался от использования терминологии Lisp (car/cdr и т. П.), Потому что я не могу вспомнить, являются ли операции со списками Lisp деструктивными. Но вы получите общее представление.
В том же духе я использовал пакеты expr для реализации бинарных деревьев. Это полезно, потому что мы можем вносить деструктивные изменения в постоянное время (при условии, что у нас уже есть "дескриптор" в точке вставки / удаления), и, кроме того, "сырая" природа пакетов expr означает, что мы полностью избегаем бесконечной семантики оценки Mathematica.
Возможно, другое приложение.
Pointer = Internal`Bag
Contents[aa_Pointer, j_Integer] /;0<j<=Internal`BagLength[aa] :=
Internal`BagPart[aa,j]
SetContents[aa_Pointer, j_Integer, e_] /; 0<j<=Internal`BagLength[aa] :=
Internal`BagPart[aa,j] = e
SetContents[aa_Pointer, j_Integer, e_] /; j>BagLength[aa] :=
(Do[Internal`StuffBag[aa,Null], {k,Internal`BagLength[aa]+1,j-1}];
Internal`StuffBag[aa,e])
Попробуй с
a = Bag[{1,2,a,6,t,y,99,Bag[{a,q,3,r,a,5,t}]}]
expr1 = BagPart[a, All]
expr2 = BagPart[BagPart[a, 3], All]
Contents[a, 4]
SetContents[a, 7, Contents[a,7]+5]
SetContents[a,11,33]
Даниэль Лихтблау Вольфрам Исследования
Возможно, это не то, что вы пытаетесь сделать, но Nearest[] может создать функцию NearestFunction[], которая является встроенной структурой дерева квадрантов.