Уменьшение размерности с помощью самоорганизующихся карт

Question

Я работаю над самоорганизующимися картами (SOM) в течение последних нескольких месяцев. Но у меня все еще есть некоторые заблуждения в понимании части сокращения размерностей. Можете ли вы предложить какой-либо простой метод, чтобы понять реальную работу SOM на любых наборах данных реального мира (как набор данных из хранилища UCI).

Answer 1

Итак, прежде всего обратитесь к некоторым предыдущим связанным вопросам, которые помогут вам лучше понять свойства уменьшения размеров и визуализации SOM. Построение карты Кохонена - Понимание визуализации, Интерпретация самоорганизующейся карты.

Второй простой случай для проверки свойств СДЛ:

• Создайте простой набор данных с 3 функциями, где у вас есть 3 разных кластера;
• Выполните SOM для этого набора данных и визуализируйте.

Я буду использовать язык программирования MATLAB, чтобы показать, как это сделать и что вы можете извлечь из процесса обучения.

КОД:

% create a dataset with 3 clusters and 3 features
x=[ones(1000,1)*0.5,zeros(1000,1),zeros(1000,1)]; 
x=[x;[zeros(1000,1),ones(1000,1)*0.5,zeros(1000,1)]]; 
x=[x;[zeros(1000,1),zeros(1000,1),ones(1000,1)*0.5]]; 
x=x+rand(3000,3)*0.2; 
x=x';

%define a 20x20 SOM through MATLAB "selforgmap" function, and train using the "train"
net = selforgmap([20 20]); 
[net,tr] = train(net,x);

%display the number of hits, neighbour distance, and plane maps     figure,plotsomplanes(net)
figure,plotsomnd(net) 

фигура, plotsomhits (чистый, х)

ВЫХОД:

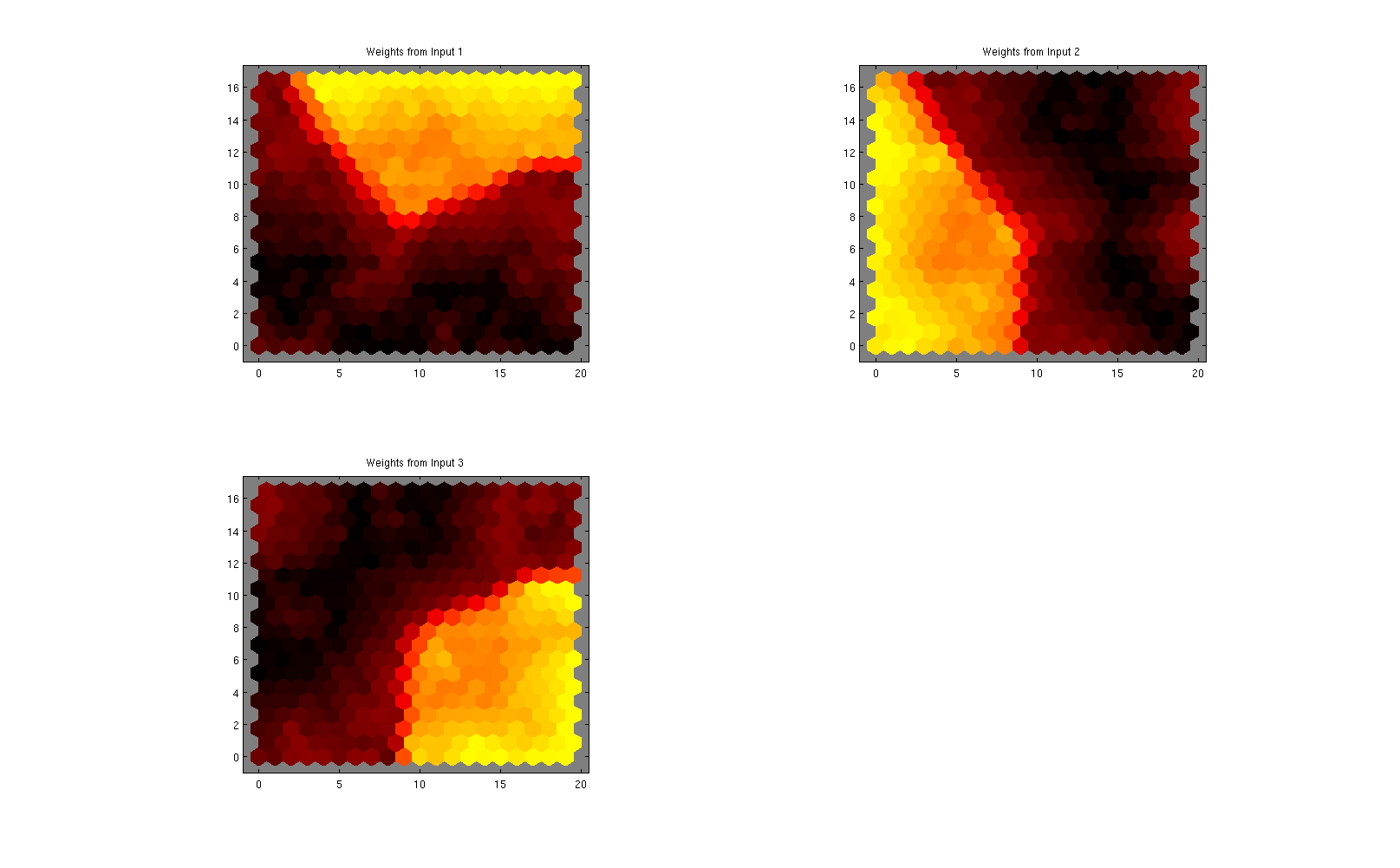
Итак, на первом рисунке вы уже можете увидеть сжатие набора данных 3000x3 в карту 20x20x3 (сокращение почти в 10 раз). Вы также можете видеть, что ваши компоненты могут быть еще более сжаты в 3 отдельных класса.

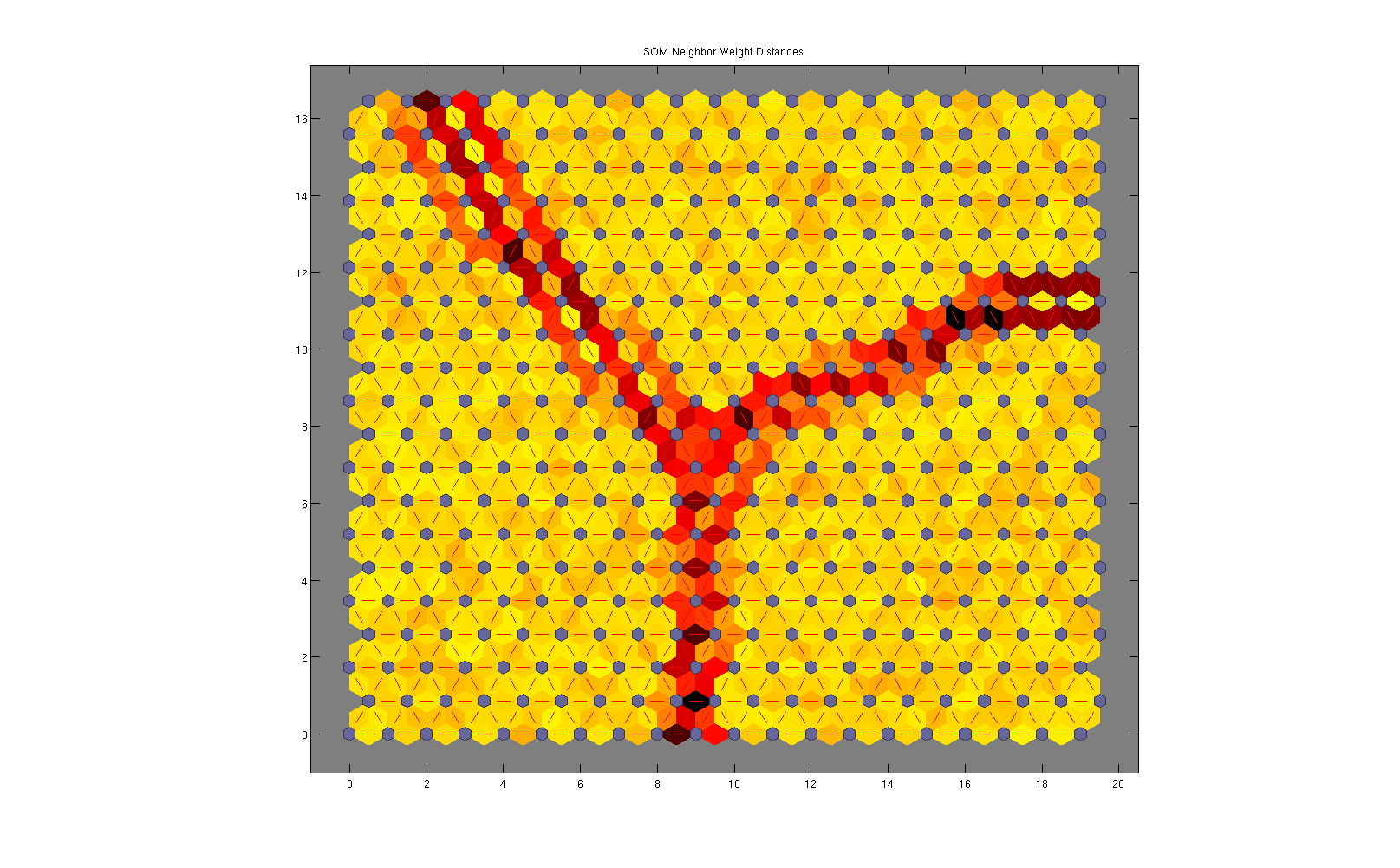
Это становится еще более очевидным, когда вы смотрите на расстояние до соседа и нажимаете на карты (рис. 2 и 3 соответственно):

На рисунке 2 чем больше отличается узел с его соседом (рассчитывается через евклидово расстояние между весами узлов и его весами соседей), тем темнее цвет между этими двумя узлами. Таким образом, мы можем видеть 3 области сильно связанных узлов. Мы могли бы использовать это изображение и пороговое его так, чтобы получить 3 различных региона (3 кластера), а затем получить средние веса.

На рисунке 3 показано, сколько выборок из набора данных где метка в каждом узле. Как можно видеть, в 3 предыдущих областях представлено несколько однородное распределение выборок (что имеет смысл, учитывая, что 3 кластера имеют одинаковое количество выборок), а узлы интерфейса (те, которые разделяют 3 области) не отображаются любой образец. Опять же, мы могли бы использовать это изображение и пороговое его так, чтобы получить 3 различных региона (3 кластера), а затем получить средние веса.

Таким образом, в сумме с этим набором данных и с некоторой легкой последующей обработкой вы можете уменьшить свой набор данных с 3000X3 до матрицы 3x3