Выровнять произвольно повернутые текстовые аннотации относительно текста, а не ограничивающего прямоугольника.
Пытаясь ответить на старый вопрос без ответа, я столкнулся с небольшой проблемой, касающейся текстовых аннотаций в matplotlib: При добавлении повернутого текста к фигуре в определенной позиции текст выравнивается относительно ограничивающего прямоугольника текста, а не (воображаемого) повернутого прямоугольника, в котором содержится сам текст. Это может быть лучше всего объяснено с небольшим примером: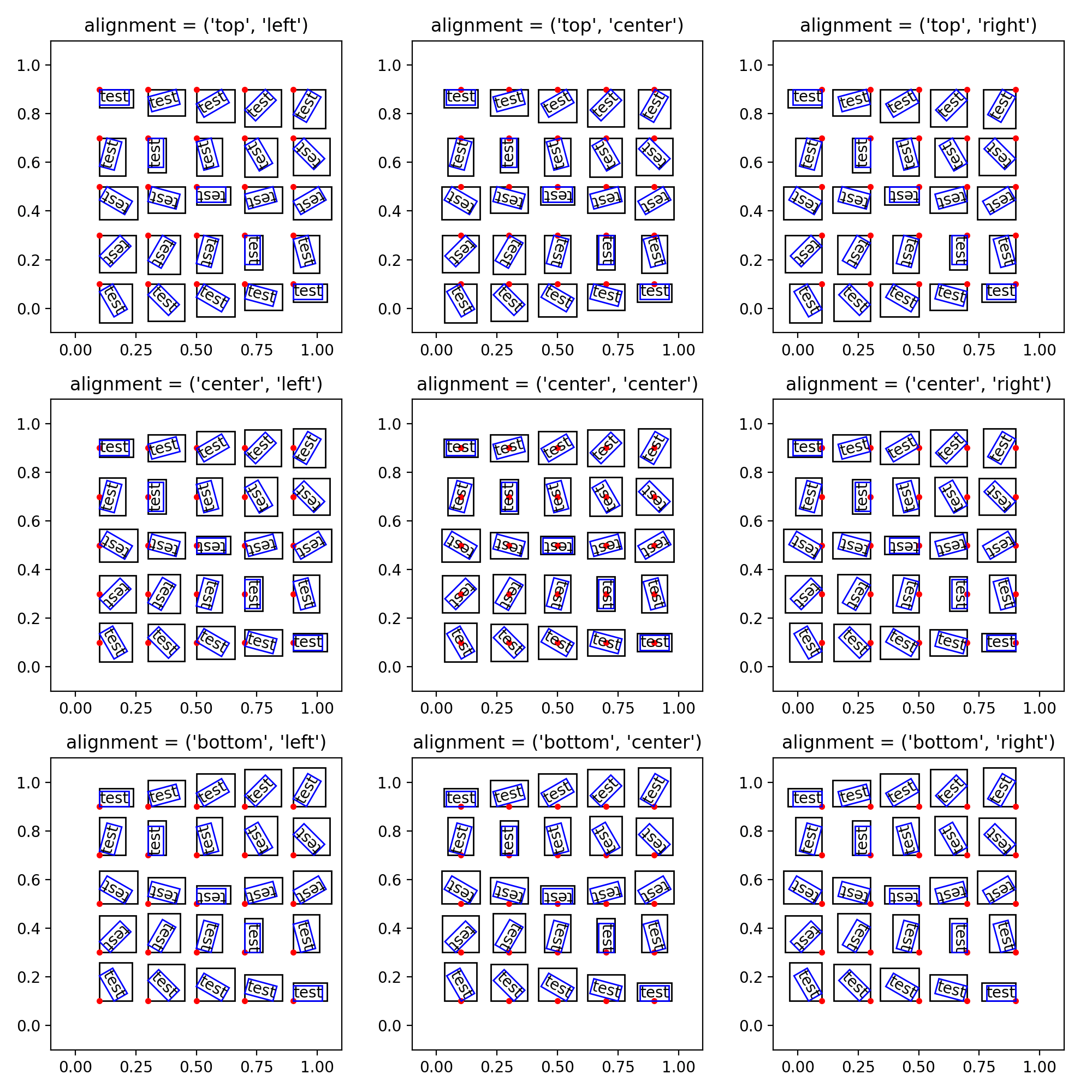 
На рисунке показаны фрагменты текста с разными углами поворота и различными вариантами выравнивания. Для каждого текстового объекта красная точка обозначает координату, данную ax.text() функция. Синяя рамка - это повернутая рамка вокруг текста, а черная рамка - приблизительная ограничительная рамка текста (она слишком большая, но идея должна быть понятна). Легко видеть, что для случаев, когда выравнивание происходит по краям (слева, справа, сверху, снизу), красная точка находится по бокам или по краям ограничительной рамки, а не текстовой рамки. Единственный вариант выравнивания, в котором текст выравнивается интуитивно понятным способом, - это если горизонтальное и вертикальное выравнивание установлено в "центр". Теперь это не ошибка, а предполагаемое поведение, как описано здесь. Однако в некоторых ситуациях это не очень практично, поскольку положение должно быть отрегулировано "вручную", чтобы текст находился в нужном месте, и эта настройка изменяется, если изменяется угол поворота или масштабируется рисунок.
Вопрос в том, существует ли надежный способ создания текста, который выровнен по текстовой рамке, а не по ограничивающей рамке. У меня уже есть решение проблемы, но это было довольно утомительно, поэтому я решил поделиться им.
2 ответа
Новое решение rotation_mode="anchor"
На самом деле есть аргумент rotation_mode в matplotlib.text.Text, который управляет именно требуемой функциональностью. По умолчанию rotation_mode="default" который воссоздает нежелательное поведение из вопроса, в то время как rotation_mode="anchor" закрепляет точку вращения в соответствии с самим текстом, а не с его ограничительной рамкой.
ax.text(x,y,'test', rotation = deg, rotation_mode="anchor")
Также см. Пример demo_text_rotation_mode.
При этом, пример из вопроса может быть легко создан без необходимости подкласса Text,
from matplotlib import pyplot as plt
import numpy as np
fig, axes = plt.subplots(3,3, figsize=(10,10),dpi=100)
aligns = [ (va,ha) for va in ('top', 'center', 'bottom')
for ha in ('left', 'center', 'right')]
xys = [[i,j] for j in np.linspace(0.9,0.1,5) for i in np.linspace(0.1,0.9,5)]
degs = np.linspace(0,360,25)
for ax, align in zip(axes.reshape(-1), aligns):
ax.set_xlim([-0.1,1.1])
ax.set_ylim([-0.1,1.1])
for deg,xy in zip(degs,xys):
x,y = xy
ax.plot(x,y,'r.')
text = ax.text(x,y,'test',
rotation = deg,
rotation_mode="anchor", ### <--- this is the key
va = align[0],
ha = align[1],
bbox=dict(facecolor='none', edgecolor='blue', pad=0.0),
)
ax.set_title('alignment = {}'.format(align))
fig.tight_layout()
plt.show()
старое решение, подкласс Text
Если вам все еще интересно, решение, данное @ThomasKühn, конечно, работает нормально, но имеет некоторые недостатки, когда текст используется в не декартовой системе, потому что он вычисляет смещение, необходимое в координатах данных.
Ниже приведен вариант кода, который смещает текст в координатах отображения с помощью преобразования, которое временно присоединяется при рисовании текста. Поэтому его также можно использовать, например, на полярных участках.
from matplotlib import pyplot as plt
from matplotlib import patches, text
import matplotlib.transforms
import numpy as np
class TextTrueAlign(text.Text):
"""
A Text object that always aligns relative to the text, not
to the bounding box; also when the text is rotated.
"""
def __init__(self, x, y, text, **kwargs):
super(TextTrueAlign, self).__init__(x,y,text, **kwargs)
self.__Ha = self.get_ha()
self.__Va = self.get_va()
def draw(self, renderer, *args, **kwargs):
"""
Overload of the Text.draw() function
"""
trans = self.get_transform()
offset = self.update_position()
# while drawing, set a transform which is offset
self.set_transform(trans + offset)
super(TextTrueAlign, self).draw(renderer, *args, **kwargs)
# reset to original transform
self.set_transform(trans)
def update_position(self):
"""
As the (center/center) alignment always aligns to the center of the
text, even upon rotation, we make use of this here. The algorithm
first computes the (x,y) offset for the un-rotated text between
centered alignment and the alignment requested by the user. This offset
is then rotated by the given rotation angle.
Finally a translation of the negative offset is returned.
"""
#resetting to the original state:
rotation = self.get_rotation()
self.set_rotation(0)
self.set_va(self.__Va)
self.set_ha(self.__Ha)
##from https://stackru.com/questions/5320205/matplotlib-text-dimensions
##getting the current renderer, so that
##get_window_extent() works
renderer = self.axes.figure.canvas.get_renderer()
##computing the bounding box for the un-rotated text
##aligned as requested by the user
bbox1 = self.get_window_extent(renderer=renderer)
##re-aligning text to (center,center) as here rotations
##do what is intuitively expected
self.set_va('center')
self.set_ha('center')
##computing the bounding box for the un-rotated text
##aligned to (center,center)
bbox2 = self.get_window_extent(renderer=renderer)
##computing the difference vector between the two alignments
dr = np.array(bbox2.get_points()[0]-bbox1.get_points()[0])
##computing the rotation matrix, which also accounts for
##the aspect ratio of the figure, to stretch squeeze
##dimensions as needed
rad = np.deg2rad(rotation)
rot_mat = np.array([
[np.cos(rad), np.sin(rad)],
[-np.sin(rad), np.cos(rad)]
])
##computing the offset vector
drp = np.dot(dr,rot_mat)
# transform to translate by the negative offset vector
offset = matplotlib.transforms.Affine2D().translate(-drp[0],-drp[1])
##setting rotation value back to the one requested by the user
self.set_rotation(rotation)
return offset
if __name__ == '__main__':
fig, axes = plt.subplots(3,3, figsize=(10,10),dpi=100)
aligns = [ (va,ha) for va in ('top', 'center', 'bottom')
for ha in ('left', 'center', 'right')]
xys = [[i,j] for j in np.linspace(0.9,0.1,5) for i in np.linspace(0.1,0.9,5)]
degs = np.linspace(0,360,25)
for ax, align in zip(axes.reshape(-1), aligns):
ax.set_xlim([-0.1,1.1])
ax.set_ylim([-0.1,1.1])
for deg,xy in zip(degs,xys):
x,y = xy
ax.plot(x,y,'r.')
text = TextTrueAlign(
x = x,
y = y,
text='test',
axes = ax,
rotation = deg,
va = align[0],
ha = align[1],
bbox=dict(facecolor='none', edgecolor='blue', pad=0.0),
)
ax.add_artist(text)
ax.set_title('alignment = {}'.format(align))
fig.tight_layout()
plt.show()
После некоторого поиска и копания в matplotlib сам код, и с некоторым вдохновением здесь и здесь, я пришел к следующему решению:
from matplotlib import pyplot as plt
from matplotlib import patches, text
import numpy as np
import math
class TextTrueAlign(text.Text):
"""
A Text object that always aligns relative to the text, not
to the bounding box; also when the text is rotated.
"""
def __init__(self, x, y, text, **kwargs):
super().__init__(x,y,text, **kwargs)
self.__Ha = self.get_ha()
self.__Va = self.get_va()
self.__Rotation = self.get_rotation()
self.__Position = self.get_position()
def draw(self, renderer, *args, **kwargs):
"""
Overload of the Text.draw() function
"""
self.update_position()
super().draw(renderer, *args, **kwargs)
def update_position(self):
"""
As the (center/center) alignment always aligns to the center of the
text, even upon rotation, we make use of this here. The algorithm
first computes the (x,y) offset for the un-rotated text between
centered alignment and the alignment requested by the user. This offset
is then transformed according to the requested rotation angle and the
aspect ratio of the graph. Finally the transformed offset is used to
shift the text such that the alignment point coincides with the
requested coordinate also when the text is rotated.
"""
#resetting to the original state:
self.set_rotation(0)
self.set_va(self.__Va)
self.set_ha(self.__Ha)
self.set_position(self.__Position)
ax = self.axes
xy = self.__Position
##determining the aspect ratio:
##from https://stackru.com/questions/41597177/get-aspect-ratio-of-axes
##data limits
xlim = ax.get_xlim()
ylim = ax.get_ylim()
## Axis size on figure
figW, figH = ax.get_figure().get_size_inches()
## Ratio of display units
_, _, w, h = ax.get_position().bounds
##final aspect ratio
aspect = ((figW * w)/(figH * h))*(ylim[1]-ylim[0])/(xlim[1]-xlim[0])
##from https://stackru.com/questions/5320205/matplotlib-text-dimensions
##getting the current renderer, so that
##get_window_extent() works
renderer = ax.figure.canvas.get_renderer()
##computing the bounding box for the un-rotated text
##aligned as requested by the user
bbox1 = self.get_window_extent(renderer=renderer)
bbox1d = ax.transData.inverted().transform(bbox1)
width = bbox1d[1,0]-bbox1d[0,0]
height = bbox1d[1,1]-bbox1d[0,1]
##re-aligning text to (center,center) as here rotations
##do what is intuitively expected
self.set_va('center')
self.set_ha('center')
##computing the bounding box for the un-rotated text
##aligned to (center,center)
bbox2 = self.get_window_extent(renderer=renderer)
bbox2d = ax.transData.inverted().transform(bbox2)
##computing the difference vector between the two
##alignments
dr = np.array(bbox2d[0]-bbox1d[0])
##computing the rotation matrix, which also accounts for
##the aspect ratio of the figure, to stretch squeeze
##dimensions as needed
rad = np.deg2rad(self.__Rotation)
rot_mat = np.array([
[math.cos(rad), math.sin(rad)*aspect],
[-math.sin(rad)/aspect, math.cos(rad)]
])
##computing the offset vector
drp = np.dot(dr,rot_mat)
##setting new position
self.set_position((xy[0]-drp[0],xy[1]-drp[1]))
##setting rotation value back to the one requested by the user
self.set_rotation(self.__Rotation)
if __name__ == '__main__':
fig, axes = plt.subplots(3,3, figsize=(10,10),dpi=100)
aligns = [ (va,ha) for va in ('top', 'center', 'bottom')
for ha in ('left', 'center', 'right')]
xys = [[i,j] for j in np.linspace(0.9,0.1,5) for i in np.linspace(0.1,0.9,5)]
degs = np.linspace(0,360,25)
for ax, align in zip(axes.reshape(-1), aligns):
ax.set_xlim([-0.1,1.1])
ax.set_ylim([-0.1,1.1])
for deg,xy in zip(degs,xys):
ax.plot(*xy,'r.')
text = TextTrueAlign(
x = xy[0],
y = xy[1],
text='test',
axes = ax,
rotation = deg,
va = align[0],
ha = align[1],
bbox=dict(facecolor='none', edgecolor='blue', pad=0.0),
)
ax.add_artist(text)
ax.set_title('alignment = {}'.format(align))
fig.tight_layout()
plt.show()
Пример является довольно длинным, потому что мне пришлось написать класс, производный от matplotlib.text.Text класс для правильного обновления текстового объекта при перерисовке (например, если рисунок масштабируется). Код опирается на текст, всегда выровненный по его центральной точке, если горизонтальное и вертикальное выравнивание установлено в "центр". Требуется различие между ограничительными рамками текста с выравниванием по центру и с запрошенным выравниванием, чтобы предсказать смещение, на которое текст должен быть сдвинут после поворота. Результат примера выглядит следующим образом: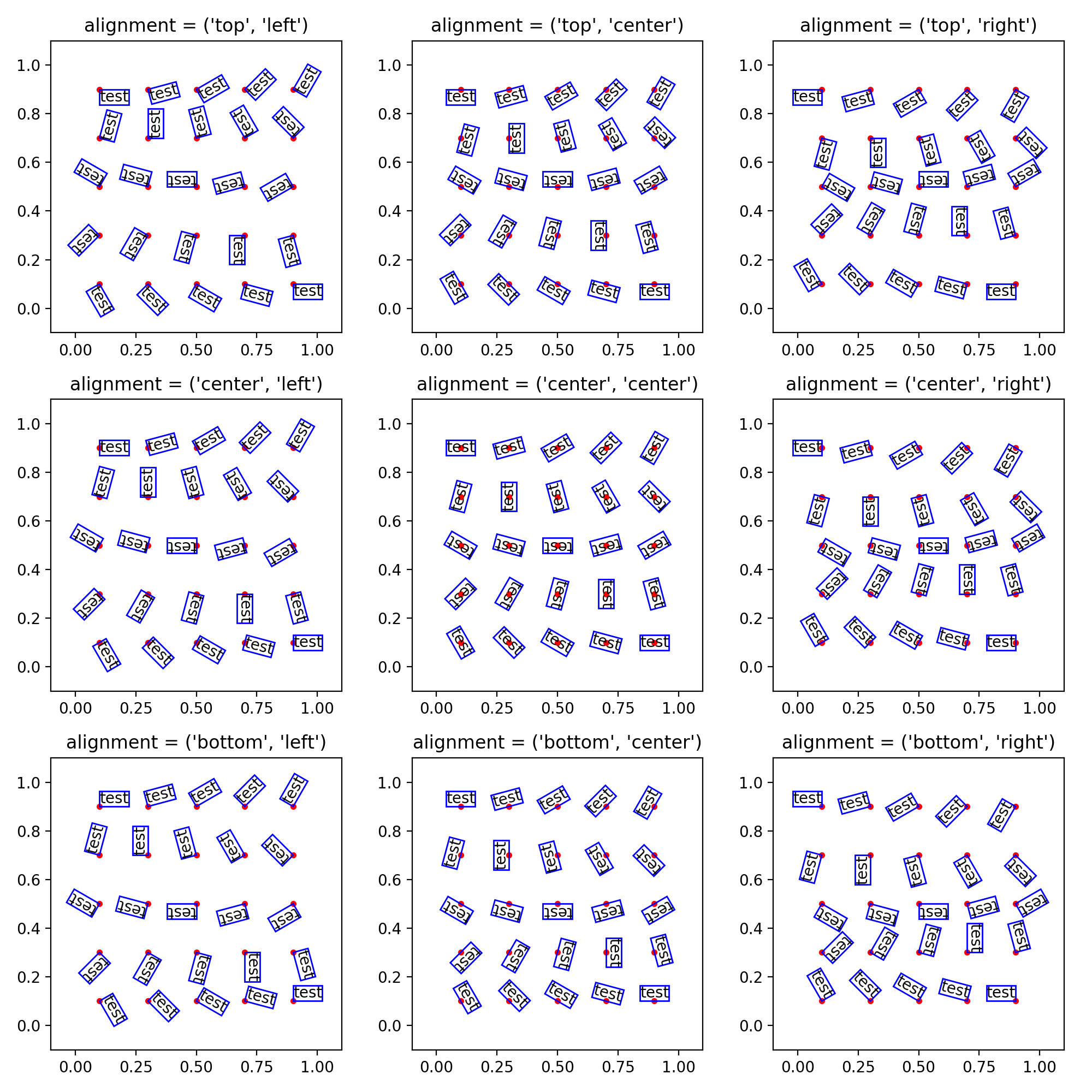 
Как соотношение сторон graph, axes, а также figure Принимая во внимание, этот подход также устойчив к изменению размера фигуры.
Я думаю, что, рассматривая методы set_ha(), set_va(), set_rotation(), а также set_position() так, как я, я мог сломать некоторые из оригинальных функций matplotlib.text.Text, но это должно быть относительно легко исправить путем перегрузки этих функций и замены нескольких self с super(),
Любые комментарии или предложения, как улучшить это, будут высоко оценены. Кроме того, если вам случится проверить это и найти какие-либо ошибки или недостатки, пожалуйста, дайте мне знать, и я постараюсь их исправить. Надеюсь, это кому-нибудь пригодится:)