Как создать случайно ориентированный круг высокой размерности в Python?

Question

Я хочу создать случайно ориентированный круг в R^n. Я был в состоянии успешно генерировать точки на поверхности n-сферы. Я читал, что вы можете пересечь его с плоскостью и получить круг, но я не знаю, как это сделать в Python.

Или есть какой-то другой способ создать его в Python?

Спасибо!

Answer 1

Поскольку вы уже знаете, как создать случайную точку на поверхности n-сферы, просто сгенерируйте две такие точки, назовите их P1 а также P2, Это определит плоскость, в которой будет лежать круг.

Я предполагаю, что обе эти точки находятся на расстоянии 1 от начала координат (что будет верно, если вы выбрали 1 в качестве радиуса вашей n-сферы). Если нет, разделите каждую точку на ее длину.

Теперь мы хотим сделать P2 перпендикулярно к P1, Это может быть сделано

P2 = P2 - dot(P1, P2) P1
P2 = P2 / || P2 ||

Затем для каждой точки вы можете сгенерировать случайный угол между 0 и 2pi. Преобразуйте этот угол в точку на окружности:

cos(angle) * P1 + sin(angle) * P2.

Answer 2

Для этого вам нужно использовать 2 базисных вектора.

1. Генерация случайной единицы ND вектора U

   так что просто создайте массив из N случайных чисел ui = <-1,+1> а затем нормализовать до размера блока, разделив их все на размер sqrt(u0^2+u1^2+...) Остерегайтесь U не должно быть ноль!!!

2. Создать ND вектор V который перпендикулярен U

   В 2D и 3D это так просто, как вы можете просто поменять местами x,y и отрицание одного в 2D или использование перекрестного произведения в 3D. К сожалению, перекрестное произведение не определено в ND (по крайней мере, насколько мне известно), поэтому вам нужно сгенерировать ненулевой вектор, для которого скалярное произведение равно нулю:

   (U.V) = dot(U,V) = 0
   u0.v0 + u1.v1 . u2.v2 + ... = 0
   

   Таким образом, вы можете создать некоторые элементы как случайные и подогнать остальные (так что сумма равна нулю). Для выравнивания вы можете использовать абс выше vi где ui Абс ниже... После этого нормализуется V к размеру блока.

   В приведенном ниже примере C++ я использовал этот подход:

   1. вычислить случайный v[i]=< -1 , +1 > такое, что произведение частичной точки любовно по величине (так что просто вычислите знак так u[i]*v[i] отрицательно к частичному точечному произведению)
   2. найти любой ненулевой u[i] и пересчитать v[i] так что точка продукта равна нулю
   3. нормализовать V к размеру блока

   Остерегайтесь также V не должно быть ноль!!!

3. Круг в НД

   используйте простое параметрическое уравнение:

   P(t) = center + radius*cos(t)*U + radius*sin(t)*V
   

   куда t = < 0 , 2*Pi >

Вот простой C++ пример генерации U,V:

//---------------------------------------------------------------------------
const int n=5; // dimension count
//---------------------------------------------------------------------------
double nd_dot(double *a,double *b)  // = (a.b)
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*b[i];
    return c;
    }
//---------------------------------------------------------------------------
void nd_unit(double *a) // a = a / |a|
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
    c=sqrt(c); if (c>1e-10) c=1.0/c; else c=0.0;
    for (i=0;i<n;i++) a[i]*=c;
    }
//---------------------------------------------------------------------------
double nd_length(double *a) // = |a|
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
    return sqrt(c);
    }
//---------------------------------------------------------------------------
void nd_rnd(double *a)  // a = (? ? ? ... ?) , |a| = 1.0
    {
    int i; double c;
    for (;;)
        {
        for (i=0;i<n;i++) a[i]=Random()-0.5;
        for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
        if (c>1e-20) break;
        }
    c=1.0/sqrt(c);
    for (i=0;i<n;i++) a[i]*=c;
    }
//---------------------------------------------------------------------------
void nd_perpendicular(double *a,double *b)  // a = (? ? ? ... ?) , |a| = 1.0 , (a.b) = 0.0
    {
    if (n==1)   // 1D case
        {
        if (fabs(b[0]>1e-10)) a[0]=1.0; else a[0]=1.0;
        return;
        }
    int i; double c1,s;
    for (c1=0.0,i=0;i<n;i++)                    // c1 = dot(a,b)
        {
        s=1.0;                                  // s = signum of a[i] so (a.b) -> 0
        if (b[i]<0.0) s=-1.0;
        if (c1*s>0.0) s=-s;
        a[i]=s*Random();
        c1+=a[i]*b[i];
        }
    for (i=0;i<n;i++)                           // correct single element so (a.b) = 0
     if (fabs(b[i])>1e-10)
        {
        c1-=a[i]*b[i];
        a[i]=-c1/b[i];
        break;
        }
    nd_unit(a);
    }
//---------------------------------------------------------------------------
AnsiString nd_prn(double *a) // this is for printing you can ignore this
    {
    int i; AnsiString s="( ";
    for (i=0;i<n;i++) s+=AnsiString().sprintf("%6.3lf ",a[i]);
    s+=" )"; return s;
    }
//---------------------------------------------------------------------------
// This is usage example in VCL you can ignore this:
__fastcall TForm1::TForm1(TComponent* Owner):TForm(Owner)
    {
    double u[n],v[n];
    Randomize();
    for (int i=0;i<10;i++)
        {
        nd_rnd(u);
        nd_perpendicular(v,u);
        mm_log->Lines->Add("U = "+nd_prn(u));
        mm_log->Lines->Add("V = "+nd_prn(v));
        mm_log->Lines->Add("(U.V) = "+AnsiString().sprintf("%6.3lf",nd_dot(u,v)));
        }
    }
//-------------------------------------------------------------------------

И результат этого для подтверждения подхода:

U = ( -0.526 -0.623 -0.535 -0.215 -0.044  )
V = (  0.620 -0.023 -0.287 -0.682 -0.260  )
(U.V) = -0.000
U = (  0.444  0.282  0.517 -0.203  0.644  )
V = (  0.072 -0.564 -0.499  0.134  0.640  )
(U.V) = -0.000
U = (  0.636  0.339  0.357 -0.022 -0.594  )
V = ( -0.559 -0.015 -0.108 -0.497 -0.655  )
(U.V) =  0.000
U = ( -0.626 -0.195  0.491 -0.374 -0.435  )
V = ( -0.722 -0.063 -0.541  0.039  0.424  )
(U.V) =  0.000
U = ( -0.532 -0.481  0.467 -0.517  0.019  )
V = (  0.536 -0.716 -0.344 -0.205 -0.199  )
(U.V) = -0.000
U = (  0.696 -0.588  0.018 -0.078  0.405  )
V = ( -0.106 -0.514 -0.645 -0.079 -0.550  )
(U.V) =  0.000
U = (  0.072  0.679  0.124 -0.204 -0.690  )
V = (  0.995 -0.058  0.041  0.060  0.037  )
(U.V) = -0.000
U = ( -0.742 -0.283  0.579 -0.150  0.109  )
V = ( -0.043 -0.798 -0.512 -0.308 -0.066  )
(U.V) = -0.000
U = (  0.606  0.389 -0.551  0.041 -0.420  )
V = ( -0.457 -0.153 -0.489 -0.691 -0.228  )
(U.V) =  0.000
U = (  0.947 -0.225  0.156 -0.075  0.151  )
V = (  0.125 -0.153 -0.043 -0.034 -0.979  )
(U.V) = -0.000

[Edit1] проблема случайности

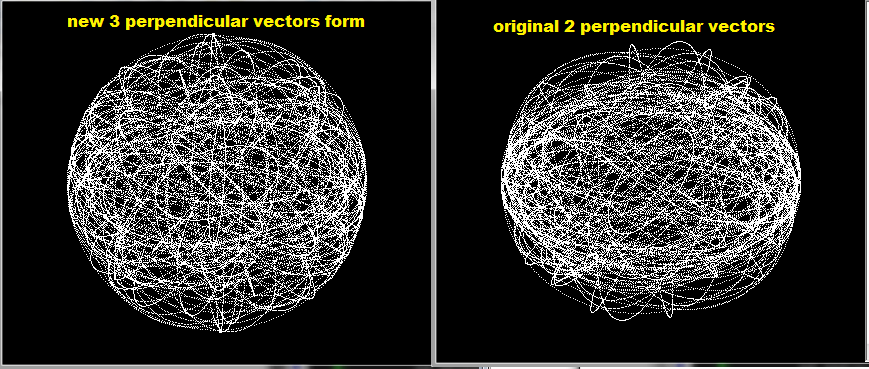
Как указал @RoobieNuby, вышеописанный метод может иметь проблемы со случайностью (у плоскостей не будет равномерного распределения). После некоторого тестирования я подтвердил это:

Итак, я проверил 3 и 2 формы базисных векторов, и разницу можно увидеть визуально. Справа приведенный выше метод в 5D (усеченный до 2D вида), а слева новая форма, полученная следующим образом:

//$$---- Form CPP ----
//---------------------------------------------------------------------------
#include <vcl.h>
#include <math.h>
#pragma hdrstop
#include "Unit1.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
Graphics::TBitmap *bmp=NULL;
int xs=0,ys=0,**pyx=NULL;

const int n=5;
//---------------------------------------------------------------------------
double nd_dot(double *a,double *b)  // = (a.b)
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*b[i];
    return c;
    }
//---------------------------------------------------------------------------
void nd_unit(double *a) // a = a / |a|
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
    c=sqrt(c); if (c>1e-10) c=1.0/c; else c=0.0;
    for (i=0;i<n;i++) a[i]*=c;
    }
//---------------------------------------------------------------------------
double nd_length(double *a) // = |a|
    {
    int i; double c;
    for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
    return sqrt(c);
    }
//---------------------------------------------------------------------------
void nd_rnd(double *a)  // a = (? ? ? ... ?) , |a| = 1.0
    {
    int i; double c;
    for (;;)
        {
        for (i=0;i<n;i++) a[i]=Random()-0.5;
        for (c=0.0,i=0;i<n;i++) c+=a[i]*a[i];
        if (c>1e-20) break;
        }
    c=1.0/sqrt(c);
    for (i=0;i<n;i++) a[i]*=c;
    }
//---------------------------------------------------------------------------
void nd_perpendicular(double *a,double *b)  // a = (? ? ? ... ?) , |a| = 1.0 , (a.b) = 0.0
    {
    if (n==1)   // 1D case
        {
        if (fabs(b[0]>1e-10)) a[0]=1.0; else a[0]=1.0;
        return;
        }
    int i; double c,s;
    for (c=0.0,i=0;i<n;i++)                     // c = dot(a,b)
        {
        s=1.0;                                  // s = signum of a[i] so (a.b) -> 0
        if (b[i]<0.0) s=-1.0;
        if (c*s>0.0) s=-s;
        a[i]=s*Random();
        c+=a[i]*b[i];
        }
    for (i=0;i<n;i++)                           // correct single element so (a.b) = 0
     if (fabs(b[i])>1e-10)
        {
        c-=a[i]*b[i];
        a[i]=-c/b[i];
        break;
        }
     nd_unit(a);
    }
//---------------------------------------------------------------------------
void nd_perpendicular(double *a,double *b,double *c) // a = (? ? ? ... ?) , |a| = 1.0 , (a.b) = 0.0 , (a.c) = 0.0
    { // this is not in-place so (&a != &b) and (&a != &c)
    int i,e; double ab,ac;
    // spec cases
    if (n<3) { for (i=0;i<n;i++) a[i]=0.0; return; }
    // init
    for (i=0;i<n;i++) a[i]=1.0;
    ab = nd_dot(a,b);
    ac = nd_dot(a,c);
    // tune until dot products near zero
    for (e=0;(e<1000)&&(fabs(ab)+fabs(ac)>=1e-5);e++)   // max 1000 iterations so it will not hang up
     for (i=0;i<n;i++)
        {
        ab-=a[i]*b[i];
        ac-=a[i]*c[i];
             if (fabs(b[i])>fabs(c[i])) a[i]=-ab/b[i];
        else if (fabs(b[i])<fabs(c[i])) a[i]=-ac/c[i];
        else if (fabs(ab)>=fabs(ac)) a[i]=-ab/b[i];
        else                         a[i]=-ac/c[i];
        ab+=a[i]*b[i];
        ac+=a[i]*c[i];
        }
    nd_unit(a);
    }
//---------------------------------------------------------------------------
AnsiString nd_prn(double *a)
    {
    int i; AnsiString s="( ";
    for (i=0;i<n;i++) s+=AnsiString().sprintf("%6.3lf ",a[i]);
    s+=" )"; return s;
    }
//---------------------------------------------------------------------------
// VCL application init (can ignore this)
__fastcall TForm1::TForm1(TComponent* Owner):TForm(Owner)
    {
    bmp=new Graphics::TBitmap;
    bmp->HandleType=bmDIB;
    bmp->PixelFormat=pf32bit;
    if (bmp==NULL) Application->Terminate();
    }
//-------------------------------------------------------------------------
// VCL application resize event (can ignore this)
void __fastcall TForm1::FormResize(TObject *Sender)
    {
    if (bmp==NULL) return;
    xs=ClientWidth-mm_log->Width;
    ys=ClientHeight;
    bmp->SetSize(xs,ys);
    xs=bmp->Width;
    ys=bmp->Height;
    if (pyx) delete[] pyx;
    pyx=new int*[ys];
    for (int y=0;y<ys;y++) pyx[y]=(int*)bmp->ScanLine[y];
    Paint();
    }
//---------------------------------------------------------------------------
// VCL application exit (can ignore this)
void __fastcall TForm1::FormDestroy(TObject *Sender)
    {
    if (bmp) delete   bmp; bmp=NULL;
    if (pyx) delete[] pyx; pyx=NULL;
    }
//---------------------------------------------------------------------------
// VCL application repaint (consider this void main()...)
void __fastcall TForm1::FormPaint(TObject *Sender)
    {
    if (bmp==NULL) return;
    if (pyx==NULL) return;
    int i,e,x,y;
    double u[n],v[n],w[n];
    double a,da,x0,y0,r,c,s;
    Randomize();

    // clear screen (xs,ys is resolution, pyx is direct pixel access to bitmap bmp)
    for (y=0;y<ys;y++)
     for (x=0;x<xs;x++)
      pyx[y][x]=0x00000000;

    da=1.0*M_PI/180.0;              // angle step
    x0=0.5*xs;                      // center
    y0=0.5*ys;
    r=150.0;                        // radius
    // 100 random circles
    for (i=0;i<100;i++)
        {
        // 3 vector form
        nd_rnd(w);                  // W random unit vector (normal of the plane)
        nd_perpendicular(v,w);      // V perpendicular to W
        nd_perpendicular(u,v,w);    // U perpendicular to V and W
        // old 2 vector form
//      nd_rnd(u);
//      nd_perpendicular(v,u);

        for (e=1,a=0.0;e;a+=da)     // circle points loop
            {
            if (a>=2.0*M_PI) { e=0; a=0.0; }
            c=r*cos(a);
            s=r*sin(a);
            x=double(x0+(c*u[0])+(s*v[0]));     // use just x,y for render
            y=double(y0+(c*u[1])+(s*v[1]));
            if ((x>=0)&&(x<xs)&&(y>=0)&&(y<ys)) // if inside screen
             pyx[y][x]=0x00FFFFFF;              // render it
            }
        // debug info log to see the U,V,W as numbers
        if (i==0)
            {
            mm_log->Text="";
            mm_log->Lines->Add("U = "+nd_prn(u));
            mm_log->Lines->Add("V = "+nd_prn(v));
            mm_log->Lines->Add("W = "+nd_prn(w));
            mm_log->Lines->Add("(U.V) = "+AnsiString().sprintf("%6.3lf",nd_dot(u,v)));
            mm_log->Lines->Add("(U.W) = "+AnsiString().sprintf("%6.3lf",nd_dot(u,w)));
            mm_log->Lines->Add("(W.V) = "+AnsiString().sprintf("%6.3lf",nd_dot(w,v)));
            }
        }
    // refresh Application window with bitmap (bacbuffering)
    Canvas->Draw(0,0,bmp);
    }
//---------------------------------------------------------------------------
// VCLo mouse wheel event ... just force repaint on mouse wheel to check the randomness in time (can ignore this)
void __fastcall TForm1::FormMouseWheel(TObject *Sender, TShiftState Shift, int WheelDelta, TPoint &MousePos, bool &Handled)
    {
    Paint();
    }
//---------------------------------------------------------------------------

Важные вещи здесь void nd_perpendicular(double *a,double *b,double *c); функция, которая возвращает перпендикулярный вектор обоим b,c, Чтобы сделать это надежным (если случайность имеет значение) в ND, вы должны иметь n векторы не только 3,

Работа функции аналогична предыдущей. Разница только в том, что мы оптимизируем более одного точечного продукта одновременно. Таким образом, вам нужно выбрать, какое точечное произведение оптимизировать для каждой оси (на основе значения координаты абс перпендикулярного вектора). Таким образом, вы должны переписать это, чтобы оптимизировать n-1 Точка продуктов сразу.

1. Создайте 1st вектор (нормальный)
2. Создайте 2nd вектор (1 точечный продукт для оптимизации)
3. Создайте 3th вектор (2 точечные продукты для оптимизации)
4. Создайте 4th вектор (3 точечные продукты для оптимизации)
5. ...
6. Создайте n-th вектор (n-1 точечные продукты для оптимизации)
7. использовать любой 2 (кроме первого) векторы в качестве основы (их можно выбрать случайным образом)
8. создай свой круг

Похоже просто 3 векторов достаточно для n>=3 (так что вы можете игнорировать № 4, № 5), но чтобы подтвердить, что наверняка понадобится какой-то статистический анализ, который мне лень делать.

[Edit2] вектор, перпендикулярный большему числу векторов...

Реализовали перпендикулярное векторное вычисление точечного произведения из другого ответа. И вычисление перпендикулярного вектора для нескольких векторов:

//---------------------------------------------------------------------------
void nd_perpendicular(double *a,double *b)  // a = (? ? ? ... ?) , |a| = 1.0 , (a.b) = 0.0
    {
    int i; double tmp[n],dot,len;
    // |dot| limit to consider as non parallel
    len=0.7*nd_length(b);
    // tmp = random unit vector not parallel to b
    for (;;)
        {
        nd_rnd(tmp);
        dot=nd_dot(b,tmp);
        if (fabs(dot)<=len) break;
        }
    // make a unit and perpendicular to b
    for (i=0;i<n;i++) a[i]=tmp[i]-(dot*b[i]);
    nd_unit(a);
    }
//---------------------------------------------------------------------------
void nd_perpendicular(double *a,double *v0,double *v1,double *v2=NULL,double *v3=NULL,double *v4=NULL,double *v5=NULL,double *v6=NULL,double *v7=NULL,double *v8=NULL,double *v9=NULL)
    {
    // this is not in-place so (&a != &b) and (&a != &c)
    // a = unit vector perpendicular to all not NULL vectors v0,v1,v2,v3,...
    const int M=10; // vi operands max count
    int i,j,k,e,m; double dot[M],*v[M]={v0,v1,v2,v3,v4,v5,v6,v7,v8,v9},q;
    // spec cases
    if (n<3) { for (i=0;i<n;i++) a[i]=0.0; return; }
    // init
    for (i=0;i<n;i++) a[i]=1.0;
    nd_rnd(a);
    for (m=0,j=0;j<M;j++) if (v[j]) { m=j+1; dot[j]=nd_dot(a,v[j]); } else dot[j]=0.0;
    // tune until dot products near zero
    for (e=0;e<1000;e++)    // max 1000 iterations so it will not hang up
        {
        for (q=0.0,j=0;j<m;j++) q+=fabs(dot[j]);
        if (q<1e-3) { e=-1; break; }
        // k = index of abs max dot
        for (k=0,j=0;j<m;j++) if (fabs(dot[j])>=fabs(dot[k])) k=j;
        // i = index of abs max coordinate of v[k]
        for (i=0,j=0;j<n;j++) if (fabs(v[k][j])>=fabs(v[k][i])) i=j;
        // update dots and a[i]
        for (j=0;j<m;j++) dot[j]-=a[i]*v[j][i];
        a[i]=-dot[k]/v[k][i];
        for (j=0;j<m;j++) dot[j]+=a[i]*v[j][i];
        }

    if (e>=0)
     for (e=0;e<1000;e++)   // max 1000 iterations so it will not hang up
        {
        for (q=0.0,j=0;j<m;j++) q+=fabs(dot[j]);
        if (q<1e-3) { e=-1; break; }
        for (i=0;i<n;i++)
            {
            // k = index of abs max vec
            for (k=0,j=0;j<m;j++) if (fabs(v[j][i])>=fabs(v[k][i])) k=j;
            // update dots and a[i]
            for (j=0;j<m;j++) dot[j]-=a[i]*v[j][i];
            a[i]=-dot[k]/v[k][i];
            for (j=0;j<m;j++) dot[j]+=a[i]*v[j][i];
            }
        }
    nd_unit(a);
    }
//---------------------------------------------------------------------------

Слишком высокая надежность. Используется 2 разных итерационных подхода. Вот пример использования (n=5):

// nd_perpendicular test
double V[n][n]; int x,y;
nd_rnd(V[0]);
nd_perpendicular(V[1],V[0]);
nd_perpendicular(V[2],V[1],V[0]);
nd_perpendicular(V[3],V[2],V[1],V[0]);
nd_perpendicular(V[4],V[3],V[2],V[1],V[0]);
for (x=0;x<n;x++)
 for (y=x+1;y<n;y++)
  mm_log->Lines->Add(AnsiString().sprintf("(V%i.V%i) = %6.3lf",x,y,nd_dot(V[x],V[y])));

Answer 3

Далее предполагается, что под многомерным кругом вы подразумеваете пересечение N- сферы с N- гиперплоскостью, содержащей центр сферы (т.е. N-1-сферу в N+ 1-пространстве).

Вы можете сделать следующее (если вы находитесь в N + 1-пространстве, учитывая N- сферу):

• выберите нормальный вектор n, ваш круг будет подмножеством сферы, ортогональной n
• используйте SVD, чтобы получить ортонормированный базис B для ортогонального дополненияn
• используйте свой метод, чтобы создать точки p на сфере N-1 и умножить их на B (B равно N+1 x N, поэтому Bp будет в N+ 1-пространстве)

Answer 4

В качестве полной реализации Python:

N=3 # dimensions
R=1 # radius
npoints=1000
from numpy.random import rand
from numpy.linalg import norm
from numpy import dot,sin,cos,outer,pi
V1,V2,origin=rand(3,N)
u1=V1/norm(V1)
u2=V2/norm(V2)
V3=u1-dot(u1,u2)*u2
u3=V3/norm(V3)
print(norm(u2),norm(u3),dot(u2,u3))
#1.0 1.0 0.0
#u2,u3 is orthonormed 
theta=np.arange(0,2*pi,2*pi/npoints)

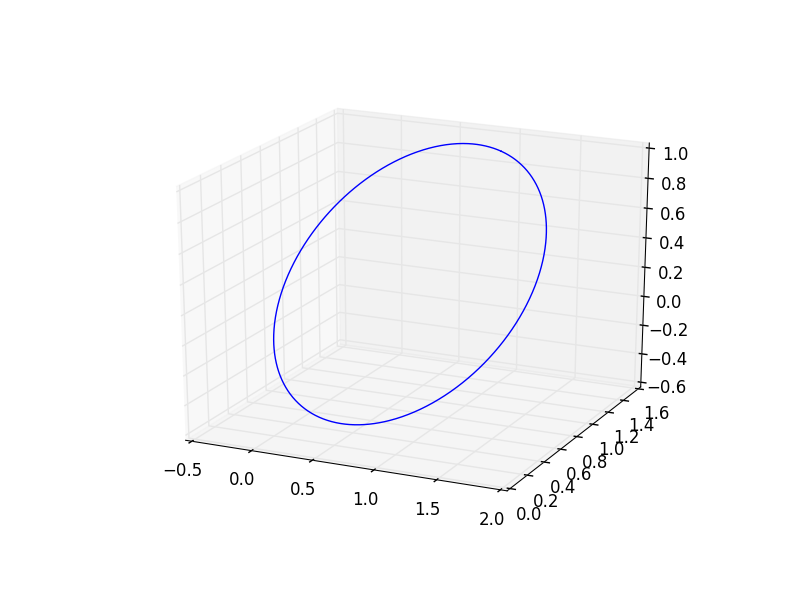
circle=origin+R*(outer(cos(theta),u2)+outer(sin(theta),u3))

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(*circle.T)
plt.show()