Объединенная область перекрывающихся кругов
Недавно я столкнулся с проблемой, когда у меня было четыре круга (средние точки и радиус), и мне нужно было вычислить площадь объединения этих кругов.
Пример изображения:

Для двух кругов это довольно просто,
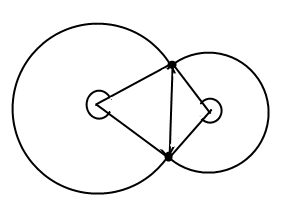
Я могу просто вычислить долю площади каждого круга, которая не находится внутри треугольников, а затем вычислить площадь треугольников.
Но есть ли умный алгоритм, который я могу использовать, когда больше двух кругов?
15 ответов
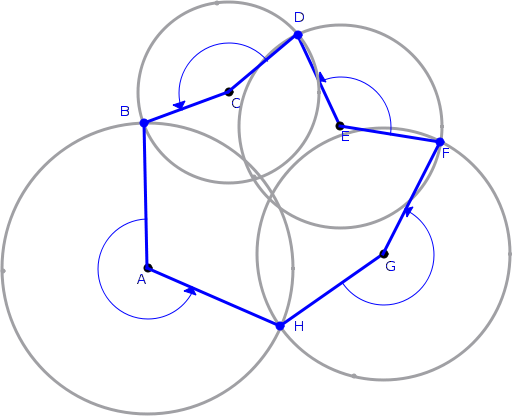
Найдите все пересечения окружностей по внешнему периметру (например, B,D,F,H на следующей диаграмме). Соедините их вместе с центрами соответствующих кругов, чтобы сформировать многоугольник. Площадь объединения окружностей - это площадь многоугольника + площадь срезов окружности, определяемая последовательными точками пересечения и центром окружности между ними. Вам также необходимо учитывать любые дыры.
Я уверен, что есть умный алгоритм, но вот глупый, чтобы избавиться от необходимости искать его;
- поместите ограничивающую рамку вокруг кругов;
- генерировать случайные точки в пределах ограничительной рамки;
- выяснить, находится ли случайная точка внутри одного из кругов;
- вычислить площадь с помощью простого сложения и деления (пропорции_по_пунктам_области_области_пределения_объектов).
Конечно, это глупо, но:
- вы можете получить максимально точный ответ, просто набрав больше очков;
- он будет работать для любых форм, для которых вы можете рассчитать разницу между внутренним и внешним;
- он будет красиво распараллеливаться, чтобы вы могли использовать все свои ядра.
Ответ Антса Аасмы дал основную идею, но я хотел сделать ее немного более конкретной. Посмотрите на пять кружков ниже и то, как они были разложены.
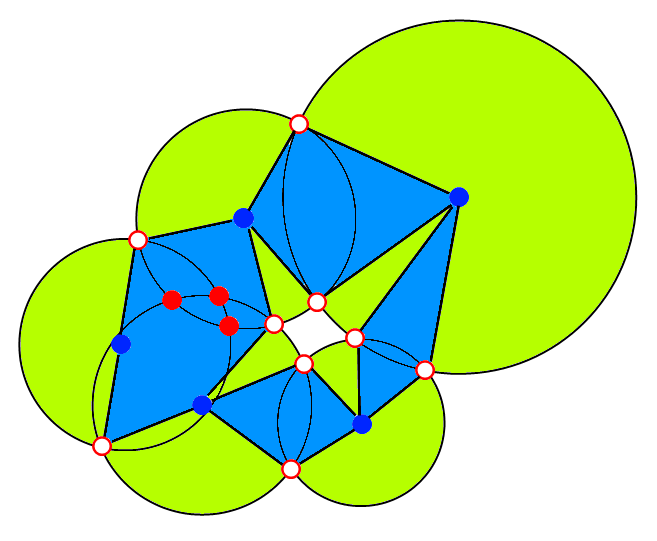
- Синие точки - это центры кругов.
- Красные точки - это пересечения границ окружности.
- Красные точки с белым внутренним пространством - это пересечения границ окружностей, которые не содержатся ни в каких других кругах.
Определить эти 3 типа точек легко. Теперь создайте структуру данных графа, где узлами являются синие точки и красные точки с белым интерьером. Для каждого круга поместите ребро между серединой круга (синяя точка) и каждым из его пересечений (красные точки с белым внутренним пространством) на его границе.
Это разбивает круговое объединение на набор многоугольников (заштрихованный синий) и круговых круговых кусочков (заштрихованный зеленый), которые попарно не пересекаются и покрывают исходный союз (то есть разделение). Так как каждая часть здесь является чем-то, что легко вычислить по площади, вы можете вычислить площадь объединения, суммируя области фигур.
Для решения, отличного от предыдущего, вы можете получить оценку с произвольной точностью, используя квадродерево.
Это также работает для любого объединения фигур, если вы можете определить, находится ли квадрат внутри или снаружи или пересекает форму.
Каждая ячейка имеет одно из состояний: пустое, полное, частичное
Алгоритм состоит в "рисовании" кругов в дереве квадрантов, начиная с низкого разрешения (например, 4 ячейки помечены как пустые). Каждая ячейка является либо:
- внутри хотя бы одного круга, затем отметьте ячейку как заполненную,
- за пределами всех кругов отметьте ячейку как пустую,
- иначе пометьте ячейку как частичную.
Когда это сделано, вы можете вычислить оценку площади: полные ячейки дают нижнюю границу, пустые ячейки дают верхнюю границу, частичные ячейки дают ошибку максимальной площади.
Если ошибка слишком велика для вас, вы уточняете частичные ячейки, пока не получите правильную точность.
Я думаю, что это будет легче реализовать, чем геометрический метод, который может потребовать обработки множества особых случаев.
Мне нравится подход к случаю 2 пересекающихся кругов - вот как я бы использовал небольшое изменение этого же подхода для более сложного примера.
Это может дать лучшее понимание обобщения алгоритма для большего числа полуперекрывающихся кругов.
Разница здесь в том, что я начинаю со связывания центров (так что есть вершина между центрами окружностей, а не между местами, где пересекаются окружности). Я думаю, что это позволяет лучше обобщать.
(на практике, может быть, стоит метод Монте-Карло)
Если вам нужен дискретный (в отличие от непрерывного) ответ, вы можете сделать что-то похожее на алгоритм рисования пикселей.
Нарисуйте круги на сетке, а затем раскрасьте каждую ячейку сетки, если она в основном содержится внутри круга (то есть, по крайней мере, 50% ее площади находится внутри одного из кругов). Сделайте это для всей сетки (где сетка охватывает всю область, покрытую кругами), затем посчитайте количество цветных ячеек в сетке.
Подход к рисованию пикселей (как предложено @Loadmaster) превосходит математическое решение во многих отношениях:
- Реализация намного проще. Вышеупомянутая проблема может быть решена менее чем в 100 строках кода, как демонстрирует это решение JSFiddle (в основном потому, что оно концептуально намного проще и не имеет краевых случаев или исключений, с которыми нужно иметь дело).
- Он легко адаптируется к более общим проблемам. Он работает с любой формой, независимо от морфологии, до тех пор, пока ее можно рендерить с помощью библиотек двумерного рисования (т. Е. "Всех!") - кругов, эллипсов, сплайнов, многоугольников, назовите это. Черт, даже растровые изображения.
- Сложность решения для рисования пикселей составляет ~O[n], по сравнению с ~O[n*n] для математического решения. Это означает, что он будет работать лучше по мере увеличения числа фигур.
- И если говорить о производительности, вы часто будете получать аппаратное ускорение бесплатно, так как большинство современных 2D-библиотек (как я полагаю, на холсте HTML5) перекладывают рендеринг на графические ускорители.
Единственным недостатком пиксельной живописи является конечная точность решения. Но это настраивается путем простого рендеринга на большие или меньшие холсты в зависимости от ситуации. Также обратите внимание, что сглаживание в коде 2D-рендеринга (часто включаемое по умолчанию) даст точность выше уровня пикселей. Так, например, рендеринг фигуры 100x100 в холст с такими же размерами должен, я думаю, дать точность порядка 1 / (100 x 100 x 255) = .000039% ... что, вероятно, "достаточно хорошо" для всех, кроме самых сложных проблем.
<p>Area computation of arbitrary figures as done thru pixel-painting, in which a complex shape is drawn into an HTML5 canvas and the area determined by comparing the number of white pixels found in the resulting bitmap. See javascript source for details.</p>
<canvas id="canvas" width="80" height="100"></canvas>
<p>Area = <span id="result"></span></p>
// Get HTML canvas element (and context) to draw into
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
// Lil' circle drawing utility
function circle(x,y,r) {
ctx.beginPath();
ctx.arc(x, y, r, 0, Math.PI*2);
ctx.fill();
}
// Clear canvas (to black)
ctx.fillStyle = 'black';
ctx.fillRect(0, 0, canvas.width, canvas.height);
// Fill shape (in white)
ctx.fillStyle = 'white';
circle(40, 50, 40);
circle(40, 10, 10);
circle(25, 15, 12);
circle(35, 90, 10);
// Get bitmap data
var id = ctx.getImageData(0, 0, canvas.width, canvas.height);
var pixels = id.data; // Flat array of RGBA bytes
// Determine area by counting the white pixels
for (var i = 0, area = 0; i < pixels.length; i += 4) {
area += pixels[i]; // Red channel (same as green and blue channels)
}
// Normalize by the max white value of 255
area /= 255;
// Output result
document.getElementById('result').innerHTML = area.toFixed(2);
Существуют эффективные решения этой проблемы с использованием так называемых диаграмм мощности. Это действительно тяжелая математика, а не то, что я бы хотел взяться за дело. Для "легкого" решения ищите алгоритмы линейной развертки. Основной принцип здесь заключается в том, что вы делите фигуру на полосы, где вычисление площади в каждой полосе относительно просто.
Таким образом, на рисунке, содержащем все круги, где ничего не стирается, нарисуйте горизонтальную линию в каждой позиции, которая является либо вершиной круга, либо нижней частью круга, либо пересечением двух кругов. Обратите внимание, что внутри этих полос все области, которые вам нужно рассчитать, выглядят одинаково: "трапеция" с двумя сторонами, замененными круглыми сегментами. Поэтому, если вы можете решить, как рассчитать такую форму, вы просто делаете это для всех отдельных фигур и складываете их вместе. Сложность этого наивного подхода составляет O(N^3), где N - количество кружков на рисунке. С помощью некоторого умного использования структуры данных вы могли бы улучшить этот метод развертки строки до O(N^2 * log(N)), но если вам это действительно не нужно, это, вероятно, не стоит проблем.
Хм, очень интересная проблема. Мой подход, вероятно, будет что-то вроде следующего:
- Разработайте способ определения областей пересечения между произвольным числом кругов, то есть, если у меня есть 3 круга, мне нужно уметь определить, что такое пересечение между этими кругами. Метод "Монте-Карло" был бы хорошим способом приблизиться к этому ( http://local.wasp.uwa.edu.au/~pbourke/geometry/circlearea/).
- Исключить любые круги, которые целиком содержатся в другом большем круге (посмотрите на радиус и модуль расстояния между центром двух кругов), я не думаю, что это обязательно.
- Выберите 2 круга (назовите их A и B) и определите общую площадь, используя эту формулу:
(это верно для любой формы, будь то круг или иное)
area(A∪B) = area(A) + area(B) - area(A∩B)
куда A ∪ B означает союз B и A ∩ B означает пересечение B (вы можете решить это с первого шага.
- Теперь продолжайте добавлять круги и продолжайте работать над областью, добавленной как сумма / вычитание областей кругов и областей пересечений между кругами. Например, для 3 кругов (назовите дополнительный круг C) мы определяем площадь по следующей формуле:
(Это то же самое, что и выше, где A был заменен на A∪B)
area((A∪B)∪C) = area(A∪B) + area(C) - area((A∪B)∩C)
куда area(A∪B) мы только что разработали, и area((A∪B)∩C) может быть найден:
area((A∪B)nC) = area((A∩C)∪(B∩C)) = area(A∩C) + area(A∩B) - area((A∩C)∩(B∩C)) = area(A∩C) + area(A∩B) - area(A∩B∩C)
Где снова вы можете найти область (A∩B∩C) сверху.
Сложный шаг - последний шаг - чем больше кругов добавляется, тем сложнее становится. Я полагаю, что есть расширение для обработки области пересечения с конечным объединением, или, в качестве альтернативы, вы сможете рекурсивно решить это.
Также, что касается использования метода Монте-Карло для аппроксимации площади итерсекции, я считаю возможным уменьшить пересечение произвольного числа окружностей до пересечения 4 из этих окружностей, которые можно точно рассчитать (не знаю, как это сделать тем не мение).
Вероятно, есть лучший способ сделать это, кстати - сложность значительно увеличивается (возможно, в геометрической прогрессии, но я не уверен) для каждого добавленного дополнительного круга.
Я работал над проблемой моделирования перекрывающихся звездных полей, пытаясь оценить истинное количество звезд по фактическим областям диска в плотных полях, где более крупные яркие звезды могут маскировать более слабые. Я тоже надеялся, что смогу сделать это с помощью строгого формального анализа, но не смог найти алгоритм для этой задачи. Я решил это, создав звездные поля на синем фоне в виде зеленых дисков, диаметр которых был определен вероятностным алгоритмом. Простая процедура может спарить их, чтобы увидеть, есть ли совпадение (превращение звездной пары в желтый); затем количество пикселей цветов генерирует наблюдаемую область для сравнения с теоретической областью. Затем генерируется кривая вероятности для истинных отсчетов. Грубая сила может быть, но, похоже, работает хорошо.
http://www.2from.com/images/simulated_star_field.gif
Вот алгоритм, который должен быть легко реализован на практике и может быть отрегулирован для получения сколь угодно маленькой ошибки:
- Приблизить каждый круг по правильному многоугольнику с центром в той же точке
- Вычислить многоугольник, который является объединением приближенных окружностей
- Рассчитать площадь слитого многоугольника
Шаги 2 и 3 могут быть выполнены с использованием стандартных, простых в поиске алгоритмов из вычислительной геометрии.
Очевидно, что чем больше сторон вы используете для каждого аппроксимирующего многоугольника, тем точнее будет ваш ответ. Вы можете приблизиться, используя вписанные и ограниченные многоугольники, чтобы получить границы для точного ответа.
Это может быть решено с помощью теоремы Грина со сложностью n^2log(n). Если вы не знакомы с теоремой Грина и хотите узнать больше, вот видео и заметки из Академии Хана. Но ради нашей проблемы, думаю, моего описания будет достаточно.
Извините за ссылки на фотографии, так как я не могу публиковать изображения.(Недостаточно очков репутации)
Если я поставлю L и M так, что
тогда RHS - это просто область Региона R, и ее можно получить, решив замкнутый интеграл или LHS, и это именно то, что мы собираемся сделать.
Все союзы можно разбить на такие непересекающиеся множества окружностей, которые пересекаются
Таким образом, интеграция вдоль пути в направлении против часовой стрелки дает нам площадь региона, а интеграция по часовой стрелке дает нам отрицательный угол области. Так
AreaOfUnion = (Интеграция вдоль красных дуг в направлении против часовой стрелки + Интеграция вдоль синих дуг в направлении по часовой стрелке)
Но классный трюк в том, что для каждого круга, если мы интегрируем дуги, которые не находятся внутри какого-либо другого круга, мы получаем требуемую площадь, т.е. получаем интеграцию в направлении против часовой стрелки вдоль всех красных дуг и интеграцию вдоль всех синих дуг в направлении по часовой стрелке. РАБОТА ВЫПОЛНЕНА!!!
Даже случаи, когда круг не пересекается ни с каким другим, рассматриваются.
Вот ссылка GitHub на мой код C++
Я нашел эту ссылку, которая может быть полезной. Там, кажется, нет однозначного ответа, хотя. Гугл отвечает. Еще одна ссылка для трех кругов - теорема Харуки. Там тоже есть бумага.
У меня есть способ получить приблизительный ответ, если вы знаете, что все ваши круги будут находиться в определенной области , т.е. каждая точка в круге находится внутри прямоугольника, размеры которого вам известны. Это предположение будет справедливым, например, если все круги находятся на изображении известного размера. Если вы можете сделать это предположение, разделите область, содержащую ваше изображение, на «пиксели». Для каждого пикселя вычислите, находится ли он внутри хотя бы одного из кругов. Если это так, увеличьте промежуточную сумму на единицу. Когда вы закончите, вы знаете, сколько пикселей находится внутри хотя бы одного круга, а также знаете площадь каждого пикселя, поэтому вы можете рассчитать общую площадь всех перекрывающихся кругов.
Увеличивая «разрешение» вашего региона (количество пикселей), вы можете улучшить свое приближение.
Кроме того, если размер области, содержащей ваши круги, ограничен, и вы сохраняете разрешение (количество пикселей) постоянным, алгоритм выполняется за время O(n) (n - количество кругов). Это связано с тем, что для каждого пикселя вы должны проверить, находится ли он внутри каждого из ваших n кругов, а общее количество пикселей ограничено.
В зависимости от того, какую проблему вы пытаетесь решить, может быть достаточно получить верхнюю и нижнюю границу. Верхняя граница проста, просто сумма всех кругов. Для нижней границы вы можете выбрать один радиус, чтобы ни один из кругов не перекрывался. Чтобы лучше было найти самый большой радиус (вплоть до фактического радиуса) для каждого круга, чтобы он не перекрывался. Также должно быть довольно тривиально удалить любые полностью перекрывающиеся круги (все такие круги удовлетворяют |P_a - P_b| <= r_a), где P_a - центр круга A, P_b - центр круга B, а r_a - радиус A) и это улучшает как верхнюю, так и нижнюю границу. Вы также можете получить лучшую верхнюю границу, если будете использовать формулу пары для произвольных пар вместо просто суммы всех окружностей. Там может быть хороший способ выбрать "лучшие" пары (пары, которые приводят к минимальной общей площади.
Учитывая верхнюю и нижнюю границу, вы могли бы лучше настроить подход Монте-Карло, но ничего конкретного не приходит на ум. Другой вариант (опять же в зависимости от вашего приложения) - растеризация кругов и подсчет пикселей. Это в основном подход Монте-Карло с фиксированным распределением.