Оптимально выбрать один элемент из каждого списка
Я наткнулся на старую проблему, которая вам, вероятно, понравится вам, Mathematica/Stackru, и кажется, что она полезна для Stackru для потомков.
Предположим, у вас есть список списков, и вы хотите выбрать один элемент из каждого и поместить их в новый список, чтобы число элементов, идентичных их следующему соседу, было максимальным. Другими словами, для результирующего списка l минимизируйте Length@Split[l]. Другими словами, нам нужен список с наименьшим количеством прерываний из идентичных смежных элементов.
Например:
pick[{ {1,2,3}, {2,3}, {1}, {1,3,4}, {4,1} }]
--> { 2, 2, 1, 1, 1 }
(Или {3,3,1,1,1} одинаково хорош.)
Вот нелепое решение грубой силы:
pick[x_] := argMax[-Length@Split[#]&, Tuples[x]]
где argMax, как описано здесь:
posmax: как и argmax, но дает положение (я) элемента x, для которого f[x] является максимальным
Можете ли вы придумать что-нибудь лучше? Легендарный Карл Уолл прибил это для меня, и я раскрою его решение через неделю.
8 ответов
Я брошу это на ринг. Я не уверен, что он всегда дает оптимальное решение, но он работает по той же логике, что и некоторые другие ответы, и это быстро.
f@{} := (Sow[m]; m = {i, 1})
f@x_ := m = {x, m[[2]] + 1}
findruns[lst_] :=
Reap[m = {{}, 0}; f[m[[1]] ⋂ i] ~Do~ {i, lst}; Sow@m][[2, 1, 2 ;;]]
findruns дает закодированный вывод длины пробега, включая параллельные ответы. Если требуется вывод, как строго указано, используйте:
Flatten[First[#]~ConstantArray~#2 & @@@ #] &
Вот вариант с использованием Fold. Это быстрее на некоторых заданных фигурах, но немного медленнее на других.
f2[{}, m_, i_] := (Sow[m]; {i, 1})
f2[x_, m_, _] := {x, m[[2]] + 1}
findruns2[lst_] :=
Reap[Sow@Fold[f2[#[[1]] ⋂ #2, ##] &, {{}, 0}, lst]][[2, 1, 2 ;;]]
Не ответ, а сравнение предложенных здесь методов. Я сгенерировал наборы тестов с переменным числом подмножеств, это число варьируется от 5 до 100. Каждый набор тестов был создан с этим кодом
Table[RandomSample[Range[10], RandomInteger[{1, 7}]], {rl}]
с RL количество вовлеченных подмножеств.
Для каждого набора тестов, сгенерированного таким образом, все алгоритмы делали свое дело. Я делал это 10 раз (с тем же набором тестов) с алгоритмами, работающими в случайном порядке, чтобы выровнять эффекты порядка и эффекты случайных фоновых процессов на моем ноутбуке. Это приводит к среднему времени для данного набора данных. Вышеупомянутая линия использовалась 20 раз для каждой длины rl, из которой были рассчитаны среднее (среднее) и стандартное отклонение.
Результаты приведены ниже (по горизонтали количество подмножеств и по вертикали среднее значение AbsoluteTiming):
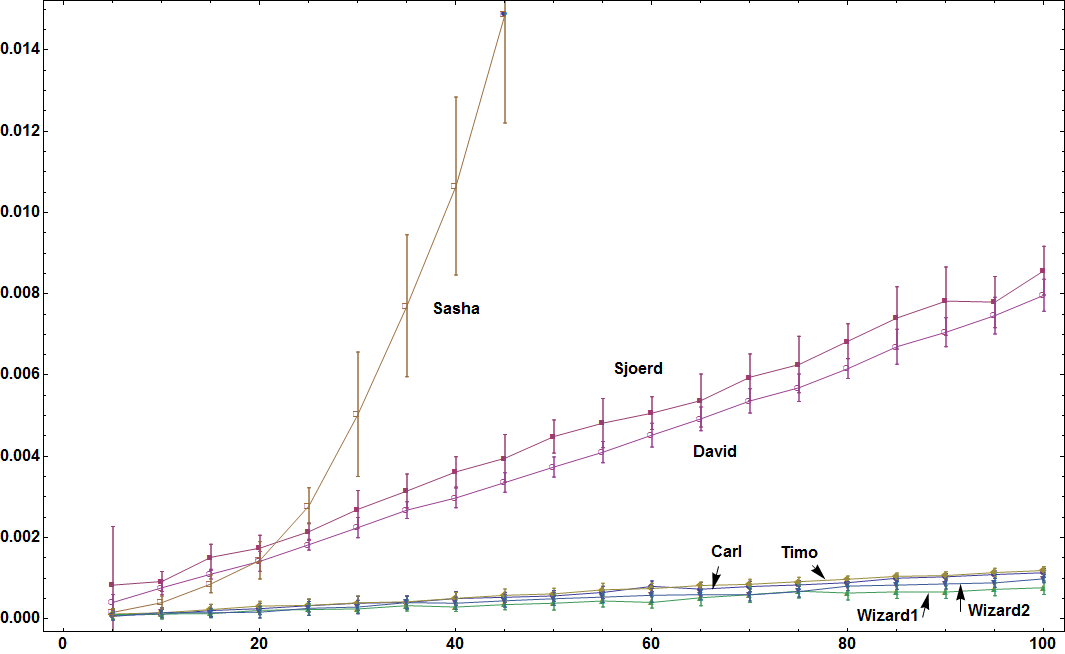
Кажется, что Mr.Wizard является (не очень ясно) победителем. Congrats!
Обновить
В соответствии с запросом Тимо здесь время определяется как функция от числа отдельных элементов подмножества, из которых можно выбрать, а также от максимального количества элементов в каждом подмножестве. Наборы данных генерируются для фиксированного количества подмножеств (50) в соответствии с этой строкой кода:
lst = Table[RandomSample[Range[ch], RandomInteger[{1, ch}]], {50}];
Я также увеличил количество наборов данных, которые я пробовал для каждого значения, с 20 до 40.
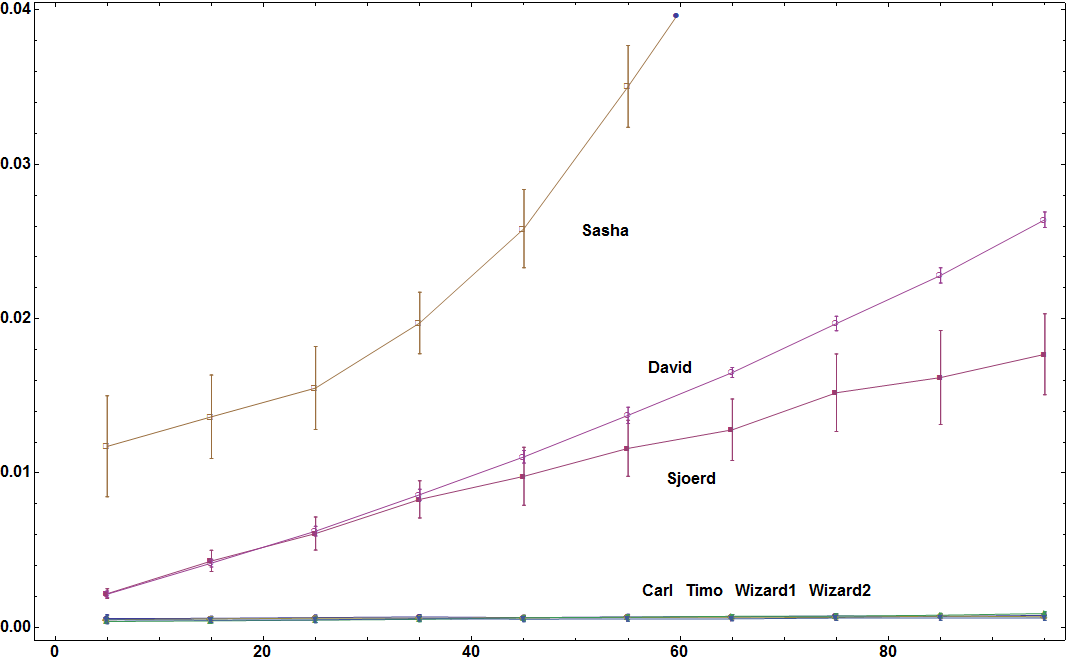
Здесь для 5 подмножеств:
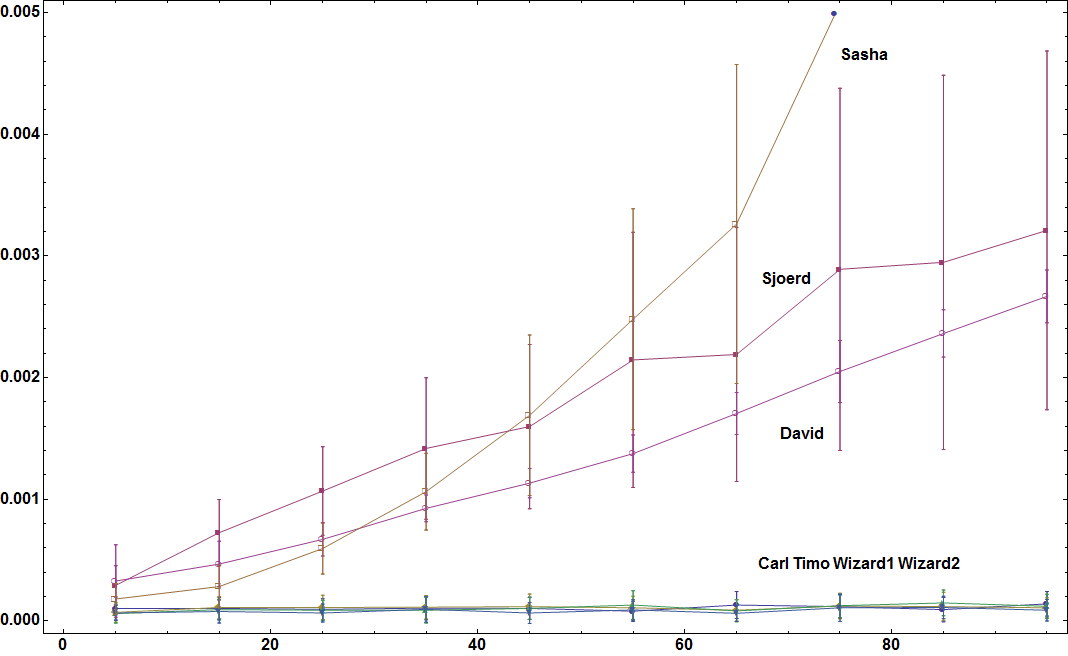
Мое решение основано на наблюдении, что "жадность хороша" здесь. Если у меня есть выбор между прерыванием цепочки и началом новой, потенциально длинной цепочки, выбор новой для продолжения не приносит мне никакой пользы. Новая цепь становится длиннее с той же суммой, что и старая цепь короче.
Итак, что алгоритм в основном делает, так это начинает с первого подсписка и для каждого из его членов находит количество дополнительных подсписков, имеющих одинаковый член, и выбирает член подсписка, который имеет большинство соседних близнецов. Затем этот процесс продолжается в подсписке в конце этой первой цепочки и так далее.
Объединяя это в рекурсивный алгоритм, мы получаем:
pickPath[lst_] :=
Module[{lengthChoices, bestElement},
lengthChoices =
LengthWhile[lst, Function[{lstMember}, MemberQ[lstMember, #]]] & /@First[lst];
bestElement = Ordering[lengthChoices][[-1]];
If[ Length[lst] == lengthChoices[[bestElement]],
ConstantArray[lst[[1, bestElement]], lengthChoices[[bestElement]]],
{
ConstantArray[lst[[1, bestElement]], lengthChoices[[bestElement]]],
pickPath[lst[[lengthChoices[[bestElement]] + 1 ;; -1]]]
}
]
]
Тестовое задание
In[12]:= lst =
Table[RandomSample[Range[10], RandomInteger[{1, 7}]], {8}]
Out[12]= {{3, 10, 6}, {8, 2, 10, 5, 9, 3, 6}, {3, 7, 10, 2, 8, 5,
9}, {6, 9, 1, 8, 3, 10}, {1}, {2, 9, 4}, {9, 5, 2, 6, 8, 7}, {6, 9,
4, 5}}
In[13]:= pickPath[lst] // Flatten // AbsoluteTiming
Out[13]= {0.0020001, {10, 10, 10, 10, 1, 9, 9, 9}}
Подход грубой силы Dreeves
argMax[f_, dom_List] :=
Module[{g}, g[e___] := g[e] = f[e];(*memoize*) dom[[Ordering[g /@ dom, -1]]]]
pick[x_] := argMax[-Length@Split[#] &, Tuples[x]]
In[14]:= pick[lst] // AbsoluteTiming
Out[14]= {0.7340420, {{10, 10, 10, 10, 1, 9, 9, 9}}}
В первый раз я использовал чуть более длинный список тестов. Подход с помощью грубой силы привел мой компьютер в виртуальную остановку, потребовав всю память, которая у него была. Довольно плохо. Мне пришлось перезагрузить через 10 минут. Перезапуск занял у меня еще четверть, потому что ПК стал очень не отвечающим.
Это мое мнение, и оно делает почти то же самое, что и Sjoerd, только в меньшем количестве кода.
LongestRuns[list_List] :=
Block[{gr, f = Intersection},
ReplaceRepeated[
list, {a___gr, Longest[e__List] /; f[e] =!= {}, b___} :> {a,
gr[e], b}] /.
gr[e__] :> ConstantArray[First[f[e]], Length[{e}]]]
Некоторая галерея:
In[497]:= LongestRuns[{{1, 2, 3}, {2, 3}, {1}, {1, 3, 4}, {4, 1}}]
Out[497]= {{2, 2}, {1, 1, 1}}
In[498]:= LongestRuns[{{3, 10, 6}, {8, 2, 10, 5, 9, 3, 6}, {3, 7, 10,
2, 8, 5, 9}, {6, 9, 1, 8, 3, 10}, {1}, {2, 9, 4}, {9, 5, 2, 6, 8,
7}, {6, 9, 4, 5}}]
Out[498]= {{3, 3, 3, 3}, {1}, {9, 9, 9}}
In[499]:= pickPath[{{3, 10, 6}, {8, 2, 10, 5, 9, 3, 6}, {3, 7, 10, 2,
8, 5, 9}, {6, 9, 1, 8, 3, 10}, {1}, {2, 9, 4}, {9, 5, 2, 6, 8,
7}, {6, 9, 4, 5}}]
Out[499]= {{10, 10, 10, 10}, {{1}, {9, 9, 9}}}
In[500]:= LongestRuns[{{2, 8}, {4, 2}, {3}, {9, 4, 6, 8, 2}, {5}, {8,
10, 6, 2, 3}, {9, 4, 6, 3, 10, 1}, {9}}]
Out[500]= {{2, 2}, {3}, {2}, {5}, {3, 3}, {9}}
In[501]:= LongestRuns[{{4, 6, 18, 15}, {1, 20, 16, 7, 14, 2, 9}, {12,
3, 15}, {17, 6, 13, 10, 3, 19}, {1, 15, 2, 19}, {5, 17, 3, 6,
14}, {5, 17, 9}, {15, 9, 19, 13, 8, 20}, {18, 13, 5}, {11, 5, 1,
12, 2}, {10, 4, 7}, {1, 2, 14, 9, 12, 3}, {9, 5, 19, 8}, {14, 1, 3,
4, 9}, {11, 13, 5, 1}, {16, 3, 7, 12, 14, 9}, {7, 4, 17, 18,
6}, {17, 19, 9}, {7, 15, 3, 12}, {19, 12, 5, 14, 8}, {1, 10, 12,
8}, {18, 16, 14, 19}, {2, 7, 10}, {19, 2, 5, 3}, {16, 17, 3}, {16,
2, 6, 20, 1, 3}, {12, 18, 11, 19, 17}, {12, 16, 9, 20, 4}, {19, 20,
10, 12, 9, 11}, {10, 12, 6, 19, 17, 5}}]
Out[501]= {{4}, {1}, {3, 3}, {1}, {5, 5}, {13, 13}, {1}, {4}, {9, 9,
9}, {1}, {7, 7}, {9}, {12, 12, 12}, {14}, {2, 2}, {3, 3}, {12, 12,
12, 12}}
РЕДАКТИРОВАТЬ, учитывая, что Сьерд-х Подход с использованием грубой силы Дривеса не работает на больших выборках из-за невозможности генерировать все кортежи одновременно, вот еще один подход с использованием грубой силы:
bfBestPick[e_List] := Block[{splits, gr, f = Intersection},
splits[{}] = {{}};
splits[list_List] :=
ReplaceList[
list, {a___gr, el__List /; f[el] =!= {},
b___} :> (Join[{a, gr[el]}, #] & /@ splits[{b}])];
Module[{sp =
Cases[splits[
e] //. {seq__gr,
re__List} :> (Join[{seq}, #] & /@ {re}), {__gr}, Infinity]},
sp[[First@Ordering[Length /@ sp, 1]]] /.
gr[args__] :> ConstantArray[First[f[args]], Length[{args}]]]]
Этот грубый выбор наилучшего выбора может привести к разным расщеплениям, но длина зависит от исходного вопроса.
test = {{4, 6, 18, 15}, {1, 20, 16, 7, 14, 2, 9}, {12, 3, 15}, {17, 6,
13, 10, 3, 19}, {1, 15, 2, 19}, {5, 17, 3, 6, 14}, {5, 17,
9}, {15, 9, 19, 13, 8, 20}, {18, 13, 5}, {11, 5, 1, 12, 2}, {10,
4, 7}, {1, 2, 14, 9, 12, 3}, {9, 5, 19, 8}, {14, 1, 3, 4, 9}, {11,
13, 5, 1}, {16, 3, 7, 12, 14, 9}, {7, 4, 17, 18, 6}, {17, 19,
9}, {7, 15, 3, 12}, {19, 12, 5, 14, 8}, {1, 10, 12, 8}, {18, 16,
14, 19}, {2, 7, 10}, {19, 2, 5, 3}, {16, 17, 3}, {16, 2, 6, 20, 1,
3}, {12, 18, 11, 19, 17}, {12, 16, 9, 20, 4}, {19, 20, 10, 12, 9,
11}, {10, 12, 6, 19, 17, 5}};
Пик не удается на этом примере.
In[637]:= Length[bfBestPick[test]] // Timing
Out[637]= {58.407, 17}
In[638]:= Length[LongestRuns[test]] // Timing
Out[638]= {0., 17}
In[639]:=
Length[Cases[pickPath[test], {__Integer}, Infinity]] // Timing
Out[639]= {0., 17}
Я публикую это на тот случай, если кто-то захочет найти контрпримеры, которые, например, в коде pickPath или LongestRuns действительно генерируют последовательность с наименьшим количеством прерываний.
Вот на это пошло...
runByN: для каждого номера показать, появляется ли он в каждом подсписке или нет
list= {{4, 2, 7, 5, 1, 9, 10}, {10, 1, 8, 3, 2, 7}, {9, 2, 7, 3, 6, 4, 5}, {10, 3, 6, 4, 8, 7}, {7}, {3, 1, 8, 2, 4, 7, 10, 6}, {7, 6}, {10, 2, 8, 5, 6, 9, 7, 3}, {1, 4, 8}, {5, 6, 1}, {3, 2, 1}, {10,6, 4}, {10, 7, 3}, {10, 2, 4}, {1, 3, 5, 9, 7, 4, 2, 8}, {7, 1, 3}, {5, 7, 1, 10, 2, 3, 6, 8}, {10, 8, 3, 6, 9, 4, 5, 7}, {3, 10, 5}, {1}, {7, 9, 1, 6, 2, 4}, {9, 7, 6, 2}, {5, 6, 9, 7}, {1, 5}, {1,9, 7, 5, 4}, {5, 4, 9, 3, 1, 7, 6, 8}, {6}, {10}, {6}, {7, 9}};
runsByN = Transpose[Table[If[MemberQ[#, n], n, 0], {n, Max[list]}] & /@ list]
Out = {{1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0,1, 1, 1, 0, 0, 0, 0}, {2, 2, 2, 0, 0, 2, 0, 2, 0, 0, 2, 0, 0, 2, 2,0, 2, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0}, {0, 3, 3, 3, 0, 3, 0,3, 0, 0, 3, 0, 3, 0, 3, 3, 3, 3, 3, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0,0}, {4, 0, 4, 4, 0, 4, 0, 0, 4, 0, 0, 4, 0, 4, 4, 0, 0, 4, 0, 0, 4, 0, 0, 0, 4, 4, 0, 0, 0, 0}, {5, 0, 5, 0, 0, 0, 0, 5, 0, 5, 0, 0, 0, 0, 5, 0, 5, 5, 5, 0, 0, 0, 5, 5, 5, 5, 0, 0, 0, 0}, {0, 0, 6, 6, 0, 6, 6, 6, 0, 6, 0, 6, 0, 0, 0, 0, 6, 6, 0, 0, 6, 6, 6, 0, 0, 6, 6, 0,6, 0}, {7, 7, 7, 7, 7, 7, 7, 7, 0, 0, 0, 0, 7, 0, 7, 7, 7, 7, 0, 0, 7, 7, 7, 0, 7, 7, 0, 0, 0, 7}, {0, 8, 0, 8, 0, 8, 0, 8, 8, 0, 0, 0, 0, 0, 8, 0, 8, 8, 0, 0, 0, 0, 0, 0, 0, 8, 0, 0, 0, 0}, {9, 0, 9, 0, 0, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9, 0, 0, 9, 0, 0, 9, 9, 9, 0, 9, 9, 0, 0, 0, 9}, {10, 10, 0, 10, 0, 10, 0, 10, 0, 0, 0, 10, 10, 10, 0, 0, 10, 10, 10, 0, 0, 0, 0, 0, 0, 0, 0, 10, 0, 0}};
runsByN является list транспонированный, с нулями, вставленными для обозначения пропущенных чисел. Это показывает подсписки, в которых появились 1, 2, 3 и 4.
myPick: выбор чисел, составляющих оптимальный путь
myPick Рекурсивно строит список самых длинных трасс. Он ищет не все оптимальные решения, а первое решение минимальной длины.
myPick[{}, c_] := Flatten[c]
myPick[l_, c_: {}] :=
Module[{r = Length /@ (l /. {x___, 0, ___} :> {x}), m}, m = Max[r];
myPick[Cases[(Drop[#, m]) & /@ l, Except[{}]],
Append[c, Table[Position[r, m, 1, 1][[1, 1]], {m}]]]]
choices = myPick[runsByN]
(* Out= {7, 7, 7, 7, 7, 7, 7, 7, 1, 1, 1, 10, 10, 10, 3, 3, 3, 3, 3, 1, 1, 6, 6, 1, 1, 1, 6, 10, 6, 7} *)
Спасибо Mr.Wizard за предложение использовать правило замены в качестве эффективной альтернативы TakeWhile,
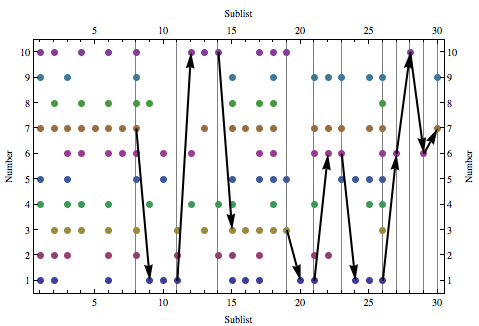
Эпилог: Визуализация пути решения
runsPlot[choices1_, runsN_] :=
Module[{runs = {First[#], Length[#]} & /@ Split[choices1], myArrow,
m = Max[runsN]},
myArrow[runs1_] :=
Module[{data1 = Reverse@First[runs1], data2 = Reverse[runs1[[2]]],
deltaX},
deltaX := data2[[1]] - 1;
myA[{}, _, out_] := out;
myA[inL_, deltaX_, outL_] :=
Module[{data3 = outL[[-1, 1, 2]]},
myA[Drop[inL, 1], inL[[1, 2]] - 1,
Append[outL, Arrow[{{First[data3] + deltaX,
data3[[2]]}, {First[data3] + deltaX + 1, inL[[1, 1]]}}]]]];
myA[Drop[runs1, 2], deltaX, {Thickness[.005],
Arrow[{data1, {First[data1] + 1, data2[[2]]}}]}]];
ListPlot[runsN,
Epilog -> myArrow[runs],
PlotStyle -> PointSize[Large],
Frame -> True,
PlotRange -> {{1, Length[choices1]}, {1, m}},
FrameTicks -> {All, Range[m]},
PlotRangePadding -> .5,
FrameLabel -> {"Sublist", "Number", "Sublist", "Number"},
GridLines :> {FoldList[Plus, 0, Length /@ Split[choices1]], None}
]];
runsPlot[choices, runsByN]
На приведенной ниже диаграмме представлены данные list, Каждая построенная точка соответствует номеру и подсписку, в котором это произошло.
Итак, вот мой "один вкладыш" с улучшениями от Mr.Wizard:
pickPath[lst_List] :=
Module[{M = Fold[{#2, #} &, {{}}, Reverse@lst]},
Reap[While[M != {{}},
Do[Sow@#[[-2,1]], {Length@# - 1}] &@
NestWhileList[# ⋂ First[M = Last@M] &, M[[1]], # != {} &]
]][[2, 1]]
]
Он в основном использует пересечение несколько раз в последовательных списках, пока не появится пустой, а затем делает это снова и снова. В огромном испытании на пытки с
M = Table[RandomSample[Range[1000], RandomInteger[{1, 200}]], {1000}];
я получил Timing[] постоянно около 0,032 на моем 2 ГГц Core 2 Duo.
Ниже этого пункта - моя первая попытка, которую я оставлю для вашего ознакомления.
Для заданного списка списков элементов M мы подсчитываем различные элементы и количество списков, перечисляем различные элементы в каноническом порядке и строим матрицу K[i,j] детализируя присутствие элемента i в списке j:
elements = Length@(Union @@ M);
lists = Length@M;
eList = Union @@ M;
positions = Flatten@Table[{i, Sequence @@ First@Position[eList, M[[i,j]]} -> 1,
{i, lists},
{j, Length@M[[i]]}];
K = Transpose@Normal@SparseArray@positions;
Теперь проблема эквивалентна обходу этой матрицы слева направо, только наступая на 1 и изменяя строки как можно меньше раз.
Чтобы достичь этого я Sort строки, возьмите одну из самых последовательных 1 в начале, отследите, какой элемент я выбрал, Drop что много столбцов из K и повторить:
R = {};
While[Length@K[[1]] > 0,
len = LengthWhile[K[[row = Last@Ordering@K]], # == 1 &];
Do[AppendTo[R, eList[[row]]], {len}];
K = Drop[#, len] & /@ K;
]
Это имеет AbsoluteTiming примерно в три раза больше, чем у Sjoerd C. de Vries.
Неделя вышла! Вот легендарное решение от Карла Волля. (Я пытался заставить его опубликовать это сам. Карл, если вы сталкиваетесь с этим и хотите взять официальный кредит, просто вставьте его как отдельный ответ, и я удалю этот!)
pick[data_] := Module[{common,tmp},
common = {};
tmp = Reverse[If[(common = Intersection[common,#])=={}, common = #, common]& /@
data];
common = .;
Reverse[If[MemberQ[#, common], common, common = First[#]]& /@ tmp]]
Все еще цитирую Карла:
По сути, вы начинаете с самого начала и находите элемент, который дает вам самую длинную строку общих элементов. Как только строка больше не может быть расширена, начните новую строку. Мне кажется, что этот алгоритм должен дать вам правильный ответ (есть много правильных ответов).
Может использовать целочисленное линейное программирование. Вот код для этого.
bestPick[lists_] := Module[
{picks, span, diffs, v, dv, vars, diffvars, fvars,
c1, c2, c3, c4, constraints, obj, res},
span = Max[lists] - Min[lists];
vars = MapIndexed[v[Sequence @@ #2] &, lists, {2}];
picks = Total[vars*lists, {2}];
diffs = Differences[picks];
diffvars = Array[dv, Length[diffs]];
fvars = Flatten[{vars, diffvars}];
c1 = Map[Total[#] == 1 &, vars];
c2 = Map[0 <= # <= 1 &, fvars];
c3 = Thread[span*diffvars >= diffs];
c4 = Thread[span*diffvars >= -diffs];
constraints = Join[c1, c2, c3, c4];
obj = Total[diffvars];
res = Minimize[{obj, constraints}, fvars, Integers];
{res[[1]], Flatten[vars*lists /. res[[2]] /. 0 :> Sequence[]]}
]
Ваш пример:
lists = {{1, 2, 3}, {2, 3}, {1}, {1, 3, 4}, {4, 1}}
bestPick[lists]
Out [88] = {1, {2, 2, 1, 1, 1}}
При больших проблемах Minimum может столкнуться с проблемами, поскольку использует точные методы для решения расслабленных LP. В этом случае вам может потребоваться переключиться на NMinimize и изменить аргумент домена на ограничение вида Element[fvars,Integers].
Даниэль Лихтблау