Вычислить ограничивающий многоугольник альфа-формы из триангуляции Делоне
Для заданного набора точек на плоскости понятие альфа-формы для заданного положительного числа альфа определяется путем нахождения триангуляции Делоне и удаления любых треугольников, для которых хотя бы один край превышает альфа по длине. Вот пример использования d3:
http://bl.ocks.org/gka/1552725
Проблема в том, что, когда есть тысячи точек, просто нарисовать все внутренние треугольники слишком медленно для интерактивной визуализации, поэтому я хотел бы просто найти ограничивающие полигоны. Это не так просто, потому что, как видно из этого примера, иногда может быть два таких многоугольника.
В качестве упрощения предположим, что была проведена некоторая кластеризация, так что гарантированно будет уникальный ограничивающий многоугольник для каждой триангуляции. Какой лучший способ найти этот ограничивающий многоугольник? В частности, края должны быть упорядочены последовательно, и это должно поддерживать возможность "дырок" (представьте себе форму тора или пончика - это можно выразить в GeoJSON).
4 ответа
Создайте граф, в котором узлы соответствуют треугольникам Делоне и в котором есть ребро графа между двумя треугольниками тогда и только тогда, когда они разделяют две вершины.
Вычислить связанные компоненты графика.
Для каждого подключенного компонента найдите все узлы, которые имеют менее трех смежных узлов (то есть те, которые имеют степень 0, 1 или 2). Они соответствуют граничным треугольникам. Мы определяем ребра граничного треугольника, которые не являются общими с другим треугольником, как граничные ребра этого граничного треугольника.
В качестве примера я выделил эти граничные треугольники в вашем примере "вопросительный знак" триангуляции Делоне:
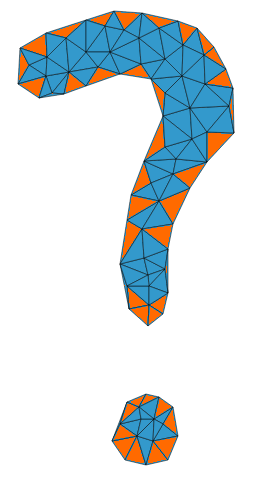
По определению каждый граничный треугольник смежен не более чем с двумя другими граничными треугольниками. Граничные ребра граничных треугольников образуют циклы. Вы можете просто пройти эти циклы, чтобы определить формы многоугольников для границ. Это также будет работать для полигонов с отверстиями, если вы будете помнить об этом в своей реализации.
Вот код Python, который делает то, что вам нужно. Я изменил вычисление альфа-формы (вогнутой оболочки), чтобы он не вставлял внутренние ребра (only_outer параметр). Я также сделал его автономным, чтобы он не зависел от внешней библиотеки.
from scipy.spatial import Delaunay
import numpy as np
def alpha_shape(points, alpha, only_outer=True):
"""
Compute the alpha shape (concave hull) of a set of points.
:param points: np.array of shape (n,2) points.
:param alpha: alpha value.
:param only_outer: boolean value to specify if we keep only the outer border
or also inner edges.
:return: set of (i,j) pairs representing edges of the alpha-shape. (i,j) are
the indices in the points array.
"""
assert points.shape[0] > 3, "Need at least four points"
def add_edge(edges, i, j):
"""
Add a line between the i-th and j-th points,
if not in the list already
"""
if (i, j) in edges or (j, i) in edges:
# already added
assert (j, i) in edges, "Can't go twice over same directed edge right?"
if only_outer:
# if both neighboring triangles are in shape, it's not a boundary edge
edges.remove((j, i))
return
edges.add((i, j))
tri = Delaunay(points)
edges = set()
# Loop over triangles:
# ia, ib, ic = indices of corner points of the triangle
for ia, ib, ic in tri.vertices:
pa = points[ia]
pb = points[ib]
pc = points[ic]
# Computing radius of triangle circumcircle
# www.mathalino.com/reviewer/derivation-of-formulas/derivation-of-formula-for-radius-of-circumcircle
a = np.sqrt((pa[0] - pb[0]) ** 2 + (pa[1] - pb[1]) ** 2)
b = np.sqrt((pb[0] - pc[0]) ** 2 + (pb[1] - pc[1]) ** 2)
c = np.sqrt((pc[0] - pa[0]) ** 2 + (pc[1] - pa[1]) ** 2)
s = (a + b + c) / 2.0
area = np.sqrt(s * (s - a) * (s - b) * (s - c))
circum_r = a * b * c / (4.0 * area)
if circum_r < alpha:
add_edge(edges, ia, ib)
add_edge(edges, ib, ic)
add_edge(edges, ic, ia)
return edges
Если вы запустите его со следующим тестовым кодом, вы получите этот рисунок:
from matplotlib.pyplot import *
# Constructing the input point data
np.random.seed(0)
x = 3.0 * np.random.rand(2000)
y = 2.0 * np.random.rand(2000) - 1.0
inside = ((x ** 2 + y ** 2 > 1.0) & ((x - 3) ** 2 + y ** 2 > 1.0) & ((x - 1.5) ** 2 + y ** 2 > 0.09))
points = np.vstack([x[inside], y[inside]]).T
# Computing the alpha shape
edges = alpha_shape(points, alpha=0.25, only_outer=True)
# Plotting the output
figure()
axis('equal')
plot(points[:, 0], points[:, 1], '.')
for i, j in edges:
plot(points[[i, j], 0], points[[i, j], 1])
show()
Я знаю, что это отложенный ответ, но методы, опубликованные здесь, не помогли мне по разным причинам.
Упомянутый пакет Alphashape в целом хорош, но его недостатком является то, что он использует методы Shapely cascade_union и triangulation, чтобы дать вам окончательный вогнутый корпус, который очень медленный для больших наборов данных и низких значений альфа (высокая точность). В этом случае код, опубликованный Иддо Ханниэлем (и ревизия Гарольда), сохранит большое количество ребер внутри, и единственный способ растворить их - использовать вышеупомянутые cascade_union и triangulation от Shapely.
Обычно я работаю со сложными формами, и приведенный ниже код работает нормально и быстро (2 секунды для 100 000 2D-точек):
import numpy as np
from shapely.geometry import MultiLineString
from shapely.ops import unary_union, polygonize
from scipy.spatial import Delaunay
from collections import Counter
from math import sqrt
def concave_hull(coords, alpha): # coords is a 2D numpy array
# i removed the Qbb option from the scipy defaults.
# it is much faster and equally precise without it.
# unless your coords are integers.
# see http://www.qhull.org/html/qh-optq.htm
tri = Delaunay(coords, qhull_options='Qc Qz Q12').vertices
ia, ib, ic = tri[:, 0], tri[:, 1], tri[:, 2] # indices of each of the triangles' points
pa, pb, pc = coords[ia], coords[ib], coords[ic] # coordinates of each of the triangles' points
a = np.sqrt((pa[:, 0] - pb[:, 0]) ** 2 + (pa[:, 1] - pb[:, 1]) ** 2)
b = np.sqrt((pb[:, 0] - pc[:, 0]) ** 2 + (pb[:, 1] - pc[:, 1]) ** 2)
c = np.sqrt((pc[:, 0] - pa[:, 0]) ** 2 + (pc[:, 1] - pa[:, 1]) ** 2)
s = (a + b + c) * 0.5 # Semi-perimeter of triangle
area = np.sqrt(s * (s - a) * (s - b) * (s - c)) # Area of triangle by Heron's formula
filter = a * b * c / (4. * area) < 1. / alpha # Radius Filter based on alpha value
# Filter the edges
edges = tri[filter]
# now a main difference with the aforementioned approaches is that we dont use a Set()
# because this eliminates duplicate edges.
# in the list below both (i, j) and (j, i) pairs are counted. The reasoning is that
# boundary edges appear only once while interior edges twice
edges = [tuple(sorted(combo)) for e in edges for combo in itertools.combinations(e, 2)]
count = Counter(edges) # count occurrences of each edge
# keep only edges that appear one time (concave hull edges)
edges = [e for e, c in count.items() if c == 1]
# these are the coordinates of the edges that comprise the concave hull
edges = [(points[e[0]], points[e[1]]) for e in edges ]
# use this only if you need to return your hull points in "order" (i think its CCW)
ml = MultiLineString(unique_edges)
poly = polygonize(ml)
hull = unary_union(list(poly))
hull_vertices = boundary.exterior.coords.xy
return edges, hull_vertices
Теперь существует пакет python alphashape, который чрезвычайно прост в использовании и может быть установлен с помощьюpip или conda.
Функция main имеет входные данные, аналогичные ответу @Iddo Hanniel, настройка второго позиционного аргумента даст вам желаемый план. В качестве альтернативы вы можете оставить второй позиционный аргумент пустым, и функция оптимизирует этот параметр для вас, чтобы получить лучший вогнутый корпус. Остерегайтесь, время вычислений значительно увеличится, если вы позволите функции оптимизировать значение.
Слегка пересмотрите ответ Ханниэля для случая трехмерной точки (тетраэдр).
def alpha_shape(points, alpha, only_outer=True):
"""
Compute the alpha shape (concave hull) of a set of points.
:param points: np.array of shape (n, 3) points.
:param alpha: alpha value.
:param only_outer: boolean value to specify if we keep only the outer border
or also inner edges.
:return: set of (i,j) pairs representing edges of the alpha-shape. (i,j) are
the indices in the points array.
"""
assert points.shape[0] > 3, "Need at least four points"
def add_edge(edges, i, j):
"""
Add a line between the i-th and j-th points,
if not in the set already
"""
if (i, j) in edges or (j, i) in edges:
# already added
if only_outer:
# if both neighboring triangles are in shape, it's not a boundary edge
if (j, i) in edges:
edges.remove((j, i))
return
edges.add((i, j))
tri = Delaunay(points)
edges = set()
# Loop over triangles:
# ia, ib, ic, id = indices of corner points of the tetrahedron
print(tri.vertices.shape)
for ia, ib, ic, id in tri.vertices:
pa = points[ia]
pb = points[ib]
pc = points[ic]
pd = points[id]
# Computing radius of tetrahedron Circumsphere
# http://mathworld.wolfram.com/Circumsphere.html
pa2 = np.dot(pa, pa)
pb2 = np.dot(pb, pb)
pc2 = np.dot(pc, pc)
pd2 = np.dot(pd, pd)
a = np.linalg.det(np.array([np.append(pa, 1), np.append(pb, 1), np.append(pc, 1), np.append(pd, 1)]))
Dx = np.linalg.det(np.array([np.array([pa2, pa[1], pa[2], 1]),
np.array([pb2, pb[1], pb[2], 1]),
np.array([pc2, pc[1], pc[2], 1]),
np.array([pd2, pd[1], pd[2], 1])]))
Dy = - np.linalg.det(np.array([np.array([pa2, pa[0], pa[2], 1]),
np.array([pb2, pb[0], pb[2], 1]),
np.array([pc2, pc[0], pc[2], 1]),
np.array([pd2, pd[0], pd[2], 1])]))
Dz = np.linalg.det(np.array([np.array([pa2, pa[0], pa[1], 1]),
np.array([pb2, pb[0], pb[1], 1]),
np.array([pc2, pc[0], pc[1], 1]),
np.array([pd2, pd[0], pd[1], 1])]))
c = np.linalg.det(np.array([np.array([pa2, pa[0], pa[1], pa[2]]),
np.array([pb2, pb[0], pb[1], pb[2]]),
np.array([pc2, pc[0], pc[1], pc[2]]),
np.array([pd2, pd[0], pd[1], pd[2]])]))
circum_r = math.sqrt(math.pow(Dx, 2) + math.pow(Dy, 2) + math.pow(Dz, 2) - 4 * a * c) / (2 * abs(a))
if circum_r < alpha:
add_edge(edges, ia, ib)
add_edge(edges, ib, ic)
add_edge(edges, ic, id)
add_edge(edges, id, ia)
add_edge(edges, ia, ic)
add_edge(edges, ib, id)
return edges
Оказывается, у TopoJSON есть алгоритм слияния, который выполняет именно эту задачу: https://github.com/mbostock/topojson/wiki/API-Reference
Есть даже пример, показывающий это в действии: http://bl.ocks.org/mbostock/9927735
В моем случае мне было легко генерировать данные TopoJSON, и эта библиотечная функция отлично справилась с задачей.
Основываясь на ответе @ Тимоти, я использовал следующий алгоритм для вычисления граничных колец триангуляции Делоне.
from matplotlib.tri import Triangulation
import numpy as np
def get_boundary_rings(x, y, elements):
mpl_tri = Triangulation(x, y, elements)
idxs = np.vstack(list(np.where(mpl_tri.neighbors == -1))).T
unique_edges = list()
for i, j in idxs:
unique_edges.append((mpl_tri.triangles[i, j],
mpl_tri.triangles[i, (j+1) % 3]))
unique_edges = np.asarray(unique_edges)
ring_collection = list()
initial_idx = 0
for i in range(1, len(unique_edges)-1):
if unique_edges[i-1, 1] != unique_edges[i, 0]:
try:
idx = np.where(
unique_edges[i-1, 1] == unique_edges[i:, 0])[0][0]
unique_edges[[i, idx+i]] = unique_edges[[idx+i, i]]
except IndexError:
ring_collection.append(unique_edges[initial_idx:i, :])
initial_idx = i
continue
# if there is just one ring, the exception is never reached,
# so populate ring_collection before returning.
if len(ring_collection) == 0:
ring_collection.append(np.asarray(unique_edges))
return ring_collection
Альфа-формы определяются как триангуляция Делоне без ребер, превышающих альфа. Сначала удалите все внутренние треугольники, а затем все ребра, превышающие альфа.