Создать равный аспект (квадратный) график с несколькими осями, когда пределы данных разные?

Question

Я хотел бы создать квадратный график, используя несколько осей, используя make_axes_locateable как продемонстрировано в документации matplotlib. Однако, хотя это работает на графиках, где данные x и y имеют одинаковый диапазон, оно не работает, когда диапазоны отличаются на несколько порядков.

import numpy as np
import matplotlib.pyplot as plt

from mpl_toolkits.axes_grid1 import make_axes_locatable

x = np.random.normal(512, 112, 240)
y = np.random.normal(0.5, 0.1, 240)

_, ax = plt.subplots()
divider = make_axes_locatable(ax)

xhax = divider.append_axes("top", size=1, pad=0.1, sharex=ax)
yhax = divider.append_axes("right", size=1, pad=0.1, sharey=ax)

ax.scatter(x, y)
xhax.hist(x)
yhax.hist(y, orientation="horizontal")

x0,x1 = ax.get_xlim()
y0,y1 = ax.get_ylim()
ax.set_aspect(abs(x1-x0)/abs(y1-y0))

plt.show()

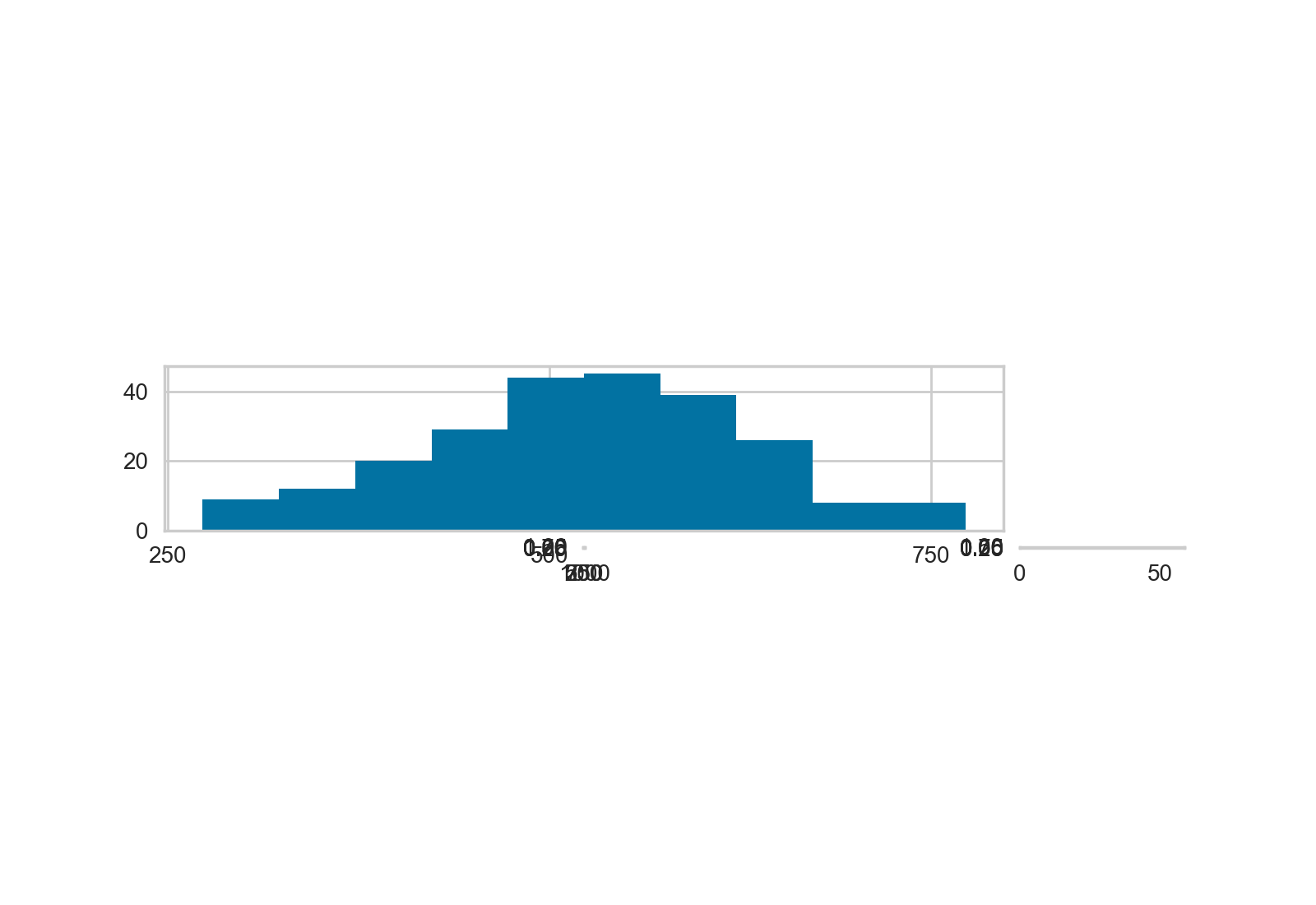
Хотя этот код использует set_aspect ответ как в Как сделать квадрат рассеяния Matplotlib? оси не изменены правильно, как показано здесь:

Я попытался исправить это с:

ax.set_aspect(abs(x1-x0)/abs(y1-y0), share=True)

Но это привело к следующему:

Установка аспекта после вызова scatter и до создания двух осей гистограммы, похоже, не имела никакого эффекта, даже если кажется, что это было сделано в примере документации. Этот код работает, когда диапазон данных одинаков:

Обновление: одним из ключевых ограничений этого вопроса является использование make_axes_locateable и не GridSpec как обсуждено в комментариях ниже. Проблема, над которой я работаю, заключается в создании функций построения, которые принимают объект Axes для работы и изменяют его, не зная фигуру или любые другие оси в графике, как в следующем коде:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as grid

from mpl_toolkits.axes_grid1 import make_axes_locatable, axes_size


def joint_plot(x, y, ax=None):
    """
    Create a square joint plot of x and y.
    """
    if ax is None:
        ax = plt.gca()

    divider = make_axes_locatable(ax)
    xhax = divider.append_axes("top", size=1, pad=0.1, sharex=ax)
    yhax = divider.append_axes("right", size=1, pad=0.1, sharey=ax)

    ax.scatter(x, y)
    xhax.hist(x)
    yhax.hist(y, orientation="horizontal")

    x0,x1 = ax.get_xlim()
    y0,y1 = ax.get_ylim()
    ax.set_aspect(abs(x1-x0)/abs(y1-y0))

    plt.sca(ax)
    return ax, xhax, yhax


def color_plot(x, y, colors, ax=None):
    if ax is None:
        ax = plt.gca()

    divider = make_axes_locatable(ax)
    cbax = divider.append_axes("right", size="5%", pad=0.1)

    sc = ax.scatter(x, y, marker='o', c=colors, cmap='RdBu')
    plt.colorbar(sc, cax=cbax)

    ax.set_aspect("equal")

    plt.sca(ax)
    return ax, cbax


if __name__ == "__main__":
    _, axes = plt.subplots(nrows=2, ncols=2, figsize=(9,6))

    # Plot 1
    x = np.random.normal(100, 17, 120)
    y = np.random.normal(0.5, 0.1, 120)
    joint_plot(x, y, axes[0,0])

    # Plot 2
    x = np.random.normal(100, 17, 120)
    y = np.random.normal(100, 17, 120)
    c = np.random.normal(100, 17, 120)
    color_plot(x, y, c, axes[0,1])

    # Plot 3
    x = np.random.normal(100, 17, 120)
    y = np.random.normal(0.5, 0.1, 120)
    c = np.random.uniform(0.0, 1.0, 120)
    color_plot(x, y, c, axes[1,0])

    # Plot 4
    x = np.random.normal(0.5, 0.1, 120)
    y = np.random.normal(0.5, 0.1, 120)
    joint_plot(x, y, axes[1,1])

    plt.tight_layout()
    plt.show()

Этот вопрос расширяет такие вопросы, как Задать равный аспект на графике с цветовой шкалой и взаимодействие Python между осью ("квадрат") и set_xlim из-за ограничения только для осей.

Answer 1

Одним из способов решения этой проблемы является сохранение пределов данных по осям X и Y равными. Это может быть сделано путем нормализации значений, скажем, между 0 и 1. Таким образом, команда ax.set_aspect('equal') работает как положено. Конечно, если это сделать только один, метки тиков будут только в диапазоне от 0 до 1, поэтому нужно применить немного магии matplotlib, чтобы настроить метки тиков в соответствии с исходным диапазоном данных. Ответ здесь показывает, как это можно сделать с помощью FuncFormatter, Однако в качестве исходных тиков выбираются относительно интервала [0,1], используя FuncFormatter одно только приведет к нечетным тикам, например, если коэффициент равен 635, исходный тик 0,2 станет 127. Чтобы получить "хорошие" тики, можно дополнительно использовать AutoLocator, который может вычислить тики для исходного диапазона данных с tick_values() функция. Затем эти отметки можно снова масштабировать до интервала [0,1], а затем FuncFormatter можете вычислить метки Это немного сложновато, но в итоге требуется всего около 10 строк дополнительного кода:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker

from mpl_toolkits.axes_grid1 import make_axes_locatable

x = np.random.normal(512, 112, 240)
y = np.random.normal(0.5, 0.1, 240)


fig,ax=plt.subplots()

divider = make_axes_locatable(ax)


##increased pad from 0.1 to 0.2 so that tick labels don't overlap
xhax = divider.append_axes("top", size=1, pad=0.2, sharex=ax)
yhax = divider.append_axes("right", size=1, pad=0.2, sharey=ax)

##'normalizing' x and y values to be between 0 and 1:
xn = (x-min(x))/(max(x)-min(x))
yn = (y-min(y))/(max(y)-min(y))

##producinc the plots
ax.scatter(xn, yn)
xhax.hist(xn)
yhax.hist(yn, orientation="horizontal")

##turning off duplicate ticks (if needed):
plt.setp(xhax.get_xticklabels(), visible=False)
plt.setp(yhax.get_yticklabels(), visible=False)

ax.set_aspect('equal')


##setting up ticks and labels to simulate real data:
locator = mticker.AutoLocator()

xticks = (locator.tick_values(min(x),max(x))-min(x))/(max(x)-min(x))
ax.set_xticks(xticks)
ax.xaxis.set_major_formatter(mticker.FuncFormatter(
    lambda t, pos: '{0:g}'.format(t*(max(x)-min(x))+min(x))
))

yticks = (locator.tick_values(min(y),max(y))-min(y))/(max(y)-min(y))
ax.set_yticks(yticks)
ax.yaxis.set_major_formatter(mticker.FuncFormatter(
    lambda t, pos: '{0:g}'.format(t*(max(y)-min(y))+min(y))
))

fig.tight_layout()
plt.show()

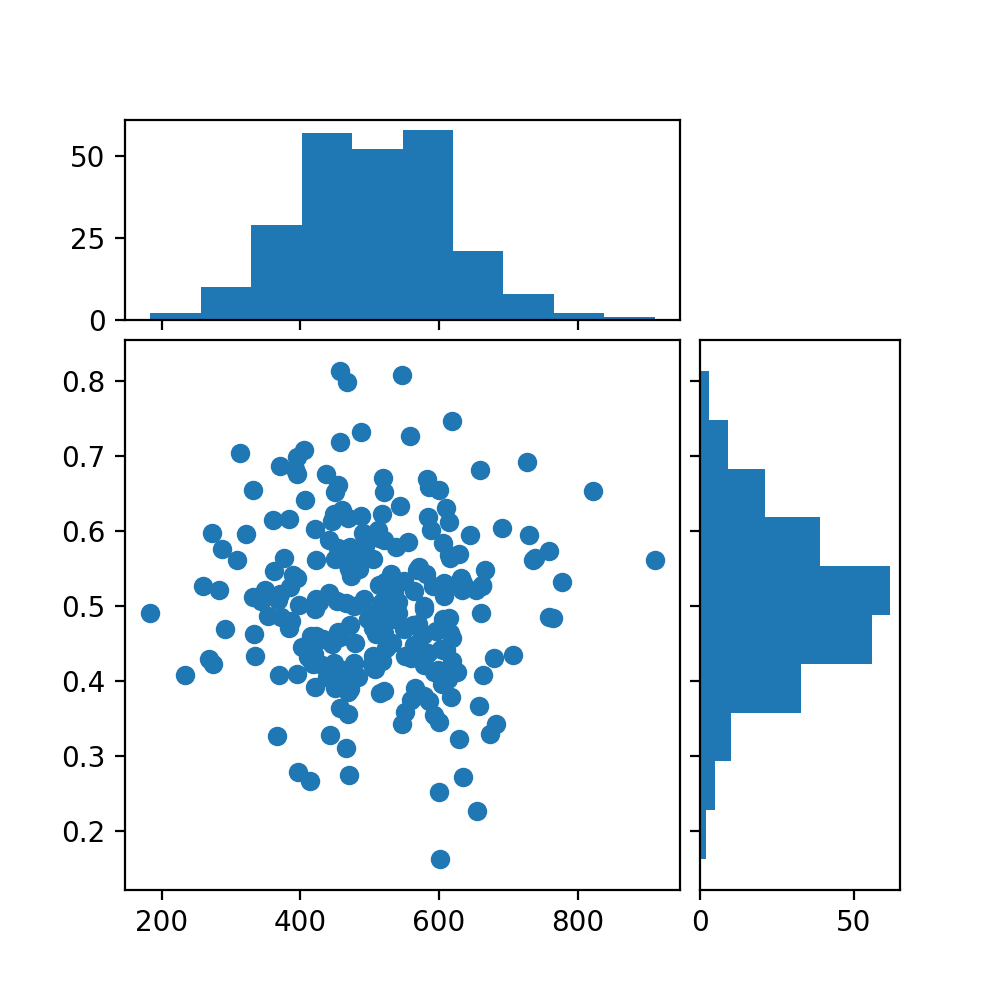
Полученное изображение выглядит ожидаемым и остается квадратным даже при изменении размера изображения.

Старый ответ:

Это скорее обходной путь, чем решение:

Вместо того, чтобы использовать ax.set_aspect() Вы можете настроить свою фигуру так, чтобы она была квадратной, предоставляя figsize=(n,n) в plt.subplots, где n будет ширина и высота в дюймах. Как высота xhax и ширина yhax оба 1 дюйм, это означает, что ax также становится квадратным.

import numpy as np
import matplotlib.pyplot as plt

from mpl_toolkits.axes_grid1 import make_axes_locatable

x = np.random.normal(512, 112, 240)
y = np.random.normal(0.5, 0.1, 240)

fig, ax = plt.subplots(figsize=(5,5))

divider = make_axes_locatable(ax)

xhax = divider.append_axes("top", size=1, pad=0.1, sharex=ax)
yhax = divider.append_axes("right", size=1, pad=0.1, sharey=ax)

ax.scatter(x, y)
xhax.hist(x)
yhax.hist(y, orientation="horizontal")

##turning off duplicate ticks:
plt.setp(xhax.get_xticklabels(), visible=False)
plt.setp(yhax.get_yticklabels(), visible=False)

plt.show()

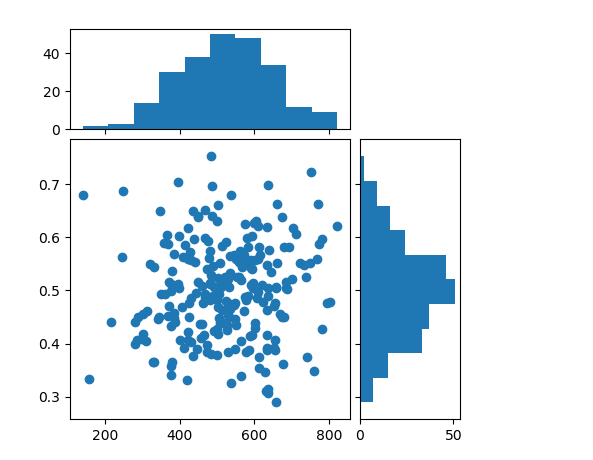
Результат выглядит так:

Конечно, как только вы измените размер фигуры, квадратный аспект исчезнет. Но если вы уже знаете окончательный размер вашей фигуры и просто хотите сохранить ее для дальнейшего использования, это должно быть достаточно быстрым решением.

Answer 2

axes_grid1 "s Divider работает немного иначе, чем обычные сюжеты. Он не может напрямую справляться с аспектами, потому что размер осей определяется во время прорисовки либо в относительных, либо в абсолютных координатах.

При желании вы можете вручную указать размер осей в абсолютных координатах, чтобы получить квадратный участок.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable, axes_size

x = np.random.normal(512, 112, 240)
y = np.random.normal(0.5, 0.1, 240)

_, ax = plt.subplots()
divider = make_axes_locatable(ax)

xhax = divider.append_axes("top", size=1, pad=0.1, sharex=ax)
yhax = divider.append_axes("right", size=1, pad=0.1, sharey=ax)

horiz = [axes_size.Fixed(2.8), axes_size.Fixed(.1), axes_size.Fixed(1)]
vert = [axes_size.Fixed(2.8), axes_size.Fixed(.1), axes_size.Fixed(1)]
divider.set_horizontal(horiz)
divider.set_vertical(vert)

ax.scatter(x, y)
xhax.hist(x)
yhax.hist(y, orientation="horizontal")

plt.setp(xhax.get_xticklabels(), visible=False)
plt.setp(yhax.get_yticklabels(), visible=False)

plt.show()

Это решение устойчиво к изменениям размера фигуры в том смысле, что сетка всегда имеет ширину 2,8 + 0,1 + 1 = 3,9 дюйма и высоту. Так что нужно просто убедиться, что размер фигуры всегда достаточно велик для размещения сетки. В противном случае это может обрезать маргинальные участки и выглядеть так:

Чтобы иметь адаптивное решение, которое по-прежнему масштабируется с размером фигуры, можно определить Size, которая берет остаток от абсолютных размеров отступов и краевых осей и возвращает минимум из них в абсолютных координатах (дюймах) для обоих направлений, так что оси всегда квадратные.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.transforms import Bbox
from mpl_toolkits.axes_grid1 import make_axes_locatable, axes_size

class RemainderFixed(axes_size.Scaled):
    def __init__(self, xsizes, ysizes, divider):
        self.xsizes =xsizes
        self.ysizes =ysizes
        self.div = divider

    def get_size(self, renderer):
        xrel, xabs = axes_size.AddList(self.xsizes).get_size(renderer)
        yrel, yabs = axes_size.AddList(self.ysizes).get_size(renderer)
        bb = Bbox.from_bounds(*self.div.get_position()).transformed(self.div._fig.transFigure)
        w = bb.width/self.div._fig.dpi - xabs
        h = bb.height/self.div._fig.dpi - yabs
        return 0, min([w,h])

x = np.random.normal(512, 112, 240)
y = np.random.normal(0.5, 0.1, 240)

fig, ax = plt.subplots()
divider = make_axes_locatable(ax)

margin_size = axes_size.Fixed(1)
pad_size = axes_size.Fixed(.1)
xsizes = [pad_size, margin_size]
ysizes = xsizes

xhax = divider.append_axes("top", size=margin_size, pad=pad_size, sharex=ax)
yhax = divider.append_axes("right", size=margin_size, pad=pad_size, sharey=ax)

divider.set_horizontal([RemainderFixed(xsizes, ysizes, divider)] + xsizes)
divider.set_vertical([RemainderFixed(xsizes, ysizes, divider)] + ysizes)

ax.scatter(x, y)
xhax.hist(x)
yhax.hist(y, orientation="horizontal")

plt.setp(xhax.get_xticklabels(), visible=False)
plt.setp(yhax.get_yticklabels(), visible=False)

plt.show()

Обратите внимание, что размеры полей всегда равны 1 дюйму, независимо от размера фигуры, как оси рассеяния подгоняются к оставшемуся пространству и остаются квадратными.