Python взаимодействие между осью ('квадрат') и set_xlim

Question

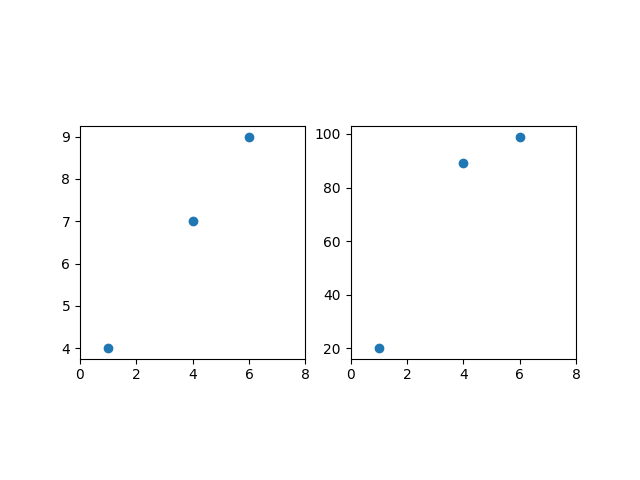
Для графика корреляции я хотел бы иметь график, который является оптически квадратным (такой же длины x и y в пикселях), но также имеет определенный предел оси для x и y. Я могу получить каждый из 2 отдельно, но не одновременно:

import matplotlib.pyplot as plt

f, (ax1, ax2) = plt.subplots(1, 2)
x = [1 , 4 , 6]
y1 = [4, 7, 9]
y2 = [20, 89, 99]

ax1.plot(x, y1, 'o')
ax2.plot(x, y2, 'o')

myXlim = [0, 8]
ax1.set_xlim(myXlim)
ax2.set_xlim(myXlim)

ax1.axis('square')
ax2.axis('square')
# limit is gone here

ax1.set_xlim(myXlim)
ax2.set_xlim(myXlim)
# square is gone here

plt.show()

Если я просто использую ax1.set_xlim(myXlim) (и не square) тогда я могу вручную настроить размер окна, чтобы получить то, что я хочу, но как я могу сделать это автоматически?

Answer 1

Опция для получения квадратных сюжетов состоит в том, чтобы установить параметры субплота так, чтобы результирующие субплоты автоматически корректировались как квадратные. Это немного связано, потому что все поля и расстояния должны быть приняты во внимание.

import matplotlib.pyplot as plt

f, (ax1, ax2) = plt.subplots(1, 2)
x = [1 , 4 , 6]
y1 = [4, 7, 9]
y2 = [20, 89, 99]

def square_subplots(fig):
    rows, cols = ax1.get_subplotspec().get_gridspec().get_geometry()
    l = fig.subplotpars.left
    r = fig.subplotpars.right
    t = fig.subplotpars.top
    b = fig.subplotpars.bottom
    wspace = fig.subplotpars.wspace
    hspace = fig.subplotpars.hspace
    figw,figh = fig.get_size_inches()

    axw = figw*(r-l)/(cols+(cols-1)*wspace)
    axh = figh*(t-b)/(rows+(rows-1)*hspace)
    axs = min(axw,axh)
    w = (1-axs/figw*(cols+(cols-1)*wspace))/2.
    h = (1-axs/figh*(rows+(rows-1)*hspace))/2.
    fig.subplots_adjust(bottom=h, top=1-h, left=w, right=1-w)

ax1.plot(x, y1, 'o')
ax2.plot(x, y2, 'o')

#f.tight_layout() # optionally call tight_layout first
square_subplots(f)

plt.show()

Преимущество здесь в том, чтобы иметь возможность свободно масштабировать и автоматически масштабировать. Недостатком является то, что после изменения размера фигуры размеры подзаговоров больше не являются квадратными. Чтобы преодолеть этот недостаток, можно дополнительно зарегистрировать обратный вызов при изменении размера фигуры.

import matplotlib.pyplot as plt

f, (ax1, ax2) = plt.subplots(1, 2)
x = [1 , 4 , 6]
y1 = [4, 7, 9]
y2 = [20, 89, 99]

class SquareSubplots():
    def __init__(self, fig):
        self.fig = fig
        self.ax = self.fig.axes[0]
        self.figw,self.figh = 0,0
        self.params = [self.fig.subplotpars.left,
                       self.fig.subplotpars.right,
                       self.fig.subplotpars.top,
                       self.fig.subplotpars.bottom,
                       self.fig.subplotpars.wspace,
                       self.fig.subplotpars.hspace]
        self.rows, self.cols = self.ax.get_subplotspec().get_gridspec().get_geometry()
        self.update(None)
        self.cid = self.fig.canvas.mpl_connect('resize_event', self.update)


    def update(self, evt):
        figw,figh = self.fig.get_size_inches()
        if self.figw != figw or self.figh != figh:
            self.figw = figw; self.figh = figh
            l,r,t,b,wspace,hspace = self.params
            axw = figw*(r-l)/(self.cols+(self.cols-1)*wspace)
            axh = figh*(t-b)/(self.rows+(self.rows-1)*hspace)
            axs = min(axw,axh)
            w = (1-axs/figw*(self.cols+(self.cols-1)*wspace))/2.
            h = (1-axs/figh*(self.rows+(self.rows-1)*hspace))/2.
            self.fig.subplots_adjust(bottom=h, top=1-h, left=w, right=1-w)
            self.fig.canvas.draw_idle()

s = SquareSubplots(f)

ax1.plot(x, y1, 'o')
ax2.plot(x, y2, 'o')

plt.show()

Answer 2

Нет такого волшебного слова, как "квадрат", но вы можете поиграть с set_aspect после того, как вы установите ограничения (отбросьте квадратные линии, которые влияют на значения осей):

...
ax1.set_aspect(1.5)
ax2.set_aspect(0.095)
plt.show()

Я просто поиграл, чтобы получить значения выше:

Вы можете вычислить это, разделив x-диапазон на y-диапазон - оценка 8/5 для ax1и 8/85 для ax2, просто посмотрев на графики, но вы можете использовать точные значения, чтобы быть точным:

xr1=ax1.get_xlim()
yr1=ax1.get_ylim()
scale1=(xr1[1]-xr1[0])/(yr1[1]-yr1[0])
ax1.set_aspect(scale1) #1.454545..., almost 1.5!