Как вы рассчитываете среднее значение для набора циклических данных?
Я хочу рассчитать среднее значение для набора циклических данных. Например, у меня может быть несколько примеров чтения компаса. Проблема, конечно, заключается в том, как справиться с циклом. Тот же алгоритм может быть полезен для циферблата.
Фактический вопрос более сложен - что означает статистика на сфере или в алгебраическом пространстве, которое "оборачивается", например, аддитивная группа mod n. Ответ может быть не уникальным, например, среднее значение 359 градусов и 1 градус может быть 0 градусов или 180, но статистически 0 выглядит лучше.
Это реальная проблема программирования для меня, и я пытаюсь сделать так, чтобы она не выглядела просто математической проблемой.
30 ответов
Вычислить единичные векторы по углам и взять угол их среднего.
Этот вопрос подробно рассматривается в книге: "Статистика по сферам", Джеффри С. Уотсон, Конспект лекций по математическим наукам Университета Арканзаса, 1983 г., John Wiley & Sons, Inc., как упомянуто по адресу http://catless.ncl.ac.uk/Risks/7.44.html Брюса Карша.
Хороший способ оценить средний угол A из набора угловых измерений a[i] 0<=i
sum_i_from_1_to_N sin(a[i])
a = arctangent ---------------------------
sum_i_from_1_to_N cos(a[i])
Метод, данный starblue, эквивалентен в вычислительном отношении, но его причины более ясны и, вероятно, программно более эффективны, а также хорошо работают в нулевом случае, так что слава ему.
Теперь предмет более подробно рассматривается в Википедии, а также в других областях, таких как дробные части.
Я вижу проблему - например, если у вас угол 45'и угол 315', "естественное" среднее значение будет 180', но на самом деле вы хотите получить значение 0'.
Я думаю, что Starblue на что-то. Просто вычислите (x, y) декартовы координаты для каждого угла и сложите полученные результирующие векторы. Угловое смещение конечного вектора должно быть вашим требуемым результатом.
x = y = 0
foreach angle {
x += cos(angle)
y += sin(angle)
}
average_angle = atan2(y, x)
Сейчас я игнорирую, что направление по компасу начинается с севера и идет по часовой стрелке, тогда как "нормальные" декартовы координаты начинаются с нуля вдоль оси X, а затем идут против часовой стрелки. Математика должна работать одинаково независимо.
В ОСОБЫХ СЛУЧАЯХ ДВУХ УГЛОВ:
Ответ ( (a + b) mod 360) / 2 НЕПРАВИЛЬНЫЙ. Для углов 350 и 2 ближайшая точка - 356, а не 176.
Единичный вектор и триггерные решения могут быть слишком дорогими.
Что я получил от небольшого переделывания:
diff = ( ( a - b + 180 + 360 ) mod 360 ) - 180
angle = (360 + b + ( diff / 2 ) ) mod 360
- 0, 180 -> 90 (два ответа для этого: это уравнение берет ответ по часовой стрелке от a)
- 180, 0 -> 270 (см. Выше)
- 180, 1 -> 90,5
- 1, 180 -> 90,5
- 20, 350 -> 5
- 350, 20 -> 5 (все последующие примеры тоже меняются местами)
- 10, 20 -> 15
- 350, 2 -> 356
- 359,0 -> 359,5
- 180, 180 -> 180
Акб прав, что эти векторные решения нельзя считать истинными средними значениями углов, они являются только средними значениями единичных векторов. Тем не менее, предложенное решение Акба не кажется математически обоснованным.
Следующее является решением, которое математически получено из цели минимизации (angle[i] - avgAngle)^2 (где разница корректируется при необходимости), что делает его истинным средним арифметическим углов.
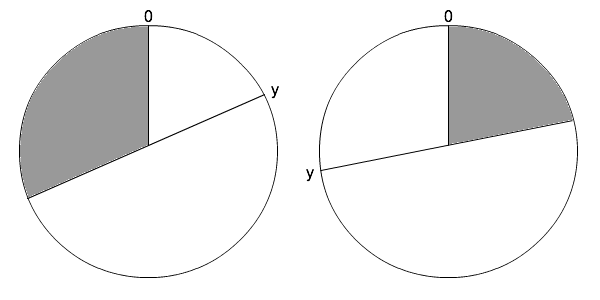
Во-первых, нам нужно посмотреть, в каких именно случаях разница между углами отличается от разницы между их обычными числами. Рассмотрим углы x и y, если y >= x - 180 и y <= x + 180, то мы можем напрямую использовать разность (xy). В противном случае, если первое условие не выполняется, мы должны использовать (y+360) в расчете вместо y. Соответственно, если второе условие не выполнено, тогда мы должны использовать (y-360) вместо y. Поскольку уравнение кривой мы минимизируем только изменения в точках, где эти неравенства изменяются с истинного на ложное или наоборот, мы можем разделить полный диапазон [0,360) на набор сегментов, разделенных этими точками. Затем нам нужно только найти минимум каждого из этих сегментов, а затем минимум каждого сегмента, который является средним.
Вот изображение, демонстрирующее, где возникают проблемы при расчете угловых разностей. Если х лежит в серой области, тогда возникнет проблема.
Чтобы минимизировать переменную, в зависимости от кривой, мы можем взять производную того, что мы хотим минимизировать, и затем мы найдем точку поворота (где производная = 0).
Здесь мы применим идею минимизации квадрата разности, чтобы вывести общую формулу среднего арифметического: sum(a[i])/n. Кривая y = sum((a[i]-x)^2) может быть минимизирована следующим образом:
y = sum((a[i]-x)^2)
= sum(a[i]^2 - 2*a[i]*x + x^2)
= sum(a[i]^2) - 2*x*sum(a[i]) + n*x^2
dy\dx = -2*sum(a[i]) + 2*n*x
for dy/dx = 0:
-2*sum(a[i]) + 2*n*x = 0
-> n*x = sum(a[i])
-> x = sum(a[i])/n
Теперь примените его к кривым с нашими скорректированными отличиями:
b = подмножество a, где правильная (угловая) разница a[i]-x c = подмножество a, где правильная (угловая) разница (a[i]-360)-x cn = размер c d = подмножество a, где правильная (угловая) разница (a[i]+360)-x dn = размер d
y = sum((b[i]-x)^2) + sum(((c[i]-360)-b)^2) + sum(((d[i]+360)-c)^2)
= sum(b[i]^2 - 2*b[i]*x + x^2)
+ sum((c[i]-360)^2 - 2*(c[i]-360)*x + x^2)
+ sum((d[i]+360)^2 - 2*(d[i]+360)*x + x^2)
= sum(b[i]^2) - 2*x*sum(b[i])
+ sum((c[i]-360)^2) - 2*x*(sum(c[i]) - 360*cn)
+ sum((d[i]+360)^2) - 2*x*(sum(d[i]) + 360*dn)
+ n*x^2
= sum(b[i]^2) + sum((c[i]-360)^2) + sum((d[i]+360)^2)
- 2*x*(sum(b[i]) + sum(c[i]) + sum(d[i]))
- 2*x*(360*dn - 360*cn)
+ n*x^2
= sum(b[i]^2) + sum((c[i]-360)^2) + sum((d[i]+360)^2)
- 2*x*sum(x[i])
- 2*x*360*(dn - cn)
+ n*x^2
dy/dx = 2*n*x - 2*sum(x[i]) - 2*360*(dn - cn)
for dy/dx = 0:
2*n*x - 2*sum(x[i]) - 2*360*(dn - cn) = 0
n*x = sum(x[i]) + 360*(dn - cn)
x = (sum(x[i]) + 360*(dn - cn))/n
Одного этого недостаточно для получения минимума, хотя он работает для нормальных значений, у которых есть неограниченный набор, поэтому результат определенно будет лежать в пределах диапазона набора и, следовательно, будет действительным. Нам нужен минимум в пределах диапазона (определяемого сегментом). Если минимум меньше нижней границы нашего сегмента, то минимум этого сегмента должен находиться на нижней границе (поскольку у квадратичных кривых есть только одна точка поворота), а если минимум больше верхней границы нашего сегмента, то минимум сегмента находится на верхняя граница. После того, как у нас есть минимум для каждого сегмента, мы просто находим тот, который имеет наименьшее значение для того, что мы минимизируем (sum((b[i]-x)^2) + sum(((c[i]-360)-b)^2) + сумма (((d[i]+360)-c)^2)).
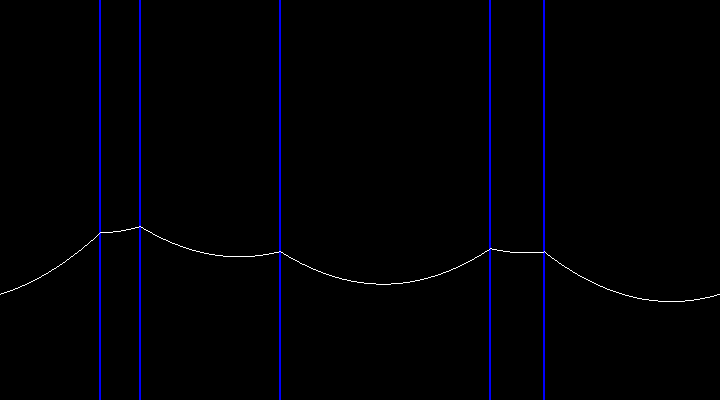
Вот изображение кривой, которое показывает, как оно изменяется в точках, где x=(a[i]+180)%360. Набор данных находится под вопросом {65,92,230,320,250}.
Вот реализация алгоритма на Java, включающая некоторые оптимизации, его сложность составляет O(nlogn). Его можно уменьшить до O(n), если заменить сортировку, основанную на сравнении, сортировкой, не основанной на сравнении, например радикальной сортировкой.
static double varnc(double _mean, int _n, double _sumX, double _sumSqrX)
{
return _mean*(_n*_mean - 2*_sumX) + _sumSqrX;
}
//with lower correction
static double varlc(double _mean, int _n, double _sumX, double _sumSqrX, int _nc, double _sumC)
{
return _mean*(_n*_mean - 2*_sumX) + _sumSqrX
+ 2*360*_sumC + _nc*(-2*360*_mean + 360*360);
}
//with upper correction
static double varuc(double _mean, int _n, double _sumX, double _sumSqrX, int _nc, double _sumC)
{
return _mean*(_n*_mean - 2*_sumX) + _sumSqrX
- 2*360*_sumC + _nc*(2*360*_mean + 360*360);
}
static double[] averageAngles(double[] _angles)
{
double sumAngles;
double sumSqrAngles;
double[] lowerAngles;
double[] upperAngles;
{
List<Double> lowerAngles_ = new LinkedList<Double>();
List<Double> upperAngles_ = new LinkedList<Double>();
sumAngles = 0;
sumSqrAngles = 0;
for(double angle : _angles)
{
sumAngles += angle;
sumSqrAngles += angle*angle;
if(angle < 180)
lowerAngles_.add(angle);
else if(angle > 180)
upperAngles_.add(angle);
}
Collections.sort(lowerAngles_);
Collections.sort(upperAngles_,Collections.reverseOrder());
lowerAngles = new double[lowerAngles_.size()];
Iterator<Double> lowerAnglesIter = lowerAngles_.iterator();
for(int i = 0; i < lowerAngles_.size(); i++)
lowerAngles[i] = lowerAnglesIter.next();
upperAngles = new double[upperAngles_.size()];
Iterator<Double> upperAnglesIter = upperAngles_.iterator();
for(int i = 0; i < upperAngles_.size(); i++)
upperAngles[i] = upperAnglesIter.next();
}
List<Double> averageAngles = new LinkedList<Double>();
averageAngles.add(180d);
double variance = varnc(180,_angles.length,sumAngles,sumSqrAngles);
double lowerBound = 180;
double sumLC = 0;
for(int i = 0; i < lowerAngles.length; i++)
{
//get average for a segment based on minimum
double testAverageAngle = (sumAngles + 360*i)/_angles.length;
//minimum is outside segment range (therefore not directly relevant)
//since it is greater than lowerAngles[i], the minimum for the segment
//must lie on the boundary lowerAngles[i]
if(testAverageAngle > lowerAngles[i]+180)
testAverageAngle = lowerAngles[i];
if(testAverageAngle > lowerBound)
{
double testVariance = varlc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,i,sumLC);
if(testVariance < variance)
{
averageAngles.clear();
averageAngles.add(testAverageAngle);
variance = testVariance;
}
else if(testVariance == variance)
averageAngles.add(testAverageAngle);
}
lowerBound = lowerAngles[i];
sumLC += lowerAngles[i];
}
//Test last segment
{
//get average for a segment based on minimum
double testAverageAngle = (sumAngles + 360*lowerAngles.length)/_angles.length;
//minimum is inside segment range
//we will test average 0 (360) later
if(testAverageAngle < 360 && testAverageAngle > lowerBound)
{
double testVariance = varlc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,lowerAngles.length,sumLC);
if(testVariance < variance)
{
averageAngles.clear();
averageAngles.add(testAverageAngle);
variance = testVariance;
}
else if(testVariance == variance)
averageAngles.add(testAverageAngle);
}
}
double upperBound = 180;
double sumUC = 0;
for(int i = 0; i < upperAngles.length; i++)
{
//get average for a segment based on minimum
double testAverageAngle = (sumAngles - 360*i)/_angles.length;
//minimum is outside segment range (therefore not directly relevant)
//since it is greater than lowerAngles[i], the minimum for the segment
//must lie on the boundary lowerAngles[i]
if(testAverageAngle < upperAngles[i]-180)
testAverageAngle = upperAngles[i];
if(testAverageAngle < upperBound)
{
double testVariance = varuc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,i,sumUC);
if(testVariance < variance)
{
averageAngles.clear();
averageAngles.add(testAverageAngle);
variance = testVariance;
}
else if(testVariance == variance)
averageAngles.add(testAverageAngle);
}
upperBound = upperAngles[i];
sumUC += upperBound;
}
//Test last segment
{
//get average for a segment based on minimum
double testAverageAngle = (sumAngles - 360*upperAngles.length)/_angles.length;
//minimum is inside segment range
//we test average 0 (360) now
if(testAverageAngle < 0)
testAverageAngle = 0;
if(testAverageAngle < upperBound)
{
double testVariance = varuc(testAverageAngle,_angles.length,sumAngles,sumSqrAngles,upperAngles.length,sumUC);
if(testVariance < variance)
{
averageAngles.clear();
averageAngles.add(testAverageAngle);
variance = testVariance;
}
else if(testVariance == variance)
averageAngles.add(testAverageAngle);
}
}
double[] averageAngles_ = new double[averageAngles.size()];
Iterator<Double> averageAnglesIter = averageAngles.iterator();
for(int i = 0; i < averageAngles_.length; i++)
averageAngles_[i] = averageAnglesIter.next();
return averageAngles_;
}
Среднее арифметическое набора углов может не совпадать с вашим интуитивным представлением о том, каким должно быть среднее значение. Например, среднее арифметическое для набора {179,179,0,181,181} равно 216 (и 144). Ответ, о котором вы сразу подумаете, вероятно, равен 180, однако хорошо известно, что среднее арифметическое сильно зависит от значений ребер. Вы также должны помнить, что углы не являются векторами, как это может показаться привлекательным, когда иногда приходится иметь дело с углами.
Этот алгоритм, конечно, также применим ко всем величинам, которые подчиняются модульной арифметике (с минимальной корректировкой), например, ко времени суток.
Я также хотел бы подчеркнуть, что, хотя это истинное среднее углов, в отличие от векторных решений, это не обязательно означает, что это решение, которое вы должны использовать, среднее значение соответствующих единичных векторов вполне может быть значением, которое вы на самом деле следует использовать.
Я хотел бы поделиться методом, который я использовал с микроконтроллером, который не имел возможностей с плавающей запятой или тригонометрии. Мне все еще нужно было "усреднить" 10 необработанных показаний подшипников, чтобы сгладить вариации.
- Проверьте, находится ли первый подшипник в диапазоне 270-360 или 0-90 градусов (два северных квадранта)
- Если это так, поверните это и все последующие показания на 180 градусов, сохраняя все значения в диапазоне 0 <= подшипник < 360. В противном случае считайте показания по мере их поступления.
- После того, как были сделаны 10 показаний, вычислите среднее числовое значение, предполагая, что не было никакого обхода
- Если вращение на 180 градусов действовало, то поверните рассчитанное среднее значение на 180 градусов, чтобы вернуться к "истинному" азимуту.
Это не идеально; это может сломаться. Мне это сошло с рук в этом случае, потому что устройство вращается очень медленно. Я опубликую это на тот случай, если кто-то другой обнаружит, что работает в подобных условиях.
В питоне, с углами между [-180, 180)
def add_angles(a, b):
return (a + b + 180) % 360 - 180
def average_angles(a, b):
return add_angles(a, add_angles(-a, b)/2)
Подробности:
Для среднего из двух углов есть два средних значения на 180° друг от друга, но нам может потребоваться более близкое среднее.
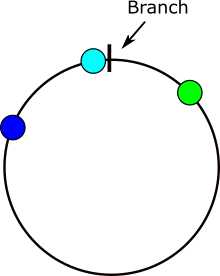
Визуально, среднее значение синего (b) и зеленого (a) значений дает точку размытия:
Углы "окружают" (например, 355 + 10 = 5), но стандартная арифметика игнорирует эту точку ветвления. Однако, если угол b противоположен точке ветвления, то (b + g) / 2 дает ближайший средний показатель: чирную точку.
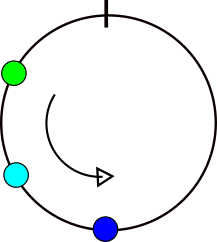
Для любых двух углов мы можем повернуть задачу так, чтобы один из углов был противоположен точке ветвления, выполнить стандартное усреднение, а затем повернуть назад.
Вы должны определить среднее значение более точно. Для конкретного случая двух углов я могу представить два разных сценария:
- "Истинное" среднее, т. Е. (A + b) / 2 % 360.
- Угол, который указывает "между" двумя другими, оставаясь в том же полукруге, например, для 355 и 5, это будет 0, а не 180. Чтобы сделать это, вам нужно проверить, больше ли разница между двумя углами, чем 180 или нет. Если это так, увеличьте меньший угол на 360, прежде чем использовать приведенную выше формулу.
Однако я не понимаю, как можно обобщить вторую альтернативу на случай более двух углов.
Как и все средние, ответ зависит от выбора метрики. Для данной метрики M среднее значение некоторых углов a_k в [-pi,pi] для k в [1,N] является тем углом a_M, который минимизирует сумму квадратов расстояний d^2_M(a_M,a_k). Для взвешенного среднего можно просто включить в сумму веса w_k (такие, что sum_k w_k = 1). То есть,
a_M = arg min_x sum_k w_k d ^ 2_M (x, a_k)
Два общих выбора метрики - это метрики Фробениуса и Римана. Для метрики Фробениуса существует прямая формула, которая соответствует обычному понятию среднего значения в круговой статистике. См. "Средства и усреднение в группе вращений", Maher Moakher, SIAM Journal по матричному анализу и приложениям, том 24, выпуск 1, 2002, для получения более подробной информации.
http://link.aip.org/link/?SJMAEL/24/1/1
Вот функция для GNU Octave 3.2.4, которая выполняет вычисления:
function ma=meanangleoct(a,w,hp,ntype)
% ma=meanangleoct(a,w,hp,ntype) returns the average of angles a
% given weights w and half-period hp using norm type ntype
% Ref: "Means and Averaging in the Group of Rotations",
% Maher Moakher, SIAM Journal on Matrix Analysis and Applications,
% Volume 24, Issue 1, 2002.
if (nargin<1) | (nargin>4), help meanangleoct, return, end
if isempty(a), error('no measurement angles'), end
la=length(a); sa=size(a);
if prod(sa)~=la, error('a must be a vector'); end
if (nargin<4) || isempty(ntype), ntype='F'; end
if ~sum(ntype==['F' 'R']), error('ntype must be F or R'), end
if (nargin<3) || isempty(hp), hp=pi; end
if (nargin<2) || isempty(w), w=1/la+0*a; end
lw=length(w); sw=size(w);
if prod(sw)~=lw, error('w must be a vector'); end
if lw~=la, error('length of w must equal length of a'), end
if sum(w)~=1, warning('resumming weights to unity'), w=w/sum(w); end
a=a(:); % make column vector
w=w(:); % make column vector
a=mod(a+hp,2*hp)-hp; % reduce to central period
a=a/hp*pi; % scale to half period pi
z=exp(i*a); % U(1) elements
% % NOTA BENE:
% % fminbnd can get hung up near the boundaries.
% % If that happens, shift the input angles a
% % forward by one half period, then shift the
% % resulting mean ma back by one half period.
% X=fminbnd(@meritfcn,-pi,pi,[],z,w,ntype);
% % seems to work better
x0=imag(log(sum(w.*z)));
X=fminbnd(@meritfcn,x0-pi,x0+pi,[],z,w,ntype);
% X=real(X); % truncate some roundoff
X=mod(X+pi,2*pi)-pi; % reduce to central period
ma=X*hp/pi; % scale to half period hp
return
%%%%%%
function d2=meritfcn(x,z,w,ntype)
x=exp(i*x);
if ntype=='F'
y=x-z;
else % ntype=='R'
y=log(x'*z);
end
d2=y'*diag(w)*y;
return
%%%%%%
% % test script
% %
% % NOTA BENE: meanangleoct(a,[],[],'R') will equal mean(a)
% % when all abs(a-b) < pi/2 for some value b
% %
% na=3, a=sort(mod(randn(1,na)+1,2)-1)*pi;
% da=diff([a a(1)+2*pi]); [mda,ndx]=min(da);
% a=circshift(a,[0 2-ndx]) % so that diff(a(2:3)) is smallest
% A=exp(i*a), B1=expm(a(1)*[0 -1; 1 0]),
% B2=expm(a(2)*[0 -1; 1 0]), B3=expm(a(3)*[0 -1; 1 0]),
% masimpl=[angle(mean(exp(i*a))) mean(a)]
% Bsum=B1+B2+B3; BmeanF=Bsum/sqrt(det(Bsum));
% % this expression for BmeanR should be correct for ordering of a above
% BmeanR=B1*(B1'*B2*(B2'*B3)^(1/2))^(2/3);
% mamtrx=real([[0 1]*logm(BmeanF)*[1 0]' [0 1]*logm(BmeanR)*[1 0]'])
% manorm=[meanangleoct(a,[],[],'F') meanangleoct(a,[],[],'R')]
% polar(a,1+0*a,'b*'), axis square, hold on
% polar(manorm(1),1,'rs'), polar(manorm(2),1,'gd'), hold off
% Meanangleoct Version 1.0
% Copyright (C) 2011 Alphawave Research, robjohnson@alphawaveresearch.com
% Released under GNU GPLv3 -- see file COPYING for more info.
%
% Meanangle is free software: you can redistribute it and/or modify
% it under the terms of the GNU General Public License as published by
% the Free Software Foundation, either version 3 of the License, or (at
% your option) any later version.
%
% Meanangle is distributed in the hope that it will be useful, but
% WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
% General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with this program. If not, see `http://www.gnu.org/licenses/'.
Вот полное решение: (входной сигнал представляет собой массив азимутов в градусах (0-360)
public static int getAvarageBearing(int[] arr)
{
double sunSin = 0;
double sunCos = 0;
int counter = 0;
for (double bearing : arr)
{
bearing *= Math.PI/180;
sunSin += Math.sin(bearing);
sunCos += Math.cos(bearing);
counter++;
}
int avBearing = INVALID_ANGLE_VALUE;
if (counter > 0)
{
double bearingInRad = Math.atan2(sunSin/counter, sunCos/counter);
avBearing = (int) (bearingInRad*180f/Math.PI);
if (avBearing<0)
avBearing += 360;
}
return avBearing;
}
Если кто-то ищет решение для этого на JavaScript, я перевел пример, приведенный на странице википедии " Среднее значение круговых величин" (о котором также упоминалось в ответе Ника), в код JavaScript/NodeJS с помощью библиотеки mathjs.
Если ваши углы указаны в градусах:
const maths = require('mathjs');
getAverageDegrees = (array) => {
let arrayLength = array.length;
let sinTotal = 0;
let cosTotal = 0;
for (let i = 0; i < arrayLength; i++) {
sinTotal += maths.sin(array[i] * (maths.pi / 180));
cosTotal += maths.cos(array[i] * (maths.pi / 180));
}
let averageDirection = maths.atan(sinTotal / cosTotal) * (180 / maths.pi);
if (cosTotal < 0) {
averageDirection += 180;
} else if (sinTotal < 0) {
averageDirection += 360;
}
return averageDirection;
}
Это решение сработало для меня очень хорошо, чтобы найти среднее направление из набора направлений компаса. Я тестировал это на большом диапазоне направленных данных (0-360 градусов), и он кажется очень надежным.
В качестве альтернативы, если ваши углы указаны в радианах:
const maths = require('mathjs');
getAverageRadians = (array) => {
let arrayLength = array.length;
let sinTotal = 0;
let cosTotal = 0;
for (let i = 0; i < arrayLength; i++) {
sinTotal += maths.sin(array[i]);
cosTotal += maths.cos(array[i]);
}
let averageDirection = maths.atan(sinTotal / cosTotal);
if (cosTotal < 0) {
averageDirection += 180;
} else if (sinTotal < 0) {
averageDirection += 360;
}
return averageDirection;
}
Надеюсь, эти решения будут полезны тем, кто сталкивается с аналогичной мне проблемой программирования.
По-английски:
- Создайте второй набор данных со всеми углами, смещенными на 180.
- Возьмите дисперсию обоих наборов данных.
- Возьмите среднее значение для набора данных с наименьшей дисперсией.
- Если это среднее значение из смещенного набора, то снова сдвиньте ответ на 180.
В питоне:
#Numpy NX1 массив углов
if np.var(A) < np.var((A-180)%360):
average = np.average(A)
else:
average = (np.average((A-180)%360)+180)%360
Основываясь на ответе Альнитака, я написал метод Java для вычисления среднего значения нескольких углов:
Если ваши углы в радианах:
public static double averageAngleRadians(double... angles) {
double x = 0;
double y = 0;
for (double a : angles) {
x += Math.cos(a);
y += Math.sin(a);
}
return Math.atan2(y, x);
}
Если ваши углы в градусах:
public static double averageAngleDegrees(double... angles) {
double x = 0;
double y = 0;
for (double a : angles) {
x += Math.cos(Math.toRadians(a));
y += Math.sin(Math.toRadians(a));
}
return Math.toDegrees(Math.atan2(y, x));
}
Я бы пошел вектор, используя комплексные числа. Мой пример в Python, который имеет встроенные комплексные числа:
import cmath # complex math
def average_angle(list_of_angles):
# make a new list of vectors
vectors= [cmath.rect(1, angle) # length 1 for each vector
for angle in list_of_angles]
vector_sum= sum(vectors)
# no need to average, we don't care for the modulus
return cmath.phase(vector_sum)
Обратите внимание, что Python не должен создавать временный новый список векторов, все вышеперечисленное можно сделать за один шаг; Я просто выбрал этот способ, чтобы приблизить псевдокод, применимый и к другим языкам.
Вот полное решение C++:
#include <vector>
#include <cmath>
double dAngleAvg(const vector<double>& angles) {
auto avgSin = double{ 0.0 };
auto avgCos = double{ 0.0 };
static const auto conv = double{ 0.01745329251994 }; // PI / 180
static const auto i_conv = double{ 57.2957795130823 }; // 180 / PI
for (const auto& theta : angles) {
avgSin += sin(theta*conv);
avgCos += cos(theta*conv);
}
avgSin /= (double)angles.size();
avgCos /= (double)angles.size();
auto ret = double{ 90.0 - atan2(avgCos, avgSin) * i_conv };
if (ret<0.0) ret += 360.0;
return fmod(ret, 360.0);
}
Он принимает углы в виде вектора двойных значений и возвращает среднее значение просто как двойной. Углы должны быть в градусах, и, конечно, среднее значение также в градусах.
Вот идея: постройте среднее значение итеративно, всегда вычисляя среднее значение углов, которые находятся ближе всего друг к другу, сохраняя вес.
Другая идея: найти самый большой зазор между заданными углами. Найдите точку, которая делит ее пополам, а затем выберите противоположную точку на круге в качестве контрольного нуля, чтобы вычислить среднее значение.
Вот полностью арифметическое решение с использованием скользящих средних и заботой о нормализации значений. Это быстро и дает правильные ответы, если все углы находятся на одной стороне круга (в пределах 180° друг от друга).
Это математически эквивалентно добавлению смещения, которое сдвигает значения в диапазон (0, 180), вычисляет среднее значение и затем вычитает смещение.
Комментарии описывают, какой диапазон может принимать конкретное значение в любой момент времени.
// angles have to be in the range [0, 360) and within 180° of each other.
// n >= 1
// returns the circular average of the angles int the range [0, 360).
double meanAngle(double* angles, int n)
{
double average = angles[0];
for (int i = 1; i<n; i++)
{
// average: (0, 360)
double diff = angles[i]-average;
// diff: (-540, 540)
if (diff < -180)
diff += 360;
else if (diff >= 180)
diff -= 360;
// diff: (-180, 180)
average += diff/(i+1);
// average: (-180, 540)
if (average < 0)
average += 360;
else if (average >= 360)
average -= 360;
// average: (0, 360)
}
return average;
}
Представим эти углы точками на окружности круга.
Можно ли предположить, что все эти точки попадают на одну и ту же половину круга? (В противном случае не существует очевидного способа определения "среднего угла". Подумайте о двух точках на диаметре, например, 0 и 180 градусов - это среднее значение 90 или 270 градусов? Что происходит, когда у нас 3 или больше равномерно распределить точки?)
С этим предположением мы выбираем произвольную точку на этом полукруге в качестве "начала координат" и измеряем заданный набор углов относительно этого начала координат (назовем это "относительным углом"). Обратите внимание, что относительный угол имеет абсолютное значение строго менее 180 градусов. Наконец, возьмите среднее значение этих относительных углов, чтобы получить желаемый средний угол (относительно нашего происхождения, конечно).
Что ж, я очень опоздал на вечеринку, но подумал, что добавлю свои 2 цента, потому что не смог найти окончательного ответа. В конце я реализовал следующую Java-версию метода Mitsuta, которая, я надеюсь, предоставляет простое и надежное решение. В частности, стандартное отклонение обеспечивает как дисперсию измерения, так и, если sd == 90, указывает, что входные углы приводят к неоднозначному среднему значению.
РЕДАКТИРОВАТЬ: На самом деле я понял, что моя первоначальная реализация может быть еще более упрощена, на самом деле, на удивление просто, учитывая все разговоры и тригонометрию, происходящие в других ответах.
/**
* The Mitsuta method
*
* @param angles Angles from 0 - 360
* @return double array containing
* 0 - mean
* 1 - sd: a measure of angular dispersion, in the range [0..360], similar to standard deviation.
* Note if sd == 90 then the mean can also be its inverse, i.e. 360 == 0, 300 == 60.
*/
public static double[] getAngleStatsMitsuta(double... angles) {
double sum = 0;
double sumsq = 0;
for (double angle : angles) {
if (angle >= 180) {
angle -= 360;
}
sum += angle;
sumsq += angle * angle;
}
double mean = sum / angles.length;
return new double[]{mean <= 0 ? 360 + mean: mean, Math.sqrt(sumsq / angles.length - (mean * mean))};
}
... и для всех вас (Java) гиков, вы можете использовать вышеупомянутый подход, чтобы получить средний угол в одной строке.
Arrays.stream(angles).map(angle -> angle<180 ? angle: (angle-360)).sum() / angles.length;
(Просто хочу поделиться своей точкой зрения из теории оценивания или статистического вывода)
Задача Nimble состоит в том, чтобы получить MMSE^ оценку набора углов, но это один из вариантов, чтобы найти "усредненное" направление; Можно также найти оценку MMAE^ или некоторую другую оценку, чтобы быть "усредненным" направлением, и это зависит от вашей количественной погрешности измерения метрики направления; или, в более общем смысле, в теории оценки - определение функции стоимости.
^ MMSE / MMAE соответствует минимальному среднему квадрату / абсолютной ошибке.
Акб сказал: "Средний угол phi_avg должен иметь свойство, которое sum_i|phi_avg-phi_i|^2 становится минимальным... они что-то усредняют, но не углы"
---- вы количественно определяете ошибки в среднеквадратичном смысле, и это один из наиболее распространенных способов, однако не единственный. Ответ, одобренный большинством людей здесь (т. Е. Сумма векторов единиц и угол результата), на самом деле является одним из разумных решений. Это (может быть доказано) оценка ML, которая служит "усредненным" направлением, которое мы хотим, если направления векторов моделируются как распределение фон Мизеса. Это распределение не является причудливым и представляет собой просто периодически выбираемое распределение из двумерного гассиана. Смотрите уравнение (2.179) в книге Бишопа "Распознавание образов и машинное обучение". Опять же, ни в коем случае это не единственный лучший способ представить "среднее" направление, однако, вполне разумное, имеющее как хорошее теоретическое обоснование, так и простую реализацию.
Нимбл сказал: "Акб прав, что эти векторные решения не могут считаться истинными средними значениями углов, они являются только средним значением единичных векторов"
----это неправда. "Единичные векторные аналоги" раскрывают информацию о направлении вектора. Угол - это величина без учета длины вектора, а единичный вектор - это нечто с дополнительной информацией о том, что длина равна 1. Вы можете определить, что ваш "единичный" вектор имеет длину 2, это на самом деле не имеет значения.
Вы можете увидеть решение и небольшое объяснение по следующей ссылке для ЛЮБОГО языка программирования: https://rosettacode.org/wiki/Averages/Mean_angle
Например, решение C++:
#include<math.h>
#include<stdio.h>
double
meanAngle (double *angles, int size)
{
double y_part = 0, x_part = 0;
int i;
for (i = 0; i < size; i++)
{
x_part += cos (angles[i] * M_PI / 180);
y_part += sin (angles[i] * M_PI / 180);
}
return atan2 (y_part / size, x_part / size) * 180 / M_PI;
}
int
main ()
{
double angleSet1[] = { 350, 10 };
double angleSet2[] = { 90, 180, 270, 360};
double angleSet3[] = { 10, 20, 30};
printf ("\nMean Angle for 1st set : %lf degrees", meanAngle (angleSet1, 2));
printf ("\nMean Angle for 2nd set : %lf degrees", meanAngle (angleSet2, 4));
printf ("\nMean Angle for 3rd set : %lf degrees\n", meanAngle (angleSet3, 3));
return 0;
}
Выход:
Mean Angle for 1st set : -0.000000 degrees
Mean Angle for 2nd set : -90.000000 degrees
Mean Angle for 3rd set : 20.000000 degrees
Или решение Matlab:
function u = mean_angle(phi)
u = angle(mean(exp(i*pi*phi/180)))*180/pi;
end
mean_angle([350, 10])
ans = -2.7452e-14
mean_angle([90, 180, 270, 360])
ans = -90
mean_angle([10, 20, 30])
ans = 20.000
Там нет ни одного "правильного ответа". Я рекомендую прочитать книгу KV Mardia и PE Jupp, "Direction Statistics" (Wiley, 1999), для тщательного анализа.
Вот некоторый Java-код для усреднения углов, я думаю, он достаточно надежный.
public static double getAverageAngle(List<Double> angles)
{
// r = right (0 to 180 degrees)
// l = left (180 to 360 degrees)
double rTotal = 0;
double lTotal = 0;
double rCtr = 0;
double lCtr = 0;
for (Double angle : angles)
{
double norm = normalize(angle);
if (norm >= 180)
{
lTotal += norm;
lCtr++;
} else
{
rTotal += norm;
rCtr++;
}
}
double rAvg = rTotal / Math.max(rCtr, 1.0);
double lAvg = lTotal / Math.max(lCtr, 1.0);
if (rAvg > lAvg + 180)
{
lAvg += 360;
}
if (lAvg > rAvg + 180)
{
rAvg += 360;
}
double rPortion = rAvg * (rCtr / (rCtr + lCtr));
double lPortion = lAvg * (lCtr / (lCtr + rCtr));
return normalize(rPortion + lPortion);
}
public static double normalize(double angle)
{
double result = angle;
if (angle >= 360)
{
result = angle % 360;
}
if (angle < 0)
{
result = 360 + (angle % 360);
}
return result;
}
Вы можете использовать эту функцию в Matlab:
function retVal=DegreeAngleMean(x)
len=length(x);
sum1=0;
sum2=0;
count1=0;
count2=0;
for i=1:len
if x(i)<180
sum1=sum1+x(i);
count1=count1+1;
else
sum2=sum2+x(i);
count2=count2+1;
end
end
if (count1>0)
k1=sum1/count1;
end
if (count2>0)
k2=sum2/count2;
end
if count1>0 && count2>0
if(k2-k1 >= 180)
retVal = ((sum1+sum2)-count2*360)/len;
else
retVal = (sum1+sum2)/len;
end
elseif count1>0
retVal = k1;
else
retVal = k2;
end
Средний угол phi_avg должен обладать свойством того, что sum_i|phi_avg-phi_i|^2 становится минимальным, где разница должна быть в [-Pi, Pi) (потому что это может быть короче, если идти наоборот!). Это легко достигается путем нормализации всех входных значений до [0, 2Pi), сохранения среднего значения phi_run и выбора нормализации |phi_i-phi_run| к [-Pi, Pi) (путем добавления или вычитания 2Pi). Большинство предложений выше делают что-то еще, что не имеет этого минимального свойства, то есть они усредняют что-то, но не углы.
Функция Python:
from math import sin,cos,atan2,pi
import numpy as np
def meanangle(angles,weights=0,setting='degrees'):
'''computes the mean angle'''
if weights==0:
weights=np.ones(len(angles))
sumsin=0
sumcos=0
if setting=='degrees':
angles=np.array(angles)*pi/180
for i in range(len(angles)):
sumsin+=weights[i]/sum(weights)*sin(angles[i])
sumcos+=weights[i]/sum(weights)*cos(angles[i])
average=atan2(sumsin,sumcos)
if setting=='degrees':
average=average*180/pi
return average
В то время как ответ starblue дает угол среднего единичного вектора, можно расширить понятие среднего арифметического на углы, если принять, что может быть более одного ответа в диапазоне от 0 до 2* пи (или от 0° до 360°). Например, среднее значение 0° и 180° может составлять либо 90°, либо 270°.
Среднее арифметическое имеет свойство быть единственным значением с минимальной суммой квадратов расстояний до входных значений. Расстояние вдоль единичного круга между двумя единичными векторами можно легко рассчитать как обратный косинус их точечного произведения. Если мы выберем единичный вектор путем минимизации суммы квадрата обратного косинуса точечного произведения нашего вектора и каждого входного единичного вектора, то мы получим эквивалентное среднее значение. Опять же, имейте в виду, что в исключительных случаях может быть два или более минимума.
Эту концепцию можно распространить на любое количество измерений, поскольку расстояние вдоль единичной сферы можно рассчитать точно так же, как расстояние вдоль единичной окружности - обратный косинус точечного произведения двух единичных векторов.
Для кругов мы могли бы решить для этого среднего значения несколькими способами, но я предлагаю следующий алгоритм O(n^2) (углы указаны в радианах, и я избегаю вычисления единичных векторов):
var bestAverage = -1
double minimumSquareDistance
for each a1 in input
var sumA = 0;
for each a2 in input
var a = (a2 - a1) mod (2*pi) + a1
sumA += a
end for
var averageHere = sumA / input.count
var sumSqDistHere = 0
for each a2 in input
var dist = (a2 - averageHere + pi) mod (2*pi) - pi // keep within range of -pi to pi
sumSqDistHere += dist * dist
end for
if (bestAverage < 0 OR sumSqDistHere < minimumSquareDistance) // for exceptional cases, sumSqDistHere may be equal to minimumSquareDistance at least once. In these cases we will only find one of the averages
minimumSquareDistance = sumSqDistHere
bestAverage = averageHere
end if
end for
return bestAverage
Если все углы находятся в пределах 180° друг от друга, то мы могли бы использовать более простой алгоритм O(n)+O(sort) (снова используя радианы и избегая использования единичных векторов):
sort(input)
var largestGapEnd = input[0]
var largestGapSize = (input[0] - input[input.count-1]) mod (2*pi)
for (int i = 1; i < input.count; ++i)
var gapSize = (input[i] - input[i - 1]) mod (2*pi)
if (largestGapEnd < 0 OR gapSize > largestGapSize)
largestGapSize = gapSize
largestGapEnd = input[i]
end if
end for
double sum = 0
for each angle in input
var a2 = (angle - largestGapEnd) mod (2*pi) + largestGapEnd
sum += a2
end for
return sum / input.count
Чтобы использовать градусы, просто замените pi на 180. Если вы планируете использовать больше измерений, вам, скорее всего, придется использовать итерационный метод для вычисления среднего значения.
Альнитак имеет правильное решение. Решение Ника Фортескью функционально одинаково.
Для особого случая, где
( sum(x_component) = 0.0 && sum(y_component) = 0.0) // например, 2 угла 10 и 190. градусов.
используйте 0, 0 градусов в качестве суммы
В вычислительном отношении вы должны проверить этот случай, так как atan2 (0, 0) не определено и приведет к ошибке.
Проблема чрезвычайно проста. 1. Убедитесь, что все углы находятся в диапазоне от -180 до 180 градусов. 2. a Добавьте все неотрицательные углы, возьмите их среднее и СЧИТАЙТЕ сколько 2. б. Добавьте все отрицательные углы, возьмите их среднее и СЧИТАЙТЕ сколько. 3. Возьмите разницу pos_average минус neg_average. Если разница больше 180, то измените разницу на 360 минус разница. В противном случае просто измените знак различия. Обратите внимание, что разница всегда неотрицательна. Average_Angle равен pos_average плюс разница, умноженная на "вес", отрицательное число, деленное на сумму отрицательного и положительного числа
Я решил проблему с помощью ответа от @David_Hanak. Как он заявляет:
Угол, который указывает "между" двумя другими, оставаясь в том же полукруге, например, для 355 и 5, это будет 0, а не 180. Чтобы сделать это, вам нужно проверить, больше ли разница между двумя углами, чем 180 или нет. Если это так, увеличьте меньший угол на 360, прежде чем использовать приведенную выше формулу.
Поэтому я вычислил среднее значение по всем углам. А затем все углы, которые меньше этого, увеличивают их на 360. Затем пересчитайте среднее значение, сложив их все и разделив на их длину.
float angleY = 0f;
int count = eulerAngles.Count;
for (byte i = 0; i < count; i++)
angleY += eulerAngles[i].y;
float averageAngle = angleY / count;
angleY = 0f;
for (byte i = 0; i < count; i++)
{
float angle = eulerAngles[i].y;
if (angle < averageAngle)
angle += 360f;
angleY += angle;
}
angleY = angleY / count;
Работает отлично.