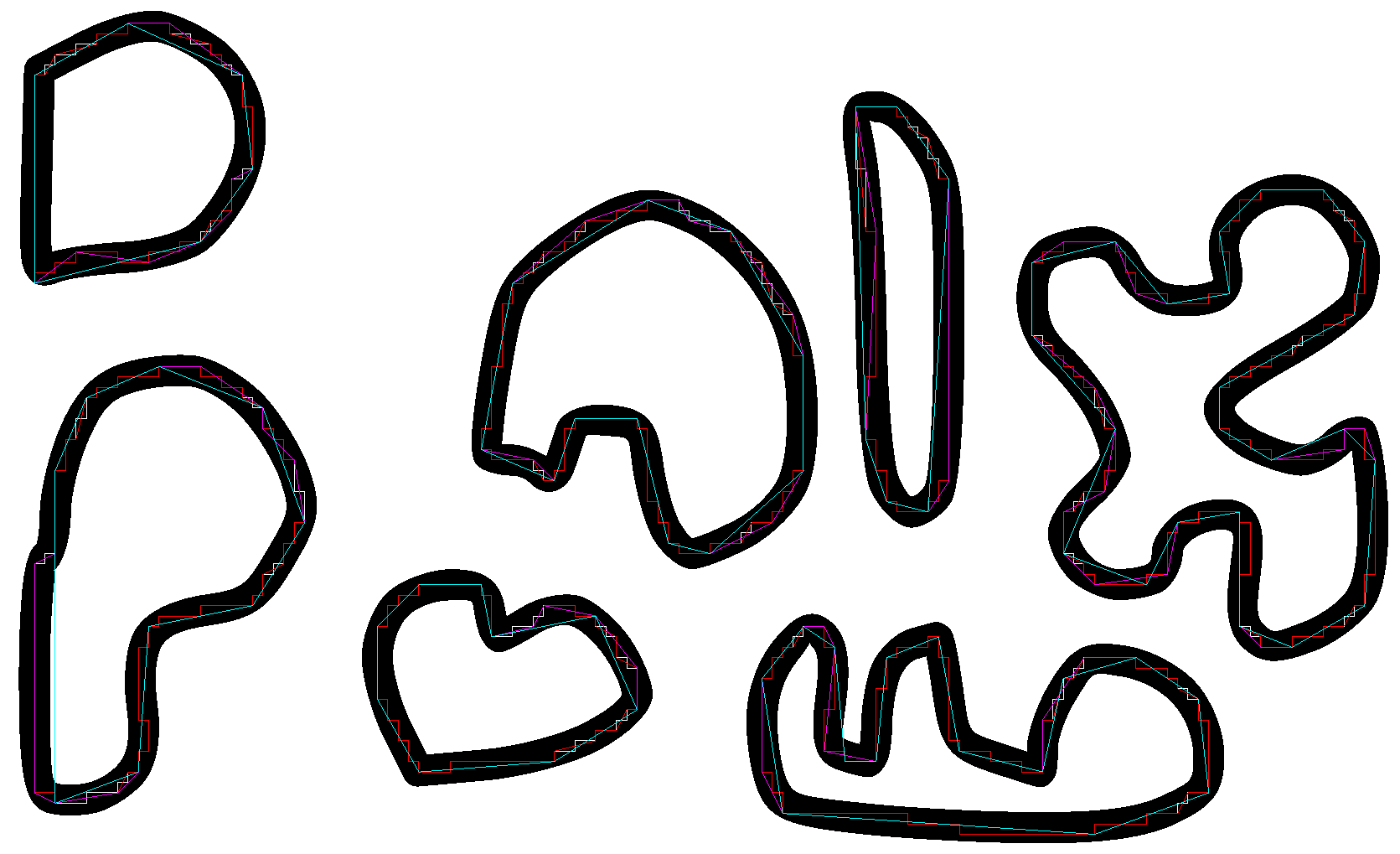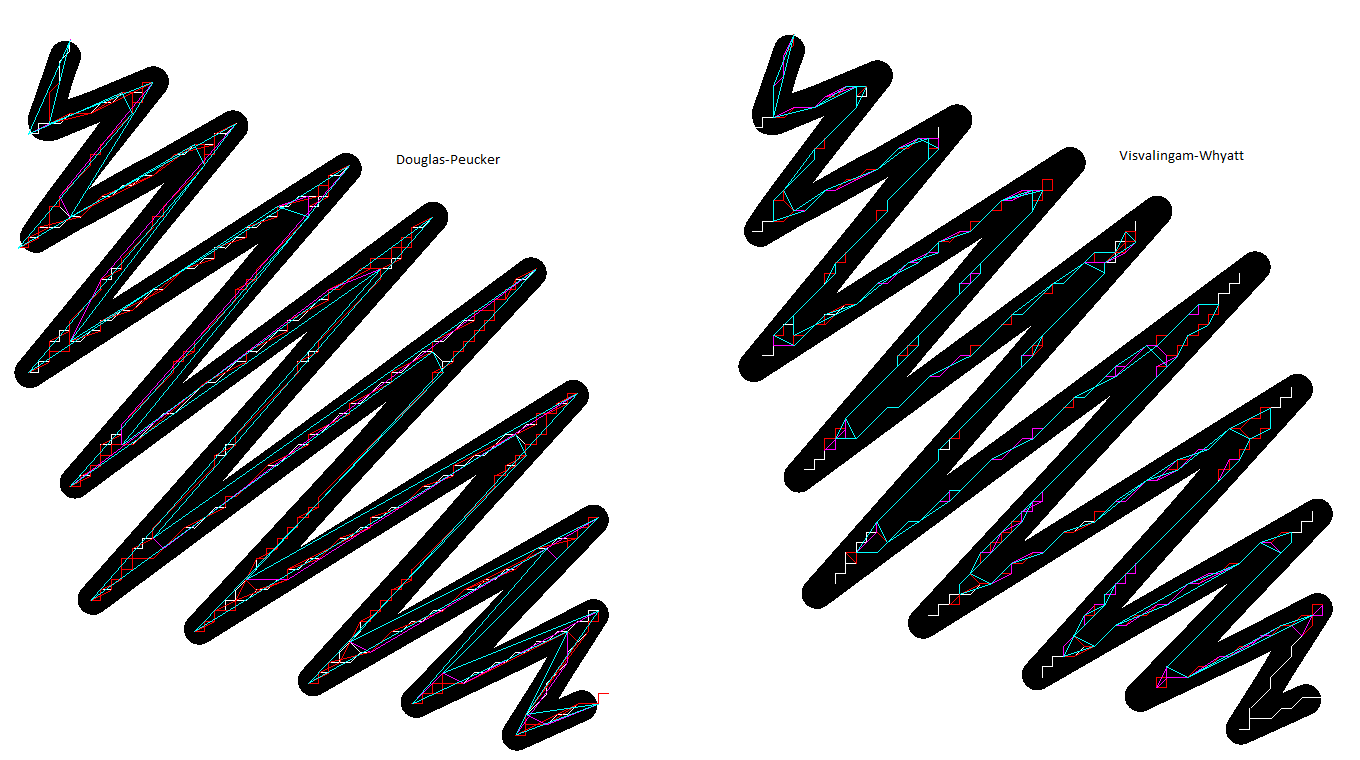Алгоритм упрощения линии: Висвалингам - Дуглас-Пейкер

Я пытаюсь реализовать алгоритм Siplification. Основные два алгоритма, которые я нашел, это Ramer-Douglas-Peucker: https://en.wikipedia.org/wiki/Ramer%E2%80%93Douglas%E2%80%93Peucker_algorithm и Visvalingam-Whyatt: https://bost.ocks.org/mike/simplify/ В настоящее время я запускаю несколько их симуляций на matlab, чтобы определить, какие из них лучше отвечают моим потребностям.

Основная цель алгоритма - симплифицировать многоугольники на карте. Мой вход - это полигон \ полилиния и порог ошибки-эпсилона.

Мне нужно, чтобы упрощенный полигон был как можно ближе к оригиналу, и у меня нет требования по количеству точек, которые нужно сохранить.

У меня возникают трудности при сравнении двух алгоритмов, потому что: epsilon для RDP - это расстояние, а epsilon для VW - это область. Мне нужна помощь в понимании того, как сравнивать два алгоритма. что может дать мне меньше очков, чтобы удержаться в пределах порога?

Источник

1 ответ

Мне нужно, чтобы упрощенный полигон был как можно ближе к оригиналу, и у меня нет требования по количеству точек, которые нужно сохранить.

Метод DP даст вам лучшее восприятие с меньшим количеством точек - как его контрольный параметр, то есть допуск на расстояние определяется вашим требованием "как можно ближе".

Сказав это, масштаб всего многоугольника или облака точек относительно размеров в пикселях будет иметь большее влияние для меньших изображений. Упражнение ниже может дать вам представление о том, как работают два алгоритма.

Вот некоторые сравнения, которые я провел между Visvalingam-Whyatt и Ramer-Douglas-Peucker для нескольких контуров, содержащихся в растровом изображении размером около 100x100. Изображения представляют собой скриншоты с 10-кратным увеличением контуров.

(вы можете загрузить изображения, чтобы оценить разницу в производительности)

Результаты метода Visvalingam-Whyatt: любезно предоставлено реализацией Зака ​​на github, портированной на типы данных opencv. 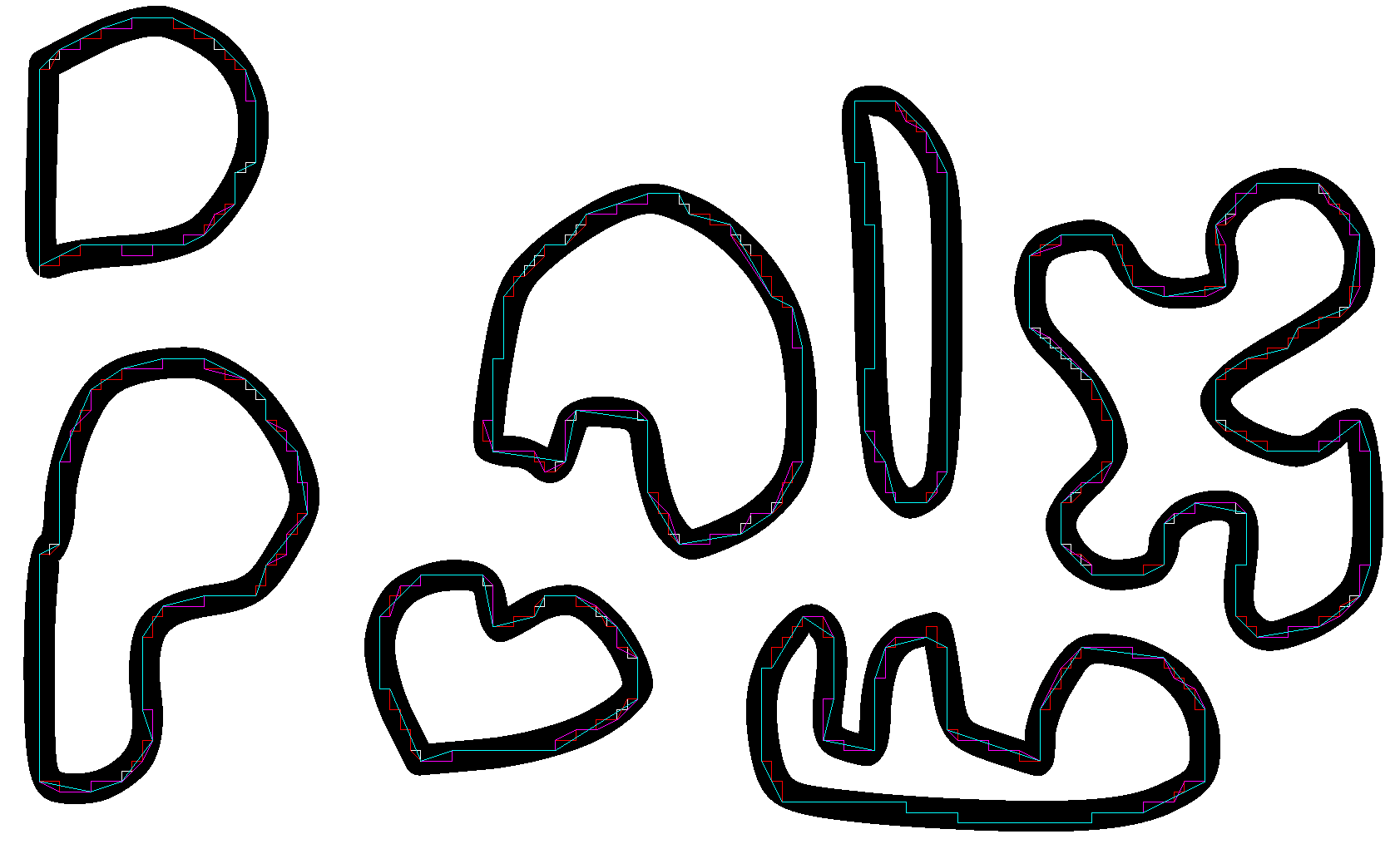Упрощение VSV - с допусками 0,1 (белый), 0,5 (красный), 1 (пурпурный), 2 (голубой

Упрощение VSV - с допусками 0,55 (белый), 0,4 (красный), 0,25 (пурпурный), 0,15 (голубой)

VSV - точка снижения t:% допуска. это напрямую определяет n = t * orig / 100. n - итоговое количество баллов

orig 88: [n=47 for t=0.55], [n=34 for t=0.4], [n=20 for t=0.25], [n=12 for t=0.15]
orig 133: [n=72 for t=0.55], [n=52 for t=0.4], [n=32 for t=0.25], [n=18 for t=0.15]
orig 118: [n=63 for t=0.55], [n=46 for t=0.4], [n=28 for t=0.25], [n=16 for t=0.15]
orig 107: [n=57 for t=0.55], [n=41 for t=0.4], [n=25 for t=0.25], [n=15 for t=0.15]
orig 107: [n=57 for t=0.55], [n=41 for t=0.4], [n=25 for t=0.25], [n=15 for t=0.15]
orig 268: [n=146 for t=0.55], [n=106 for t=0.4], [n=65 for t=0.25], [n=39 for t=0.15]
orig 158: [n=85 for t=0.55], [n=62 for t=0.4], [n=38 for t=0.25], [n=22 for t=0.15]
orig 158: [n=85 for t=0.55], [n=62 for t=0.4], [n=38 for t=0.25], [n=22 for t=0.15]
orig 109: [n=58 for t=0.55], [n=42 for t=0.4], [n=26 for t=0.25], [n=15 for t=0.15]
orig 192: [n=104 for t=0.55], [n=75 for t=0.4], [n=46 for t=0.25], [n=27 for t=0.15]
orig 132: [n=71 for t=0.55], [n=51 for t=0.4], [n=31 for t=0.25], [n=18 for t=0.15]
orig 89: [n=47 for t=0.55], [n=34 for t=0.4], [n=21 for t=0.25], [n=12 for t=0.15]
orig 110: [n=59 for t=0.55], [n=42 for t=0.4], [n=26 for t=0.25], [n=15 for t=0.15]
orig 40: [n=20 for t=0.55], [n=14 for t=0.4], [n=8 for t=0.25], [n=4 for t=0.15]

Результаты метода DP с использованием openCV окПолиДП

Упрощение DP - с допусками 0,1 (белый), 0,5 (красный), 1 (пурпурный), 2 (голубой

Дуглас-Пеккер - уменьшение точек t: допуск на расстояние в пикселях => нет прямой корреляции с n - конечное число точек

orig 88: [n=33 for t=0.1], [n=29 for t=0.5], [n=8 for t=1], [n=6 for t=2]
orig 133: [n=57 for t=0.1], [n=45 for t=0.5], [n=12 for t=1], [n=7 for t=2]
orig 118: [n=50 for t=0.1], [n=40 for t=0.5], [n=15 for t=1], [n=8 for t=2]
orig 107: [n=47 for t=0.1], [n=35 for t=0.5], [n=11 for t=1], [n=6 for t=2]
orig 107: [n=30 for t=0.1], [n=24 for t=0.5], [n=8 for t=1], [n=6 for t=2]
orig 268: [n=126 for t=0.1], [n=110 for t=0.5], [n=32 for t=1], [n=23 for t=2]
orig 158: [n=80 for t=0.1], [n=62 for t=0.5], [n=17 for t=1], [n=11 for t=2]
orig 158: [n=66 for t=0.1], [n=52 for t=0.5], [n=16 for t=1], [n=9 for t=2]
orig 109: [n=50 for t=0.1], [n=38 for t=0.5], [n=12 for t=1], [n=9 for t=2]
orig 192: [n=74 for t=0.1], [n=64 for t=0.5], [n=18 for t=1], [n=15 for t=2]
orig 132: [n=58 for t=0.1], [n=45 for t=0.5], [n=14 for t=1], [n=11 for t=2]
orig 89: [n=37 for t=0.1], [n=31 for t=0.5], [n=7 for t=1], [n=6 for t=2]
orig 110: [n=42 for t=0.1], [n=36 for t=0.5], [n=9 for t=1], [n=7 for t=2]
orig 40: [n=18 for t=0.1], [n=15 for t=0.5], [n=9 for t=1], [n=3 for t=2]

Резюме:

  • Оба метода изящно ухудшаются.
  • VSV позволяет указать количество аппроксимируемых точек (в этой реализации)
  • VSV в этой реализации позволяет выбирать несколько приближенных полигонов за один выстрел.
  • VSV сохраняет большое количество выпуклостей на уровне пикселей даже для больших участков кривизны - это может быть нежелательно в некоторых случаях.
  • DP лучше следует за выпуклостями и больше сглаживает перегибы, но жертвуя "близостью".
  • В результате DP дает меньшее количество баллов за один и тот же достигнутый допуск - что в любом случае трудно сравнить между двумя методами
  • DP дает лучшее представление о допуске, так как его линейная спецификация расстояния.

Для моего приложения я предпочитаю контроль, предлагаемый VWV в этой реализации, над возможной эффективностью метода DP.

Но в целом я чувствую, что реализация DP openCVs дает более плавное восприятие.

Хотя мои выводы о производительности VSV основаны только на реализации Зака, я сомневаюсь, что другие реализации дадут характерно разные подмножества полигонов.

[ОБНОВЛЕНИЕ1] Вот сравнение для худшего сценария. DP визуально более приемлемый.

Источник
Другие вопросы по тегам