Среднее значение прогноза и стандартное отклонение

Question

Извиняюсь, если это немного простой вопрос, но я не смог найти ответа на этот вопрос за последнюю неделю, и это сводит меня с ума.

Справочная информация: у меня есть набор данных, который отслеживает вес 5 человек в течение 5 лет. Каждый год у меня есть распределение для веса людей в группе, из которого я вычисляю среднее значение и стандартное отклонение. Данные следующие:

 Year = [2002,2003,2004,2005,2006]
 Weights_2002 = [12, 14, 16, 18, 20]
 Weights_2003 = [14, 16, 18, 20,20]
 Weights_2004 = [16, 18, 20, 22, 18]
 Weights_2005 = [18, 21, 22, 22, 20]
 Weights_2006 = [2, 21, 19, 20, 20]

Вопрос: Как мне спроектировать ежегодное распределение веса для группы на следующие 10 лет? В идеале я хотел бы, чтобы неопределенность в отношении среднего значения увеличивалась с течением времени. Кроме того, я хотел бы, чтобы неопределенность в отношении стандартного отклонения тоже увеличилась. Иными словами, я хотел бы спроектировать распределение веса в будущем, учитывая оба:

1. Естественная дисперсия в данных
2. Растущая неопределенность.

Любая помощь будет с благодарностью. Если кто-нибудь может подсказать, как это сделать в R, это было бы еще лучше.

Спасибо, парни!

Answer 1

Отсутствуют конкретные предложения о том, как использовать инструменты прогнозирования в R, а именно. комментарии к вашему вопросу, вот альтернативный подход, который использует симуляцию Монте-Карло.

Во-первых, немного домашнего хозяйства: стоимость 2 в Weights_2006 это либо опечатка или выброс. Поскольку я не могу сказать, какой, я буду считать, что это выброс и исключить его из анализа.

Во-вторых, вы говорите, что хотите спроектировать дистрибутивы на основе increasing uncertainty, Но ваши данные не поддерживают это.

Year <- c(2002,2003,2004,2005,2006)
W2   <- c(12, 14, 16, 18, 20)
W3   <- c(14, 16, 18, 20,20)
W4   <- c(16, 18, 20, 22, 18)
W5   <- c(18, 21, 22, 22, 20)
W6   <- c(NA, 21, 19, 20, 20)
df   <- rbind(W2,W3,W4,W5,W6)
df   <- data.frame(Year,df)

library(reshape2)   # for melt(...)
library(ggplot2)
data <- melt(df,id="Year", variable.name="Individual",value.name="Weight")
ggplot(data)+
  geom_histogram(aes(x=Weight),binwidth=1,fill="lightgreen",colour="grey50")+
  facet_grid(Year~.)

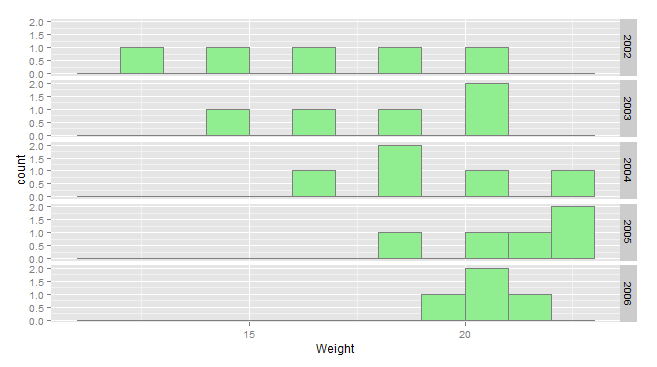
Средний вес увеличивается с течением времени, но дисперсия уменьшается. Взгляд на отдельные временные ряды показывает, почему.

ggplot(data, aes(x=Year, y=Weight, color=Individual))+geom_line()

В общем, вес человека увеличивается линейно со временем (около 2 единиц в год), пока не достигнет 20, когда он перестает расти, но колеблется. Поскольку ваше первоначальное распределение было равномерным, люди с меньшим весом со временем увеличивались, увеличивая среднее значение. Но вес более тяжелых людей перестал расти. Таким образом, распределение "сгруппировано" около 20, что приводит к уменьшению дисперсии. Мы можем видеть это в числах: увеличение среднего значения, уменьшение стандартного отклонения.

smry <- function(x)c(mean=mean(x),sd=sd(x))
aggregate(Weight~Year,data,smry)
#   Year Weight.mean  Weight.sd
# 1 2002  16.0000000  3.1622777
# 2 2003  17.6000000  2.6076810
# 3 2004  18.8000000  2.2803509
# 4 2005  20.6000000  1.6733201
# 5 2006  20.0000000  0.8164966

Мы можем смоделировать это поведение, используя симуляцию Монте-Карло.

set.seed(1)
start <- runif(1000,12,20)
X <- start
result <- X
for (i in 2003:2008){
  X <- X + 2
  X <- ifelse(X<20,X,20) +rnorm(length(X))
  result <- rbind(result,X)
}
result <- data.frame(Year=2002:2008,result)

В этой модели мы начинаем с 1000 человек, чей вес составляет равномерное распределение между 12 и 20, как в ваших данных. На каждом временном шаге мы увеличиваем вес на 2 единицы. Если результат>20, мы обрезаем его до 20. Затем мы добавляем случайный шум, распределенный как N[0,1]. Теперь мы можем построить распределение.

model <- melt(result,id="Year",variable.name="Individual",value.name="Weight")
ggplot(model,aes(x=Weight))+
  geom_histogram(aes(y=..density..),fill="lightgreen",colour="grey50",bins=20)+
  stat_density(geom="line",colour="blue")+
  geom_vline(data=aggregate(Weight~Year,model,mean), aes(xintercept=Weight), colour="red", size=2, linetype=2)+
  facet_grid(Year~.,scales="free")

Красные столбики показывают средний вес каждого года.

Если вы считаете, что естественное изменение веса человека со временем увеличивается, используйте N[0,sigma] как погрешность в модели, с sigma увеличивается с Year, Проблема в том, что в ваших данных нет ничего, что могло бы это поддержать.